
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
ВАЖНО!!! Все пиццы подаются на горячих тарелках (приблизительно 80 оС) !!! Это делается для того, чтобы на столе у гостей пицца как можно дольше сохраняла температуру. 2 страница
|
|
|
|

1.2. Щелчком левой кнопки мыши выберите команду меню «Проводник»; в левом окне Проводника выберите рабочий логический диск (например, диск D):
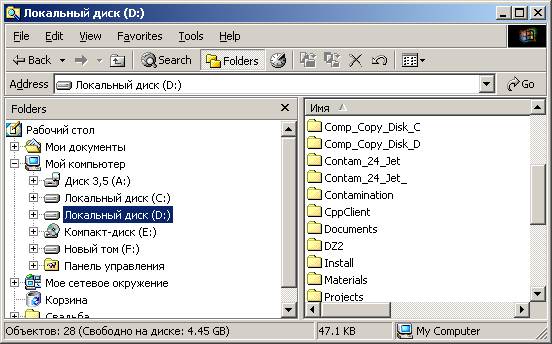
1.3. В правом окне Проводника вызовите контекстное меню
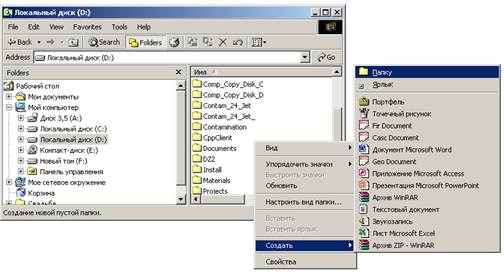
1.4. Выберите команду «Создать / Папку» и наберите имя создаваемой папки (например, Lab1)
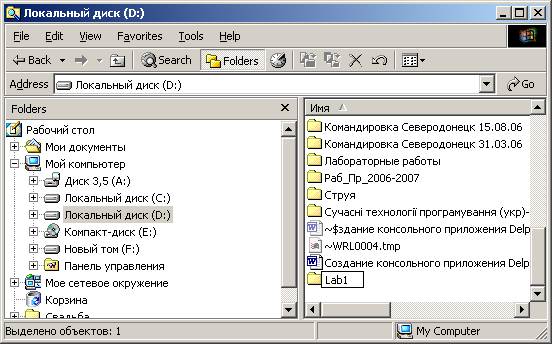
2.1. Командой меню «Пуск / Borland Delphi 7 / Delphi 7» (или аналогичной командой) запустите интегрированную среду программирования Delphi
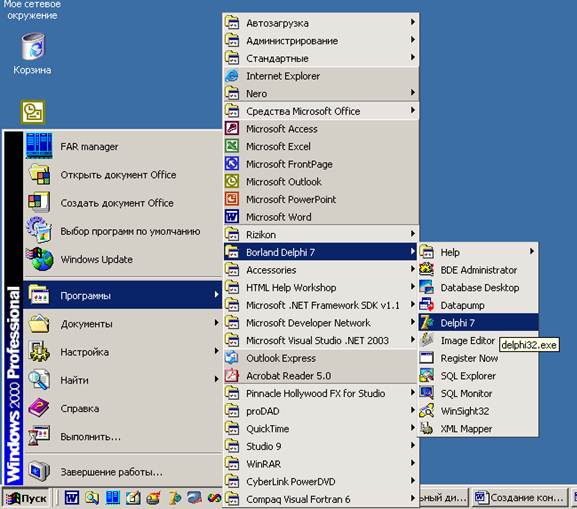
2.2. В появившемся основном окне Delphi выберите команду меню «File / New / Other…»
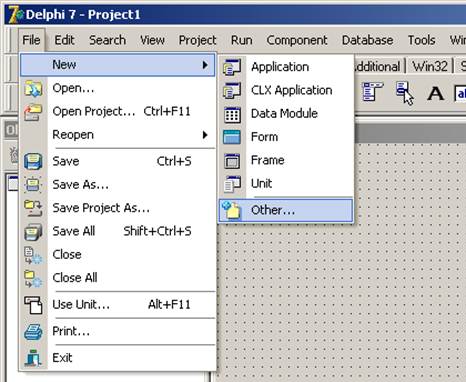
2.3. В окне «New Items» выберите пиктограмму мастера создания консольного приложения «Console Application» и нажмите кнопку «ОК»
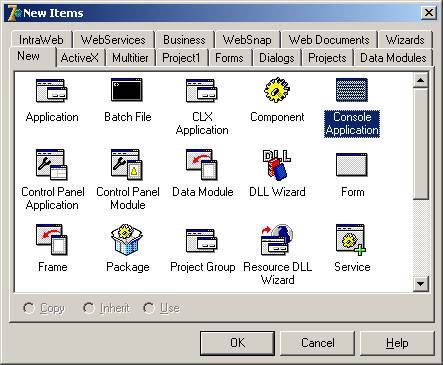
2.4. Появится окно редактора консольного приложения

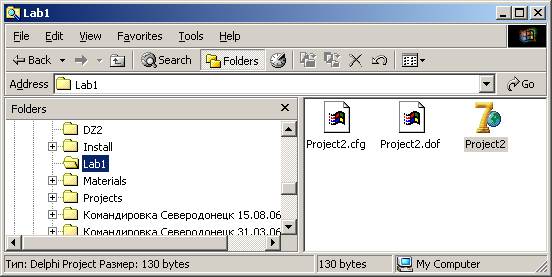
2.5. Сохраните файлы проекта в раннее созданную папку Lab1 с помощью команды основного меню «File / Save Project As…»
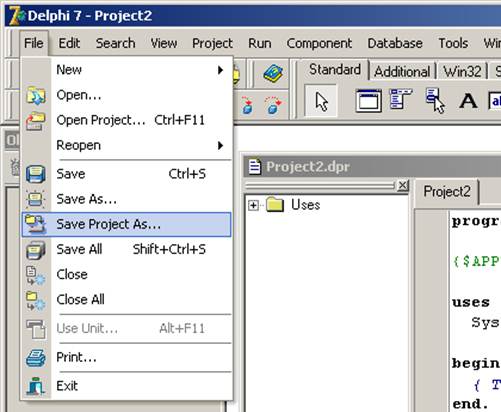
2.6. В окне «Save Project As» с помощью списка «Папка» перейти в папку проекта Lab1 и нажать кнопку «Сохранить»
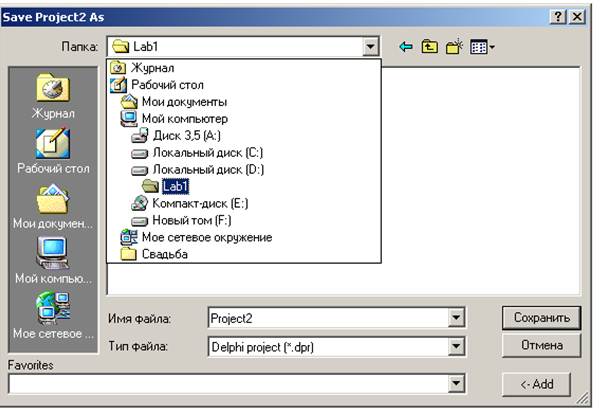
2.7. В результате файлы проекта Project2 будут сохранены в папку Lab1, и Вы в дальнейшем сможете легко отыскать проект на жестком диске для продолжения работы с ним, скопировать папку на дискету для переноса проекта на другой компьютер и т.д.
3.1. Внесите необходимые изменения в текст консольного приложения. Например, выполняемые операторы помещаются вместо комментария {TODO…}. Выведем сообщение в окно консоли с помощью процедуры WriteLn. Вызов процедуры ReadLn можно использовать для задержки окна консоли на экране.
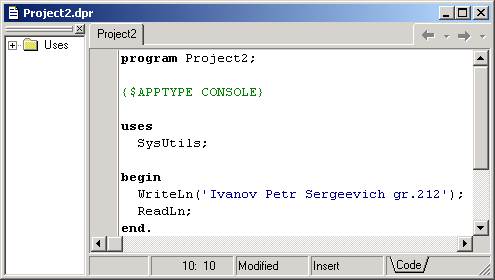
3.2. Директива компилятора {$APPTYPE CONSOLE} свидетельствует о типе нашего приложения и ее необходимо оставить без изменений.
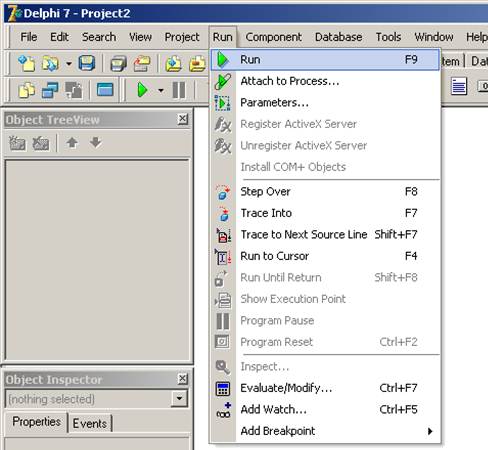
4.1. Командой меню «Run / Run» (горячая клавиша F9) запустите приложение на выполнение.
4.2. В результате запускаются компилятор (синтаксический анализ текста) и редактор связей (подключение стандартных модулей) для построения выполняемого файла. Если ошибки отсутствуют, то приложение выполняется, и появляется консольное окно с результатами расчета:
4.3. Для уменьшения расхода краски при печати можно инвертировать цвета, используя стандартную программу Paint.
4.4. Вставьте из буфера обмена Clipboard результаты расчета (Shift-Insert).
4.5. Инвертируйте цвета командой «Рисунок \ Обратить цвета»
4.6. В результате получим следующий рисунок
4.7. Скопируйте изображение в буфер обмена (Ctrl-Insert) и вставьте в отчет (Shift-Insert)/
4.8. При наличии ошибок в тексте программы ход компиляции и построения выполняемого файла будет остановлен. В этом случае необходимо исправить ошибки и повторить пункт 4.1.
4.9. Консольное окно можно скопировать в память Clipboard (комбинация клавиш Alt-PrtSc) для внесения в текст отчета о лабораторной работе в редакторе Word (Alt-Shift или Ctrl-V).
4.10. Завершите выполнение консольного приложения нажатием клавиши «Enter» (при активном окне консоли).
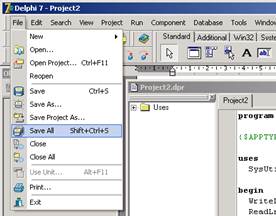
4.11. Сохраните все файлы проекта командой меню «File / Save All»
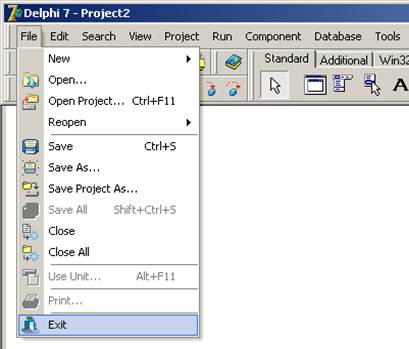
4.12. Завершите работу интегрированной среды разработки программного обеспечения Delphi командой меню «File / Exit»
4.13. Сохраните папку с файлами проекта на дискету
Задания для контрольной работы
для заочного отделения.
1. Вычислить пределы
а. 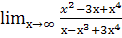 ; б.
; б. 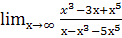 ; в.
; в. 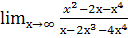 ;
;
г. 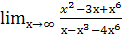 ; д.
; д. 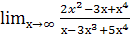 ; е.
; е. 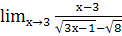 ;
;
ж. 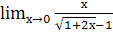 ; з.
; з. 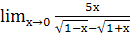 ; и.
; и. 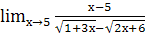 ;
;
к. 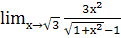 ; л.
; л. 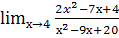 ; м.
; м. 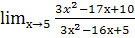 ;
;
н. 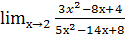 ; о.
; о. 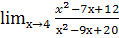 ;
; 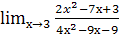
2. Вычислить производные функций
а. 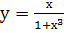 ; б.
; б. 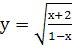 ; в.
; в. 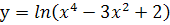 ; г.
; г. 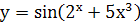 ;
;
д. 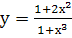 ;е.
;е. 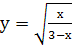 ; ж.
; ж. 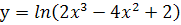 ; з.
; з. 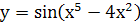 ;
;
и. 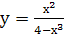 ;к.
;к. 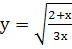 ; л.
; л. 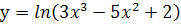 ; м.
; м. 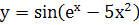 ;
;
н. 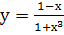 ;о.
;о.  ;п.
;п. 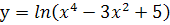 ; р.
; р. 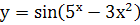
3. Вычислить интеграл
а. 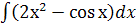 ; б.
; б. 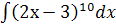 ; в.
; в. 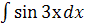 ;
;
г. 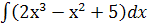 ; д.
; д. 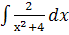 ; е.
; е. 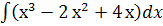 ;
;
ж. 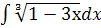 ; з.
; з. 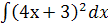 ; и.
; и. 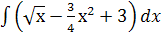
к. 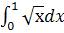 ; л.
; л. 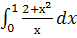 ; м.
; м. 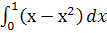 ; н.
; н. 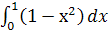 ;
;
о. 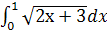
4. Записать комплексное число в тригонометрической форме
а. z = 4 + i;б. z = 3 – 2i; в. 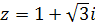 ; г.
; г. 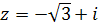 ;
;
д. 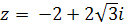 ; е.
; е. 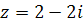 .
.
5. а. В коробке 3 красных, 6 зеленых, 3 синих карандаша. Какова
вероятность взять красный карандаш?
б. В коробке 3 красных, 6 зеленых, 3 синих карандаша. Какова
вероятность взять синий карандаш?
в. В коробке 3 красных, 6 зеленых, 3 синих карандаша. Какова
вероятность взять зеленый карандаш?
г. В коробке 5 красных, 7 зеленых, 3 синих карандаша. Какова
вероятность взять красный карандаш?
д. В коробке 3 красных, 6 зеленых, 3 синих карандаша. Какова
вероятность взять зеленый карандаш?
е. В коробке 3 красных, 6 зеленых, 3 синих карандаша. Какова
вероятность взять синий карандаш?
1.2. Арифметические операции в двоичной системе счисления..............
1.3. Представление отрицательных чисел в двоичной системе счисления
1.4. Кодирование информации …………………………………………….
3.3. Модули памяти …………………………………………………………..
3.4. Карта памяти ……………………………………………………………..
4.3. Дешифратор команд, устройство управления …………………………
4.4. Арифметико-логическое устройство, регистр признаков……………..
4.5. Временные диаграммы работы микропроцессора …………………….
4.6. Работа микропроцессорной системы……………………………………
5.1. Типы команд…………………………………………………………….
5.2. Команды пересылок ……………………………………………………
5.3. Арифметические команды …………………………………………….
5.4. Логические команды ………………………………………………….
5.5. Команды условных и безусловного перехода
Литература........................................................................................................
Введение
Современные ЭВМ используют различные микропроцессорные наборы, которые имеют общие принципы устройства и временные диаграммы работы.
В настоящее время вычислительные мощности процессоров значительно превосходят 8-разрядные процессоры, которые, тем не менее, применяются для реализации микропроцессорных приборов, регуляторов и простых и дешевых контроллеров для управления несложными объектами управления, не требующими высокого быстродействия и имеющими небольшое количество входных и выходных переменных.
В то же время рассмотрение 8-разрядных процессоров позволяет в наглядной и доступной форме рассмотреть и изучить устройство микропроцессора, проследить технологию обработки данных в микропроцессоре.
В учебном пособии основное внимание уделяется вопросам, связанным с устройством и работой микропроцессоров и микроконтроллеров, их программным обеспечением, разработкой программ на языке Ассемблер.
Данное пособие отражает содержание первого модуля дисциплины "Микропроцессорная техника":
· Модуль 1 – Устройство и работа микропроцессора
· Модуль 2 - Устройство и работа микроконтроллера
· Модуль 3 – Программирование микроконтроллеров
· Модуль 4 – Архитектура ЭВМ
· Модуль 5 - Интерфейсы ЭВМ
· Модуль 6 – Курсовая работа
Цель практических занятий – закрепление теоретических знаний и приобретение практических навыков по разработке микропроцессорных систем и их программного обеспечения для решения задач локальной автоматизации.
1. История развития ЭВМ. Системы счисления.
1.1. История развития ЭВМ.
Первые механические вычислительные устройства, счеты, появились еще в античном мире. За 1000 лет до нашей эры появились счеты в Китае и Японии, счеты имели форму бус, укрепленных на специальной раме. Бусы назывались калькулями [1].
Следующим этапом развития вычислительных устройств является создание Б.Паскалем в 1647 г. арифметической машины, которая использовала принцип колес от 0 до 9. В 1966 г. С.Морланд создал суммирующее и вычитающее устройство, а в 1673 г. был изготовлен калькулятор Морланда с умножением чисел.
Лейбниц реализовал вычислительное устройство для умножения и деления чисел.
Отцом вычислительной техники считается Ч.Бэббедж. Он в 1821 г. создал специализированные машины для вычисления разностей между числами, а в начале 30-х годов 19-го века приступил к созданию универсальной вычислительной машины, так как понимал ограниченность разностных машин.
Он первым пришел к заключению, что компьютер должен иметь 5 основных блоков:
- устройство ввода числовой информации (ими были вначале перфокарты Жакара для ткацких станков);
- память для хранения чисел и программ (перфокарта);
- арифметическое устройство;
- устройство управления для контроля над ходом выполнения программы;
- устройство вывода результатов.
В 1890 г. американский ученый Г.Холерит изобрел устройство для анализа результатов переписи населения США, которое было основано на использовании перфокарт с отверстиями, через которые замыкался контакт. На основе реализации данного изобретения в дальнейшем образовалась известная фирма IBM (International Business Machines).
К началу 40-х годов прошлого века стало возможным использовать в качестве элементов схем цифровых машин электролампы и дальнейшее развитие вычислительной техники пошло в направлении использования усилительных элементов, работающих в ключевом режиме с двумя состояниями "да" и "нет".
Развитие средств вычислительной техники развивалось одновременно в нескольких странах. В США, Великобритании, Германии.
В Германии в 1935 г. К.Цузе создает ЭВМ Z1 и патентует ее. В 1941 г. он создает ЭВМ Z3 – двоичный программируемый компьютер, в 1945 г. – первый язык программирования высокого уровня. В дальнейшем его компания влилась в компанию Сименс.
В США в 1943 г. в Гарварде была создана ЭВМ MARK-1, в Великобритании – Colossus-1 – для расшифровки сообщений немецких передатчиков.
Разработка вычислительной техники была стимулирована поставленными задачами науки и техники, которые начали требовать значительного объема расчетных операций, причем их необходимо было выполнять быстро.
Эти задачи были связаны с решением задач управления, а именно управления огнем зенитной артиллерии, расшифровкой радиограмм. В это же время начала зарождаться наука об управлении живыми и неживыми объектами – кибернетика.
Отцом кибернетики считается американский ученый Норберт Винер. Он вместе с мексиканским профессором медицины проанализировал патологии поведения человека при различным заболеваниях нервной системы и сформулировал понятие обратной связи, которое является основополагающим в теории управления.
В 1946 г. Дж.Макли и Дж.Эккерт (Пенсильванский университет) создали ЭВМ ENIAC (Electronic Numerical Integrator and Calculator) – для быстрого вычисления баллистических таблиц для орудий и ракет. Она состояла из 18000 ламп, объем памяти – 20 десятиразрядных чисел, потребление энергии – 150 кВт.
В 1945 г. Дж.фон Нейман приступил к проектированию машины EDVAC (Electronic Discrete Variable Automatic Computer). В проекте этой ЭВМ была реализована концепция управляющей программы, хранимой в памяти машин, а также идея, что с командами можно обращаться так же, как и с информацией, то в этом случае программа может модифицироваться сама в ходе ее исполнения.
В 1947 г. в Кембридже была создана ЭВМ EDSAC (Electronic Delay Storage Automatic Computer). Для нее была создана операционная система.
В 1958 г. появились промышленные образцы транзисторов, которые заменили лампы, что позволило значительно уменьшить габариты вычислительных машин, сократить энергопотребление, повысить их быстродействие. Это привело к созданию машин второго поколения.
В 1965 г. были выпущены интегральные схемы, которые заменили отдельные компоненты ЭВМ, что привело к дальнейшему сокращению габаритов и энергопотребления. Повысилась надежность работы машин, которые были уже машинами третьего поколения. Эти ЭВМ стали применяться для решения задач управления технологическими процессами.
В 1959 г. разработчики фирмы Datapoint (США) разработали первый микропроцессор и предложили фирме Intel реализовать его. Но характеристики этого процессора по быстродействию оказались хуже, чем ожидалось, и фирма Datapoint отказалась от продолжения дальнейших исследований. Фирма Intel тем не менее продолжила исследования, так как уже понесла затраты на разработку, и добилась необходимых результатов. Появился первый микропроцессор Intel 8008 на мировом рынке.
В СССР первые отечественные ЭВМ были созданы под руководством академиков С.А.Лебедева, Ю.А.Базилевского и И.С.Брука. Это малые машины "Наири", "Мир" а также уникальная по быстродействию машина – БЭСМ-6.
1.2.Системы счисления
Развитие вычислительной техники привело к расширению использования различных систем счисления. Обычно используется десятичная система счисления. Однако ее применение для реализации вычислительных процессов с помощью электронных устройств сопряжено с трудностью распознавания десяти различных уровней сигналов, которые бы соответствовали бы различных цифрам. Поэтому в вычислительной технике для реализации вычислений и представления чисел и кодов команд используют двоичную систему счисления, которая имеет две цифры 0 и 1 и для реализации которых в технических устройствах необходимо два уровня сигналов: высоки и низкий, есть сигнал или нет сигнала.
Система счисления определяет правило представления числа из комбинации цифр данной системы счисления. В десятичной системе счисления, которой мы пользуемся повседневно, имеется десять цифр, комбинация которых определяет число. При представлении числа из цифр имеет значение, на каком месте стоит цифра. Место определяет вес данной цифры. Одна и та же цифра может определять количество единиц, десятков, сотен и т.д., все зависит от ее месторасположения в числе.
Такие системы счисления называются позиционными системами счисления по основанию [2]. В этих системах используется конечный набор символов, каждый символ называется цифрой и обозначает некоторое количество. Число различных цифр в наборе называется основанием системы счисления. Чтобы получить какое-либо число, необходимо цифры записать рядом. Относительной позиции цифры в числе ставится в соответствие весовой множитель (коэффициент).
В десятичной системе счисления 10 цифр: 0, 1, … 9. Представление числа в десятичной системе счисления можно представить следующим образом в виде полинома. Например, число 678 будет иметь вид:

Здесь цифра 6 входит с весом 100, цифра 7 – с весом 10, цифра 8 – с весом 1.
В общем виде данное выражение можно представить следующим образом: 
 , (1.1)
, (1.1)
где 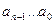 - цифры числа;
- цифры числа;
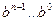 - весовые коэффициенты.
- весовые коэффициенты.
В таблице 1.1 приведены наиболее употребительные системы счисления и их характеристики.
Таблица 1.1, Системы счисления
| Основание | Система счисления | Обозна-чение | Цифровые символы |
| Двоичная | b | 0,1 | |
| Троичная | 0,1,2 | ||
| Четверичная | 0,1,2,3 | ||
| Пятеричная | 0,1,2,3,4 | ||
| Восьмеричная | o | 0,1,2,3,4,5,6,7 | |
| Десятичная | d | 0,1,2,3,4,5,6,7,8,9 | |
| Двенадцатеричная | 0,1,2,3,4,5,6,7,8,9,A,B | ||
| Шестнадцатеричная | h | 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F |
Наибольшее применение в вычислительной технике, наряду с десятичной системой счисления, получили двоичная, восьмеричная и шестнадцатеричная системы счисления. Для различия систем счисления применяют следующие обозначения:
100(10), 100(d) – число представлено в десятичной системе счисления;
100(2), 100(b) - число представлено в двоичной системе счисления;
100(8), 100(o) - число представлено в восьмеричной системе счисления;
100(16), 100(h) - число представлено в шестнадцатеричной системе счисления.
1.3.Двоичная система счисления
Двоичная система счисления использует только две цифры 0 и 1, что позволяет использовать эту систему счисления техническими устройствами для выполнения арифметических операций [3]. Данные технические устройства имеют два устойчивых состояния: включено-выключено, низкий-высокий уровень.
В двоичной системе счисления каждой позиции соответствует определенный вес, который определяется как степень числа 2, так как основание двоичной системы счисления равно 2. Из-за того, что данная система счисления имеет две цифры, разрядность двоичных чисел значительно больше разрядности десятичных чисел.
Представление двоичных чисел и их перевод в десятичное число осуществляется по выражению (1.1)
1011012 = 1*25 + 0*24 + 1*23 + 1*22 + 0*21 + 1*20 =
= 1*32 + 0*16 + 1*8 + 1*4 + 0*2 +1*1 = 4510
При записи двоичного числа каждая позиция занята двоичной цифрой, которая называется битом. Слово бит искусственное, оно произошло как сокращение от двух слов: binary digit (двоичная единица) - bit.
При рассмотрении двоичных чисел пользуются понятиями наименьший значащий бит (самый младший двоичный разряд) и наибольший значащий бит (самый старший двоичный разряд). Обычно двоичное число записывается так, что наибольший значащий бит является крайним слева.
Перевод из десятичной системы в двоичную систему счисления осуществляется следующим образом. Преобразование осуществляется многократным делением десятичного числа на 2. Например, перевод десятичного числа 35 в двоичное число
35:2=17 остаток 1 = a0
17:2=8 остаток 1 = a1
8:2 =4 остаток 0 = a2
4:2 =2 остаток 0 = a3
 2:2 =1 остаток 0 = a4
2:2 =1 остаток 0 = a4
1 = a5
Таким образом, двоичное число будет иметь вид a5a4a3a2a1a0
1000112 = 1*25 + 0*24 + 0*23 + 0*22 + 1*21 + 1*20 =
1*32 + 0*16 + 0*8 + 0*4 + 1*2 +1*1 = 3510
1.4.Шестнадцатеричная система счисления
В шестнадцатеричной системе счисления используются 16 цифр: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F. Шестнадцатеричная система счисления используется как средство сокращенной записи 4-х разрядного двоичного числа. В таблице 1.2 приведены шестнадцатеричные числа и их двоичные и десятичные эквиваленты.
Таблица 1.2
| Шестнадца- теричное число | Двоичное число | Десятичное число | Шестнадца- теричное число | Двоичное число | Десятичное число |
| A | 1A | ||||
| B | 1B | ||||
| C | 1C | ||||
| D | 1D | ||||
| E | 1E | ||||
| F | 1F |
Преобразование двоичного числа в шестнадцатеричное число заключается в том, что биты, начиная с младшего значащего бита, объединяются в группы по четыре. Каждой группе подбирается соответствующий шестнадцатеричный символ. Например, чтобы представить двоичное число 1010101111111012 в виде шестнадцатеричного числа необходимо слева добавить два незначащих нуля с целью формирования битов в группы по четыре: 0010 1010 1111 1101. Заменив каждую группу битов соответствующим шестнадцатеричным символом, получим число 2AFD16.
Данная форма записи намного проще и воспринимается легче, чем двоичная.
Нужно помнить, что шестнадцатеричные числа – это способ представления двоичных чисел, которыми оперирует микропроцессор.
Представление шестнадцатеричного числа в виде двоичного также осуществляется по выражению (1.1).
2AFD16 = 2*163 + A*162 + F*161 + D*160 =
2*4096 + 10*256 + 15*16 + 13*1 =
8192 + 2560 + 240 + 13 = 1100510
101010111111012 = 1*213 + 0*212 + 1*211 +0*210 + 1*29 +0*28 +
+ 1*27 + 1*26 + 1*25 + 1*24 + 1*23 + 1*22 +0*21 +1*20 =
= 8192 + 0 + 2048 + 0 + 512 + 0 + 128 + 64 + 32 + 16 +
+ 8 + 4 + 0 + 1 = 1100510
1.5. Двоичная арифметика
Четыре основные арифметические операции, а именно сложение, вычитание, умножение, деление можно выполнять в позиционной системе счисления с любым основанием.
Сложение двух двоичных чисел
| a | b | a+b |
| 1+1+1 |
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 453; Нарушение авторских прав?; Мы поможем в написании вашей работы!