Сеть Фейштеля

Дополнительные требования

Платформы

Области применения

Стандартный алгоритм шифрования должен быть применим во многих приложениях:

· Шифрование данных. Алгоритм должен быть эффективен при шифровании файлов данных или большого потока данных.

· Создание случайных чисел. Алгоритм должен быть эффективен при создании определенного количества случайных битов.

· Хэширование. Алгоритм должен эффективно преобразовываться в одностороннюю хэш-функцию.

Стандартный алгоритм шифрования должен быть реализован на различных платформах, которые, соответственно, предъявляют различные требования.

· Алгоритм должен эффективно реализовываться на специализированной аппаратуре, предназначенной для выполнения шифрования/дешифрования.

· Большие процессоры. Хотя для наиболее быстрых приложений всегда используется специальная аппаратура, программные реализации применяются чаще. Алгоритм должен допускать эффективную программную реализацию на 32-битных процессорах.

· Процессоры среднего размера. Алгоритм должен работать на микроконтроллерах и других процессорах среднего размера.

· Малые процессоры. Должна существовать возможность реализации алгоритма на смарт-картах, пусть даже с учетом жестких ограничений на используемую память.

Алгоритм шифрования должен, по возможности, удовлетворять некоторым дополнительным требованиям.

· Алгоритм должен быть простым для написания кода, чтобы минимизировать вероятность программных ошибок.

· Алгоритм должен иметь плоское пространство ключей и допускать любую случайную строку битов нужной длины в качестве возможного ключа. Наличие слабых ключей нежелательно.

· Алгоритм должен легко модифицироваться для различных уровней безопасности и удовлетворять как минимальным, так и максимальным требованиям.

· Все операции с данными должны осуществляться над блоками, кратными байту или 32-битному слову.

Блочный алгоритм преобразовывает n-битный блок незашифрованного текста в n-битный блок зашифрованного текста. Число блоков длины n равно 2ⁿ. Для того чтобы преобразование было обратимым, каждый из таких блоков должен преобразовываться в свой уникальный блок зашифрованного текста. При маленькой длине блока такая подстановка плохо скрывает статистические особенности незашифрованного текста. Если блок имеет длину 64 бита, то он уже хорошо скрывает статистические особенности исходного текста. Но в данном случае преобразование текста не может быть произвольным в силу того, что ключом будет являться само преобразование, что исключает эффективную как программную, так и аппаратную реализации.

Наиболее широкое распространение получили сети Фейштеля, так как, с одной стороны, они удовлетворяют всем требованиям к алгоритмам симметричного шифрования, а с другой стороны, достаточно просты и компактны.

Сеть Фейштеля имеет следующую структуру. Входной блок делится на несколько равной длины подблоков, называемых ветвями. В случае, если блок имеет длину 64 бита, используются две ветви по 32 бита каждая. Каждая ветвь обрабатывается независимо от другой, после чего осуществляется циклический сдвиг всех ветвей влево. Такое преобразование выполняется несколько циклов или раундов. В случае двух ветвей каждый раунд имеет структуру, показанную на рисунке:

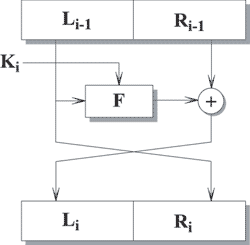
Рис. 2.3. I-ый раунд сети Фейштеля

Функция F называется образующей. Каждый раунд состоит из вычисления функции F для одной ветви и побитового выполнения операции XOR результата F с другой ветвью. После этого ветви меняются местами. Считается, что оптимальное число раундов - от 8 до 32. Важно то, что увеличение количества раундов значительно увеличивает криптостойкость алгоритма. Возможно, эта особенность и повлияла на столь активное распространение сети Фейштеля, так как для большей криптостойкости достаточно просто увеличить количество раундов, не изменяя сам алгоритм. В последнее время количество раундов не фиксируется, а лишь указываются допустимые пределы.

Сеть Фейштеля является обратимой даже в том случае, если функция F не является таковой, так как для дешифрования не требуется вычислять F^-1. Для дешифрования используется тот же алгоритм, но на вход подается зашифрованный текст, и ключи используются в обратном порядке.

В настоящее время все чаще используются различные разновидности сети Фейштеля для 128-битного блока с четырьмя ветвями. Увеличение количества ветвей, а не размерности каждой ветви связано с тем, что наиболее популярными до сих пор остаются процессоры с 32-разрядными словами, следовательно, оперировать 32-разрядными словами эффективнее, чем с 64-разрядными.

Основной характеристикой алгоритма, построенного на основе сети Фейштеля, является функция F. Различные варианты касаются также начального и конечного преобразований. Подобные преобразования, называемые забеливанием (whitening), осуществляются для того, чтобы выполнить начальную рандомизацию входного текста.

Дата добавления: 2014-12-23