Дешифрование. Пятьдесят два 16-битных подключа создаются из 128-битного ключа шифрования следующим образом

Создание подключей

Пятьдесят два 16-битных подключа создаются из 128-битного ключа шифрования следующим образом. Первые восемь подключей, которые обозначим как Z₁, Z₂,..., Z₈, получаются непосредственно из ключа, при этом Z₁ равен первым 16 битам, Z₂ равен следующим 16 битам и т.д. Затем происходит циклический сдвиг ключа влево на 25 битов, и создаются следующие восемь подключей. Эта поцедура повторяется до тех пор, пока не будут созданы все 52 подключа.

Заметим, что каждый первый подключ раунда получен из своего подмножества битов ключа. Если весь ключ обозначить как Z _[1..128], то первыми ключами в восьми раундах будут:

Z₁ = Z _[1..16] Z₂₅ = Z _[76..91]Z₇ = Z _[97..112] Z₃₁ = Z _[44..59]Z₁₃ = Z _[90..105] Z₃₇ = Z _[37..52]Z₁₉ = Z _[83..98] Z₄₃ = Z _[30..45]

Хотя на каждом раунде за исключением первого и восьмого используются только 96 битов подключа, множество битов ключа на каждой итерации не пересекаются, и не существует отношения простого сдвига между подключами разных раундов. Это происходит потому, что на каждом раунде используется только шесть подключей, в то время как при каждой ротации ключа получается восемь подключей.

Процесс дешифрования аналогичен процессу шифрования. Дешифрование состоит в использовании зашифрованного текста в качестве входа в ту же самую структуру IDEA, но с другим набором ключей. Дешифрующие ключи U₁,..., U₅₂ получаются из шифрующих ключей следующим образом:

1. Первые четыре подключа i-ого раунда дешифрования получаются из первых четырех подключей (10-i)-го раунда шифрования, где стадия заключительного преобразования считается 9-м раундом. Первый и четвертый ключи дешифрования эквивалентны мультипликативной инверсии по модулю (2¹⁶ + 1) соответствующих первого и четвертого подключей шифрования. Для раундов со 2 по 8 второй и третий подключи дешифрования эквивалентны аддитивной инверсии по модулю (2¹⁶) соответствующих третьего и второго подключей шифрования. Для раундов 1 и 9 второй и третий подключи дешифрования эквивалентны аддитивной инверсии по модулю (2¹⁶) соответствующих второго и третьего подключей шифрования.

2. Для первых восьми раундов последние два подключа i раунда дешифрования эквивалентны последним двум подключам (9 - i) раунда шифрования.

Для мультипликативной инверсии используется нотация Z_j^-1, т.е.:

Z_j • Z_j^-1 =1 mod (2¹⁶ + 1)

Так как 2¹⁶ + 1 является простым числом, каждое ненулевое целое Z_j 2¹⁶ имеет уникальную мультипликативную инверсию по модулю (2¹⁶ + 1). Для аддитивной инверсии используется нотация (-Z_j), таким образом, мы имеем: -Z_j + Z_j = 0 mod (2¹⁶)

Для доказательства того, что алгоритм дешифрования с соответствующими подключами имеет корректный результат, рассмотрим одновременно процессы шифрования и дешифрования. Каждый из восьми раундов разбит на две стадии преобразования, первая из которых называется трансформацией, а вторая шифрованием.

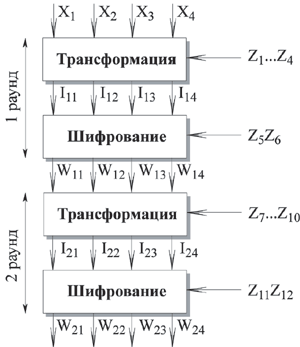
Рис. 3.5. Шифрование IDEA

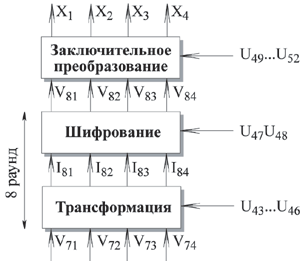
Рис. 3.6. Дешифрование IDEA

Рассмотрим преобразования, выполняемые в прямоугольниках на обоих рисунках. При шифровании поддерживаются следующие соотношения на выходе трансформации:

Y₁ = W₈₁ • Z₄₉ Y₃ = W₈₂ + Z₅₁Y₂ = W₈₃ + Z₅₀ Y₄ = W₈₄ • Z₅₂

Первая стадия первого раунда процесса дешифрования поддерживает следующие соотношения:

J₁₁ = Y₁ • U₁ J₁₃ = Y₃ + U₃J₁₂ = Y₂ + U₂ J₁₄ = Y₄ • U₄

Подставляя соответствующие значения, получаем:

J₁₁ = Y₁ • Z₄₉^-1 = W₈₁ • Z₄₉ • Z₄₉^-1 = W₈₁J₁₂ = Y₂ + -Z₅₀ = W₈₃ + Z₅₀ = W₈₃ + Z₅₀ + -Z₅₀ = W₈₃J₁₃ = Y₃ + -Z₅₁ = W₈₂ + Z₅₁ + -Z₅₁ = W₈₂J₁₄ = Y₄ • Z₅₂^-1 = W₈₄ • Z₅₂ • Z₅₂^-1 = W₈₄

Таким образом, выход первой стадии процесса дешифрования эквивалентен входу последней стадии процесса шифрования за исключением чередования второго и третьего блоков. Теперь рассмотрим следующие отношения:

W₈₁ = I₈₁ MA_R(I₈₁ I₈₃, I₈₂ I₈₄)W₈₂ = I₈₃ MA_R(I₈₁ I₈₃, I₈₂ I₈₄)W₈₃ = I₈₂ MA_L(I₈₁ I₈₃, I₈₂ I₈₄)W₈₄ = I₈₄ MA_L(I₈₁ I₈₃, I₈₂ I₈₄)

Где MA_R(X, Y) есть правый выход МА структуры с входами Х и Y, и MA_L(X, Y) есть левый выход МА структуры с входами Х и Y. Теперь получаем

V₁₁ = J₁₁ MA_R (J₁₁ J₁₃, J₁₂ J₁₄) = W₈₁ MA_R(W₈₁ W₈₂, W₈₃ W₈₄) = I₈₁ MA_R(I₈₁ I₈₃, I₈₂ I₈₄) MA_R[ I₈₁ MA_R(I₈₁ I₈₃, I₈₂ I₈₄) I₈₃ MA_R(I₈₁ I₈₃, I₈₂ I₈₄), I₈₂ MA_L(I₈₁ I₈₃, I₈₂ I₈₄) I₈₄ MA_L(I₈₁ I₈₃, I₈₂ I₈₄) ] = I₈₁ MA_R(I₈₁ I₈₃, I₈₂ I₈₄) MA_R(I₈₁ I₈₃, I₈₂ I₈₄) = I₈₁

Аналогично мы имеем

V₁₂ = I₈₃V₁₃ = I₈₂V₁₄ = I₈₄

Таким образом, выход второй стадии процесса дешифрования эквивалентен входу предпоследней стадии процесса шифрования за исключением чередования второго и третьего подблоков. Аналогично можно показать, что

V₈₁ = I₁₁V₈₂ = I₁₃V₈₃ = I₁₂V₈₄ = I₁₄

Наконец, так как выход трансформации процесса дешифрования эквивалентен первой стадии процесса шифрования за исключением чередования второго и третьего подблоков, получается, что выход всего процесса шифрования эквивалентен входу процесса шифрования.

Дата добавления: 2014-12-23