Владимир – 2009

Расчётно-графическая работа

По дисциплине
«Устойчивость систем электроснабжения»

Выполнил:
Ст. гр. ЗЭС93–108
Файхутдинов М.Ю.

Проверил:
доцент, к.т.н.
Шмелёв В.Е.

Вариант Z.

Задание.

Дана электронная схема, изображённая на рис. 1 и состоящая из двух операционных усилителей и однофазного трансформатора. Трансформатор представлен в виде схемы замещения, учитывающей основные и паразитные параметры.

Определить устойчивость электронной схемы тремя способами:

1. Путём непосредственного определения полюсов передаточной функции замкнутой системы;

2. По критерию Рауса;

3. По критерию Найквиста.

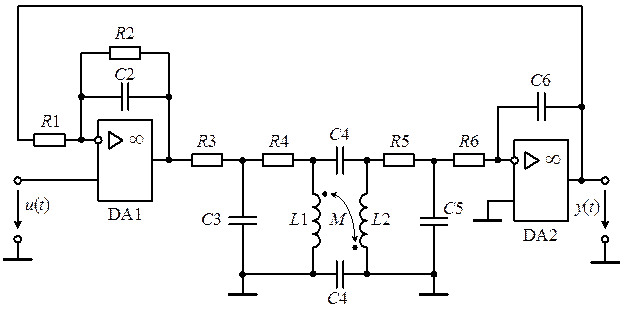
Рис. 1. Функциональная схема электронной динамической системы

Параметры схемы для данного варианта имеют следующие значения:

R ₁ = 22 кОм;

R ₂ = 10 кОм;

R ₃ = 10 Ом;

R ₄ = 20 Ом;

R ₆ = 2 кОм;

C ₂ = 1 нФ;

C ₃ = 400 пФ;

C ₄ = 50 пФ;

C ₆ = 20 нФ;

Коэффициент электромагнитной связи обмоток трансформатора k _эм = 0.99;

Индуктивность первичной обмотки L ₁ = 1 Гн = 1000 мГн; коэффициент трансформации k _T = 2.5.

В расчётах для удобства сопротивления будем записывать в килоомах, индуктивности – в миллигенри, ёмкости – в нанофарадах, тогда время будет измеряться в микросекундах, частота – в мегагерцах, циклическая частота – в рад/мкс, комплексная частота – в мкс^-1.

Рассчитаем индуктивность вторичной обмотки: L ₂ = L ₁/ k _T² = 160 мГн.

Рассчитаем взаимную индуктивность обмоток трансформатора:

= 0.396 Гн = 396 мГн.

В соответствии с заданием способ намотки обмоток трансформатора таков, что ёмкость вторичной обмотки связана с ёмкостью первичной обмотки соотношением C ₅ = C ₃/ k _T². Рассчитываем C ₅ = 64 пФ = 0.064 нФ.

Способ намотки обмоток трансформатора таков, что сопротивление вторичной обмотки связано с сопротивлением первичной обмотки соотношением R ₅ = R ₄/ k _T. Рассчитываем R ₅ = 8 Ом = 0.008 кОм.

Функциональной электрической схеме, изображённой на рис. 1, соответствует структурная схема динамической системы, изображённая на рис. 2. Здесь обозначено: H ₁(s) – передаточная функция усилительного каскада (DA1, R 1, R 2, C 2) по неинвертирующему входу; H ₂(s) – передаточная функция того же каскада по инвертирующему входу, она выполняет роль передаточной функции отрицательной обратной связи; H ₃(s) – передаточная функция трансформатора; H ₄(s) – передаточная функция усилительного каскада (DA2, R 6, C 6).

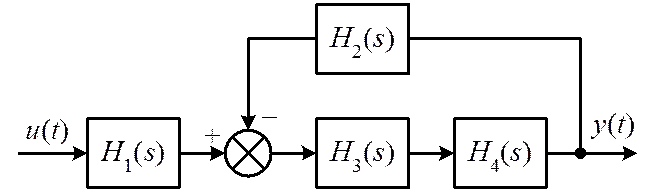
Рис. 2. Структурная схема анализируемой динамической системы

Для анализа устойчивости работы динамической системы нужно определить все названные передаточные функции.

;

;

.

Чтобы рассчитать передаточную функцию H ₃(s), нужно выполнить анализ схемы замещения трансформатора операторным методом. Воспользуемся системой MATLAB и вычислительным сценарием cepye, подключив к нему Symbolic Mach Toolbox. В командном окне MATLAB выполним следующую последовательность операторов:

s=tf([1 0],1);

TM=[1 1 0 0 0 0 0 0; 0 -1 1 1 0 0 0 0; 0 0 0 -1 1 1 0 0; 0 0 0 0 0 -1 1 1];

pv=[tf(0.01) (tf(0.4)*s)^-1 tf(0.02) tf(1000)*s (tf(0.05)*s)^-1 tf(160)*s tf(0.008) (tf(0.5)+tf(0.064)*s)^-1];

PV(4,6)=-tf(396)*s;

PV(6,4)=-tf(396)*s;

PM=TM*PV*TM.'; % Матрица контурных сопротивлений

PS=TM.'/PM*TM; % Матрица входных и взаимных проводимостей ветвей

KS=-PS*PV; % Матрица коэффициентов передачи тока

KC=PV*PS-eye(size(PV)); % Матрица коэффициентов передачи напрqжения.

PC=PV*KS+PV; % Матрица входных и взаимных сопротивлений ветвей

H3=minreal(KC(8,1));

H3=minreal_sh(H3)

Переменная TM соответствует матрице главных контуров схемы замещения трансформатора, равной

После выполнения записанной последовательности операторов в командном окне появится выражение для передаточной функции трансформатора:

Transfer function:

1.562e004 s^3 + 1.388e-008 s^2 - 146.8 s + 1.134e-009

---------------------------------------------------------

s^5 + 876.3 s^4 + 1.416e005 s^3 + 1.563e005 s^2 + 379.9 s

Переменная H3 будет содержать tf- выражение искомой передаточной функции H ₃(s). Введём в ЭВМ передаточные функции усилительных каскадов:

H1=(tf(6)+tf(10)*s)/(tf(1)+tf(10)*s);

H2=tf(5)/(tf(1)+tf(10)*s);

H4=-tf(1)/s/tf(40);

Посчитаем передаточную функцию замкнутой системы без учёта H ₁(s):

W=minreal(H3*H4/(1+H2*H3*H4));

W=minreal_sh(W,0.4)

Transfer function:

-390.6 s^4 - 8.292e004 s^3 - 8285 s^2 + 778.9 s + 77.85

-------------------------------------------------------------------------------

s^7 + 1089 s^6 + 3.277e005 s^5 + 3.024e007 s^4 + 3.618e007 s^3 + 3.355e006 s^2

+ 8062 s + 389.3

Определим корни знаменателя этой передаточной функции:

[b,a]=tfdata(W,'v');

ss=roots(a)

ss =

-662.96

-212.18

-212.18

-1.1098

-0.099916

-0.00057583 + 0.01083i

-0.00057583 - 0.01083i

Расчёт импульсной характеристики показал, что передаточная функция W (s) имеет семь полюсов. Все они имеют отрицательную действительную часть, следовательно, анализируемая динамическая система устойчива. Передаточная функция H ₁(s) не охвачена обратной связью и не содержит правых и мнимых полюсов, значит, она не влияет на устойчивость динамической системы. Поэтому при анализе устойчивости передаточная функция H ₁(s) не учитывалась.

Для подтверждения сказанного покажем последовательность операторов и сообщений в командном окне MATLAB при построении графика импульсной характеристики замкнутой системы с учётом передаточной функции H ₁(s).

W1=minreal(H1*W);

W1=minreal_sh(W1)

impulse(W1,5/min(abs(real(ss))))

grid on

set(findobj('type','line'),'linewidth',2,'color',[0 0 0])

Передаточная функция замкнутой системы W1 имеет вид

Transfer function:

-390.6 s^4 - 8.312e004 s^3 - 4.973e004 s^2 + 780.7 s + 467.1

-------------------------------------------------------------------------------

s^7 + 1089 s^6 + 3.277e005 s^5 + 3.024e007 s^4 + 3.618e007 s^3 + 3.355e006 s^2

+ 8062 s + 389.3

График импульсной характеристики замкнутой системы показан на рис. 3. Видно, что устойчивость проявляется в виде затухания колебаний.

Рис. 3. Импульсная характеристика замкнутой системы

Проведём анализ устойчивости вторым способом. Составим таблицу (матрицу) Рауса для передаточной функции W ₁(s). Для этого сначала в массив-строку с именем a запишем коэффициенты полинома знаменателя передаточной функции W1:

[b,a]=tfdata(W1,'v')

b =

Columns 1 through 6

0 0 0 -390.62 -83119 -49727

Columns 7 through 8

780.73 467.12

a =

Columns 1 through 6

1 1088.5 3.2768e+005 3.0243e+007 3.6177e+007 3.3548e+006

Columns 7 through 8

8062.5 389.26

r=raus(a)

r =

1 3.2768e+005 3.6177e+007 8062.5

1088.5 3.0243e+007 3.3548e+006 389.26

2.9989e+005 3.6174e+007 8062.1 0

3.0112e+007 3.3548e+006 389.26 0

3.6141e+007 8058.2 0 0

3.3481e+006 389.26 0 0

3856.3 0 0 0

389.26 0 0 0

Видно, что в первом столбце этой матрицы нет перемен знака чисел. Из этого следует, что число правых полюсов передаточной функции W ₁(s) равно нулю. Это означает, что анализируемая система устойчива. В предыдущем способе анализа также не было найдено ни одного правого комплексного полюса.

Использованная в данной последовательности операторов m-функция raus содержит следующие операторы MATLAB:

% raus - Составление матрицы Рауса для полинома

% r=raus(p)

% p - массив-строка коэффициентов полинома, для которого

% составляется матрица Рауса

% r - матрица Рауса

function r=raus(p)

n1=length(p); % длина массива коэффициентов полинома

n2=ceil(n1/2); % число столюцов матрицы Рауса

r=zeros(n1,n2); % распределяем память под матрицу Рауса

if p(1)==0, return, end

if mod(n1,2)==0 % если длина полинома чётная

r([1,2],:)=reshape(p,2,n2);

else

r([1,2],:)=reshape([p,0],2,n2);

end % if mod(n1,2)==0

% Цикл вычислений. Анализируется особые случаи

for k=3:n1

if ~any(r(k-1,:)), r(k-1,:)=r(k-2,:).*(n1-k+2-(0:n2-1)*2); end

if r(k-1,1)==0, r(k-1,1)=eps(max(abs(r(k-1,:))))*sign(r(k-2,1)); end

r(k,1:end-1)=-r(k-2,1)/r(k-1,1)*r(k-1,2:end)+r(k-2,2:end);

end

Проведём анализ устойчивости третьим способом. Рассчитаем передаточную функцию разомкнутой системы, равную произведению передаточных функций элементов контура структурной схемы с отрицательной обратной связью.

H _p(s) = H ₂(s)× H ₃(s)× H ₄(s) =

= -7.812e004 s^3 - 6.941e-008 s^2 + 733.8 s - 5.672e-009

-------------------------------------------------------------------------------

400 s^7 + 3.505e005 s^6 + 5.669e007 s^5 + 6.817e007 s^4 + 6.402e006 s^3

+ 1.52e004 s^2.

В командном окне MATLAB выполним последовательность операторов

om=logspace(-3,1,1001);

Hr=H2*H3*H4;

[b,a]=tfdata(Hr,'v');

Hrom=polyval(b,1i*om)./polyval(a,1i*om);

Lr=20*log10(abs(Hrom));

Pr=angle(-Hrom)-pi;

subplot(2,1,1)

semilogx(om,Lr,'k-','linewidth',2)

grid on

subplot(2,1,2)

semilogx(om,Pr*180/pi,'k-','linewidth',2)

grid on

В результате в одной фигуре MATLAB будет построено два графика: ЛАЧХ и ЛФЧХ разомкнутой системы (рис. 4). По графику или с помощью интерполяции ЛФЧХ определим частоту (рад/мкс), на которой ЛФЧХ проходит через -180^О:

om1=interp1(Pr,om,-pi,'cubic')

om1 =

0.01493

По графику или с помощью интерполяции определим частоту (рад/мкс), на которой модуль коэффициента передачи сигнала равен 0 дБ:

om2=interp1(Lr,om,0,'cubic')

om2 =

0.010747

Модуль коэффициента передачи сигнала (дБ) на частоте om1 определяется оператором:

D1=interp1(om,Lr,om1,'cubic')

D1 =

-5.5566

Это означает, что система устойчива. Запас устойчивости по модулю составляет 5.5566 дБ.

Дефицит устойчивости по фазе (в градусах) определяется по значению ЛФЧХ на частоте om2 оператором:

D2=(-pi-interp1(om,Pr,om2,'cubic'))*180/pi

D2 =

-6.081

Запас устойчивости по модулю составляет 6.081 градусов.

Вывод. Анализ устойчивости динамической системы тремя методами дал один и тот же результат: система устойчива. Первый из этих трёх методов наиболее универсален, но обязательно требует применения вычислительной техники и современного математического ПО. Второй из этих методов не требует применения вычислительной техники и позволяет определить число правых полюсов передаточной функции замкнутой системы. Однако этот метод не позволяет анализировать динамические системы с элементами чистого запаздывания. Этого недостатка лишён третий метод анализа, который также не требует применения вычислительной техники и, кроме всего прочего, позволяет определить запас или дефицит устойчивости по модулю и по фазе, что бывает важно при выборе и синтезе корректирующих устройств.

Рис. 4. ЛАЧХ (сверху) и ЛФЧХ (снизу) разомкнутой системы

Дата добавления: 2015-01-03