
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение
|
|
|
|
1) По условию 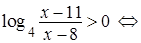
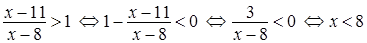 .
.
Если 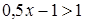 ,
, 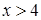 , то
, то 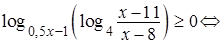
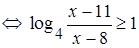
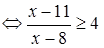
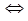
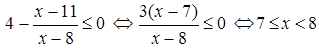 .
.
Если 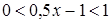 ,
, 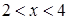 , то
, то 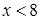 и
и 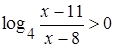 . Кроме того, так как
. Кроме того, так как 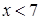 , то
, то 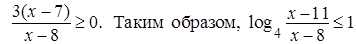 . Значит,
. Значит, 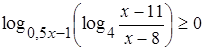 . Следовательно, все числа в интервале
. Следовательно, все числа в интервале 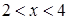 являются решениями исходного неравенства.
являются решениями исходного неравенства. 
Объединяя найденные множества решений, получаем ответ: 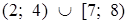 .
.
2) Пусть 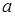 и
и 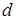 – первый член и разность прогрессии. Если
– первый член и разность прогрессии. Если 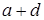 и
и 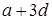 лежат в одном и том же из двух промежутков
лежат в одном и том же из двух промежутков 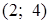 и
и 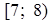 , то в нем лежит и
, то в нем лежит и 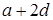 . Но тогда третий член прогрессии также будет решением заданного неравенства. Противоречие. Значит,
. Но тогда третий член прогрессии также будет решением заданного неравенства. Противоречие. Значит,
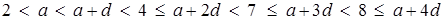 .
.
3) Требуется найти все значения 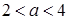 , при которых эта система неравенств имеет решения относительно
, при которых эта система неравенств имеет решения относительно 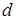 . Выпишем четыре неравенства относительно
. Выпишем четыре неравенства относительно 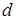 :
:
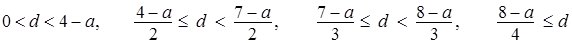 .
.
 Систему этих линейных неравенств решим графическим способом. Построим прямые
Систему этих линейных неравенств решим графическим способом. Построим прямые 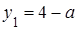 ,
, 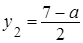 ,
, 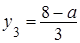 ,
, 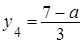 ,
, 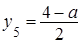 ,
, 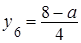 .
.
На интервале 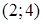 прямая
прямая 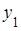 лежит ниже прямых
лежит ниже прямых 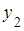 и
и 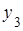 , а прямая
, а прямая 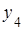 лежит выше прямых
лежит выше прямых 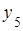 и
и 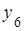 ,
,
4) Поэтому достаточно найти все значения 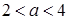 , при которых решения имеет только одно неравенство
, при которых решения имеет только одно неравенство 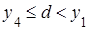 . Прямые
. Прямые 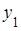 и
и 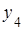 пересекаются в точке
пересекаются в точке 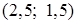 и
и 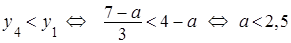 .
.
Ответ: 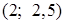 .
.
| Баллы | Критерии оценки выполнения задания С5 |
Приведена верная последовательность всех шагов решения:
1) нахождение множества решений логарифмического неравенства;
2) запись условия задачи в виде неравенств относительно 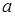 и и 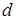 ;
3) рассмотрение системы четырех двойных неравенств относительно ;
3) рассмотрение системы четырех двойных неравенств относительно 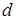 ;
4) сведение к случаю одного двойного неравенства, его решение.
Обоснованы все моменты решения:
а) в шаге 1) преобразования обоснованы или ссылками на свойства логарифмов, или явными указаниями на равносильность этих преобразований;
б) в шаге 2) принадлежность ;
4) сведение к случаю одного двойного неравенства, его решение.
Обоснованы все моменты решения:
а) в шаге 1) преобразования обоснованы или ссылками на свойства логарифмов, или явными указаниями на равносильность этих преобразований;
б) в шаге 2) принадлежность 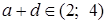 и и 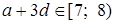 обоснована ссылкой на то, что обоснована ссылкой на то, что 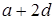 – не решение логарифмического уравнения;
в) шаг 3) обоснован или верным построением графиков прямых, или алгебраической проверкой расположения прямых на интервале – не решение логарифмического уравнения;
в) шаг 3) обоснован или верным построением графиков прямых, или алгебраической проверкой расположения прямых на интервале 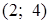 ;
г) в шаге 4) имеется ссылка на достаточность рассмотрения только одного двойного неравенства; явно приведено решение неравенства ;
г) в шаге 4) имеется ссылка на достаточность рассмотрения только одного двойного неравенства; явно приведено решение неравенства 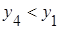 .
Все преобразования и вычисления верны. Получен верный ответ. .
Все преобразования и вычисления верны. Получен верный ответ.
| |
| Приведена верная последовательность всех шагов решения. В шаге 4) допустимо выписывание ответа со ссылкой только на графики. Обоснованы ключевые моменты а), б), в). Допустима 1 описка и/или негрубая вычислительная ошибка в шаге 4) в результате чего может быть получен неверный ответ. | |
Приведена в целом верная, но, возможно, неполная последовательность шагов решения. Верно выполнены шаги 1) и 2) решения, верно составлены все линейные неравенства относительно 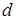 . Обоснованы ключевые моменты а) и б).
Допустимо, что дальнейшее выполнение не завершено.
Допустимы 1 – 2 негрубые ошибки в вычислениях или построениях графиков, не влияющие на правильность дальнейшего хода решения. В результате может быть получен неверный ответ. . Обоснованы ключевые моменты а) и б).
Допустимо, что дальнейшее выполнение не завершено.
Допустимы 1 – 2 негрубые ошибки в вычислениях или построениях графиков, не влияющие на правильность дальнейшего хода решения. В результате может быть получен неверный ответ.
| |
| Общая идея, ход решения верны, но решение, возможно, не завершено. Верно выполнен шаг 1) решения. Обоснован ключевой момент а). Допустимо, что дальнейшее выполнение не завершено, а обоснования ключевых моментов б) – г) отсутствуют. Допустимы негрубые ошибки в вычислениях или преобразованиях. В результате этих ошибок может быть получен неверный ответ | |
| Все случаи решения, которые не соответствуют указанным выше критериям выставления оценок в 1, 2, 3, 4 балла. |
Примечание
Данное программное обеспечение можно скачать из интернета по указанным адресам.
| Сайт программы | http://www.dessci.com/en/ |
| Прямой линк (30 дней бесплатно) | http://www.dessci.com/en/dl/MathType52Setup.exe |
[1] Неточностью в обоснованиях является замена свойства на определение или на признак, или наоборот, а также неверные названия теорем или формул.
[2] Неточностью в обоснованиях является замена свойства на определение или на признак, или наоборот, а также неверные названия теорем или формул.
|
|
|
|
|
Дата добавления: 2015-01-03; Просмотров: 307; Нарушение авторских прав?; Мы поможем в написании вашей работы!