Кинетика окисления металлов на воздухе

ХИМИЧЕСКАЯ КОРРОЗИЯ МЕТАЛЛОВ.

Закон роста оксидной пленки во времени в значитель­ной степени зависит от ее защитных свойств.

У незащитных пленок, например несплошных (для которых отношение объем оксида к объему металла <1), скорость роста постоянная (не зависит от толщины об­разующейся пористой пленки) и контролируется химической реакцией образования пленки из металла и кис­лорода, являющейся наиболее заторможенной стадией процесса (кинетический контроль). В этом случае наблю­дается линейный закон роста пленки

^,

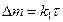где Δ m – удельное увеличение массы образца, г/м²; k₁ – постоянная, г/(м²·ч); τ – время окисления металла, ч.

У обладающих защитными свойствами сплошных пленок (для которых отношение объем оксида к объему металла >1) скорость роста часто контролируется диф­фузией реагентов, которая является наиболее затормо­женной стадией процесса (диффузионный контроль) и сопровождается самоторможением: по мере утолщения пленки уменьшается скорость диффузии через нее реагентов (металла и кислорода), а следовательно, и ско­рость коррозионного процесса. В этом случае пленка растет по параболическому закону

^,

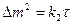где k₂ — постоянная, г²/ (м⁴·ч).

Если скорость роста пленки контролируется и ско­ростью химической реакции, и скоростью диффузии че­рез пленку реагентов (смешанный диффузионно-кинети­ческий контроль), то рост пленки может быть описан квадратным уравнением Эванса

^,

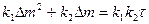где k₁ и k₂ — постоянные (см. выше),

или степенным законом

^,

где n — показатель степенного закона, причем 1< n <2; k_n — постоянная, гⁿ/(м²ⁿ·ч).

В ряде случаев окисления металлов наблюдается торможение процесса в большей степени, чем это сле­дует из первого закона диффузии (контроль переносом электронов через тонкие пленки путем туннельного эф­фекта или дополнительное препятствие диффузии обра­зующимися в пленке микропузырями). В этих случаях рост пленки происходит по степенному закону

^,

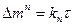где n — показатель степенного закона, причем n>2,. или по логарифмическому закону

^,

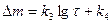где k₃ и k₄ — постоянные.

В реальных процессах окисления металлов часто наблюдаются нарушения приведенных выше зависимостей Δ m = f (τ) вследствие ряда факторов, осложняющих процесс (нарушение сплошности пленки внутрен­ними напряжениями, возникающими при росте защит­ной пленки или изменении температуры, и др.), а так­же более сложные зависимости, которые описывают процесс роста окисной пленки во времени.

На основании опытных данных об изменении массы образца по времени можно получить уравнение, которое дает возможность составить суждение о механизме и контролирующем факторе процесса и рассчитывать коррозионное разрушение металла при его окислении как функцию времени.

1.1 Графическое дифференцирование

Для графического определения производной функ­ции y = f (x) при определенном значении х ₁ (рис.1) сле­дует построить касатель­ную к кривой в точке (x ₁, y ₁) и определить тангенс угла α, образу­емого этой касательной с положительным нап­равлением оси Х. Это следует из того, что, как известно

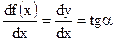
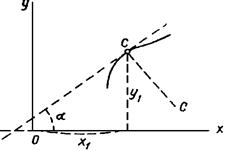Рисунок 1.1 - Графическое дифференцирование

Эта задача графически может быть решена только приближенно, так как провести касательную в данной точке произвольной кривой можно лишь с очень ограниченной точностью. При таких построениях рекомендует­ся проводить вспомогательную нормаль СС, считая не­большой участок кривой вблизи точки (x ₁, y ₁) дугой ко­нического сечения, в простейших случаях — окружно­сти. Построение нормали можно выполнить несколько точнее.

Дата добавления: 2014-12-23