Програма. Численное моделирование рассеяния поля плоской волны на идеально проводящем бесконечном цилиндре произвольного сечения методом интегральных уравнений первого

Численное моделирование рассеяния поля плоской волны на идеально проводящем бесконечном цилиндре произвольного сечения методом интегральных уравнений первого рода для потенциала простого слоя.

(курсовая работа)

Процесс рассеяния плоской электромагнитной волны на гладком металлическом теле вполне адекватно описывается диаграммой рассеянного поля, характеризующей распределение рассеянной энергии по угловым координатам.

Общая система стационарных уравнений Максвелла (при гармонической зависимости 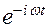всех векторных полей от времени) имеет вид

rot 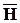+ iw e = ;

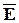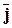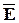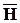rot - iwm = 0;

и в случае рассеяния Е - поляризованной плоской волны на бесконечном металлическом цилиндре с направляющей G, при ее распространении в ортогональном оси цилиндра направлении, сводится к скалярной плоской задаче для уравнения Гельмгольца в полярных координатах относительно z – компоненты u(М) = Е_z электрического поля с краевым условием первого рода на границе контура поперечного сечения цилиндра, то есть к задаче вида

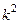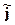D u + u = ; (1)

u|_G = 0;

где k = w 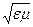-волновое число, если из второго уравнения системы Максвелла выразить 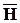, подставить в первое уравнение и воспользоваться известным тождеством rotrot 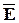= grad(div 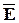) - D 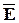, с учетом того, что поле имеет отличной от нуля лишь компоненту Е_z [1]. Краевая задача (1) может быть поставлена и как полостью однородная, то есть

D u + 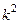u = 0; (1)’

u|_S = 0;

если в качестве возбуждающего поля взять плоскую волну 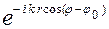, распространяющуюся из бесконечно удаленной точки к началу координат (так как временная зависимость полей от времени полагается имеющей вид 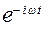). Несмотря на однородность задачи (1)’, она имеет нетривиальное решение, так как плоская волна не удовлетворяет условию излучения Зоммерфельда на бесконечности [2]. Выделяя в решении u(r,j) рассеянную волну: u(r,j) = u_s(r,j) + 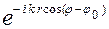, удовлетворяющую условию излучения, получим для u_s(r,j) краевую задачу вида

D u_s + 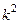u_s = 0; (2)

u_s|_G = - ;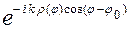

где G - контур поперечного сечения цилиндра, описываемый в полярных координатах уравнением r = r(j), j₀ - угол падения плоской волны.

Рассеянное поле u_s может быть представлено потенциалом простого слоя:

u_s(М) = 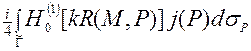, (3)

где 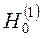- функция Ханкеля первого рода, нулевого порядка; 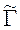- контур, расположенный внутри G, и подобный ему: r = ar(j), причем a £ 1. При этом, P – точки а контуре 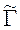, а

М – в пространстве, вне контура G; k – волновое число; R (M, P) – декартово расстояние между точками M и P: R (M, P) = {r ² + a ²r ² (y) - 2a rr (y)cos(j - y)}^1/2; j(P) - вспомогательный ток на контуре 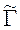, имеющий смысл обычного электрического тока на поверхности металла, если контура G и 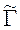совпадают (a = 1). Представление (3) удовлетворяет всем условиям задачи (2), кроме краевого. Используя это представление, краевое условие в задаче (2) можно записать в виде интегрального уравнения первого рода

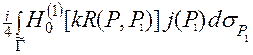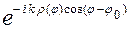= - , (4)

где искомой функцией является ток j(P).

Функция Ханкеля 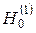= J₀ + iN₀, где функции Бесселя J₀ и Неймана N₀ вычисляются с помощью стандартных процедур из библиотек наиболее распространенных языков программирования.

Интегральное уравнение первого рода (4), с гладким ядром хотя и является формально некорректно поставленной задачей, приводит к устойчивым вычислительным процедурам при его замене на систему алгебраических уравнений, если контура G и 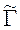достаточно близки, что обеспечивает в матрице алгебраической системы преобладание главой диагонали.

Более подробная запись интегрального уравнения (4):

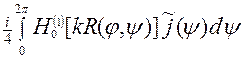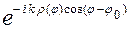= - , (5)

где R (j, y) = {r ²(j) + a ²r ²(y) - 2ar(j)r(y)cos(j - y)}^1/2; 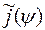dy = j(y)a 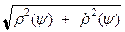dy - ток, умноженный на дифференциал дуги контура.

Если ток 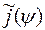найден из уравнения (5) (точно или приближенно), то потенциал простого слоя (3) явно описывает поведение рассеянного поля всюду вне контура G. Нас будет интересовать дальняя зона, то есть значения kR (M, P) = k{r ² + a ²r ² (y) - 2a rr (y)cos (j - y)}^1/2 при k r >> 1. При этом и kR (M, P) >> 1, что позволяет заменить функцию Ханкеля ее асимптотикой: 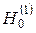(kR)» 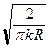exp[i(kR - p /4)] [3]. Приближая радикал в выражении

kr{1 + a ²r ² (y)/r ² - 2a r (y)cos (j - y)/r}^1/2 первыми двумя членами биномиального ряда, получим kR (M, P)» kr{1 + a ²r ² (y)/2r ² - a r (y)cos(j - y)/r}»

kr - ka r (y)cos (j - y) + O(1/r). При этом, 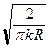» 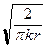. Следовательно, в дальней зоне рассеянное поле приближенно описывается выражением

u_s(М)» 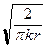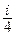exp[ikr - i p /4] 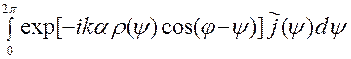. (6)

Множитель 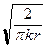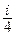exp[ikr - i p /4] перед интегралом в (6), зависящий только от радиуса r, и ответственный за порядок убывания амплитуды поля равномерно по r при удалении от рассеивающего тела, можно не рассматривать. Остающееся выражение

F(j) = 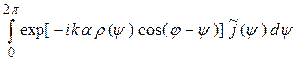(7)

называют обычно функцией ослабления [4]. Она характеризует распределение интенсивности рассеянного поля по угловой координате j для каждого значения полярного радиуса r. Модуль | F(j)| этой функции носит название диаграммы рассеяния (или диаграммы направленности) и ее приближенное вычисление является основной целью данной работы.

Интегральное уравнение первого рода (5) заменяем приближенно алгебраической системой линейных уравнений, вводя равномерные сетки: y_m = 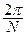(m + 1/2); m = 0, … N - 1; j_n = 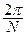(n + 1/2); n = 0, …N – 1.

В результате, получим алгебраическую систему вида

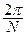
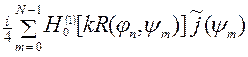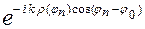= - . (8)

Находя с помощью численного метода приближенное решение { 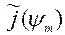} системы (8), получим выражение для диаграммы рассеяния в виде одномерного массива вида

F(j_n) = 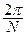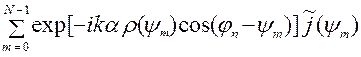, (9)

что позволяет строить графики для | F(j _n)| при различных значениях параметров N, a, j₀.

Расчеты необходимо провести при нескольких значениях N, проверяя сходимость приближенного метода, а также при нескольких значениях a, близких к единице, и играющего роль параметра регуляризации, а также при нескольких значениях угла падения j₀, таких как 0, p /4; p /2; 3p /4; p; 3p /2.

Рассмотрим теперь вопрос о корректности задачи, сведенной к интегральному уравнению первого рода (4). Для этого заменим параметр a на 1 – p, (p ³ 0). При этом контуру G соответствует значение p = 0. Возьмем интегральное уравнение (5) для любого отличного от нуля значения p:

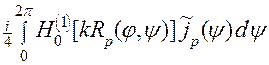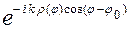= - , (10)

и представим ядро 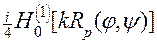интегрального оператора в виде первых двух слагаемых его разложении в ряд Маклорена по переменной p, в окрестности точки p = 0:

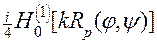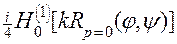= + p +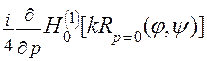

p ² 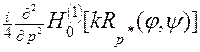, (11)

где p *Î[0, 1[ - значение переменной p, отличное от нуля. Из трех слагаемых формулы (11) лишь первые два имеют особенность при совпадении значений углов j и y. Первое из них имеет логарифмическую особенность и соответствует ядру обычного потенциала простого слоя. Второе имеет более сильную особенность, аналогичную ядру потенциала двойного слоя. Третье слагаемое, ввиду p* ¹ 0, является гладким аналитическим ядром без особенностей.

В соответствии с этим, представим левую часть уравнения (10) в виде

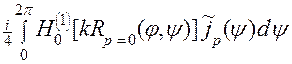+ p +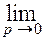

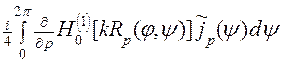+ p ² 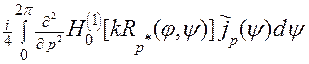. (12)

Ядро второго слагаемого в более подробной записи имеет вид

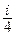k 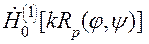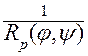[(p – 1) r ² (y) + r (j)r (y)cos(j - y)], и при

p® 0 переходит в

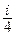k 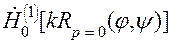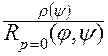[r (j)cos(j - y)] – r (y) ], (13)

cовпадая, с точностью до множителя – 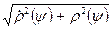с

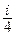
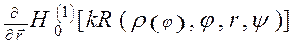_{| r ® r (y)}. Здесь 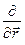- производная по направлению радиус-вектора. То есть,

=

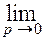
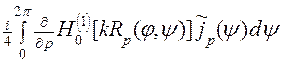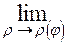
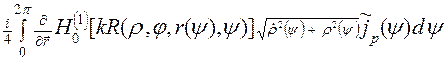– . (14)

Интеграл в (14) является обобщенным потенциалом двойного слоя, у которого ядро продифференцировано по направлению отличному от направления нормали. Из результатов приведенных в [5], следует общая формула для предельного значения такого потенциала, когда точка наблюдения стремится к поверхности:

=

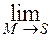
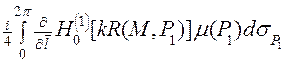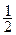
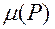cos( l, n ) + 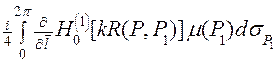. Следовательно, интегральные операторы в (12) приобретают окончательный вид

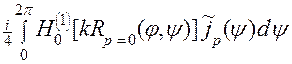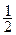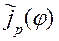– p cos( r, n ) –

p +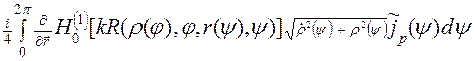

+ p ² .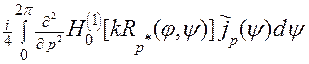

Из них, первый и второй имеют слабо полярные ядра, и являются, следовательно, вполне непрерывными, а последний – интегральный оператор с гладким ядром без особенностей. В результате, получаем интегральное уравнение Фредгольма второго рода относительно :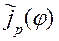

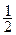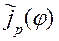p cos( r, n ) = –

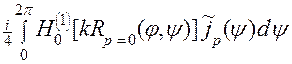p +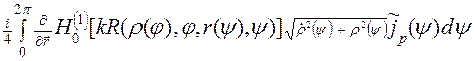

+ p ² 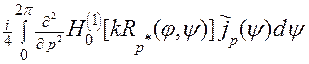+ 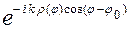, (15)

которое при p > 0 является корректно поставленной задачей.

Л И Т Е Р А Т У Р А

1. Л. А. Вайнштейн «Электромагнитные волны» М.: «Радио и связь» 1988

2. Зоммерфельд А. «Дифференциальные уравнения в частных производных физики». М.: И.Л., 1950

3. А.Н. Тихонов, А.А. Самарский «Уравнения математической физики».

М.: «Наука», 1966

4. Г.Т. Марков, Б.М. Петров, Г.П. Грудинская «Электродинамика и распространение радиоволн» М.: «Сов. Радио» 1979

5. Миранда К. Уравнения с частными производными эллиптического типа. М.: И.Л., 1957

інформаційно-навчального тренінгу

«Демократія та Мас-медіа»

Дата добавления: 2015-01-03