Оформите библиографическое описание источников 61 страница

SMF управления конфигурациями

· Предоставляет управляемую базу данных (CMDB) для журналов изменений, RFC, библиотеку эталонного ПО (Definitive Software Library — DSL), хранилище аппаратного обеспечения (Definitive Hardware Store — DHS), релизов и всех конфигурационных единиц.

· Требует привлечения SMF управления изменениями для обеспечения того, чтобы осуществлялось развертывание только утвержденных изменений и все операции отслеживания процесса утверждения проводились до конца.

· Требует привлечения SMF управления релизами для обновления CMDB и ввода в эту базу данных пакета релиза после развертывания.

SMF управления релизами

· Предоставляет оформленный в виде пакета релиз для всех изменений, развернутых на производстве. Требует привлечения SMF управления изменениями для утверждения изменений и их отслеживания на всем протяжении процесса релиза.

· Требует привлечения SMF управления конфигурациями для оценки влияния изменений на конфигурационные единицы и предоставления окончательно принятого хранилища для пакета релиза.

С управлением изменениями связаны также все прочие функции управления сервисом, поскольку каждая SMF испытывает непосредственное влияние того, какой способ управления изменениями применяется в каждой конкретной области. Это касается не только каждой из технологических областей, рассматриваемых в рамках квадранта эксплуатации, но и тех изменений, которые могут затрагивать процессы SMF в квадрантах поддержки и оптимизации.

Приложение. Рекомендуемые технологии

Все организации, намеревающиеся руководствоваться SMF управления изменениями для эффективного управления изменениями в своей производственной среде, могут использовать определенные инструментальные средства и технологии, позволяющие упростить данный процесс. Количество и сложность этих инструментальных средств зависят от размера организации и типа изменений, которые должны быть выполнены.

Как описано ниже, в процессе управления изменениями можно применить целый ряд инструментальных средств Microsoft.

· Запросы на изменения могут быть передаваться менеджеру изменений с помощью программ передачи сообщений по электронной почте, таких как Microsoft Outlook или Microsoft Exchange. Шаблоны для RFC могут создаваться как документы Word или Web-формы.

· Для управления изменениями в каждой фазе процесса может также использоваться календарная функция Microsoft Outlook, а для временных отсчетов, за которыми необходимо следить в процессах утверждении, разработки, развертывания и оценки изменения, могут устанавливаться предупреждающие сигналы. Календарная функция может также использоваться для публикации намеченного графика изменения.

· Владелец изменения при определении области действия изменения и затронутых сервисов может использовать инструментальное средство формирования рисунков и диаграмм Microsoft Visio® 2002 Enterprise Edition, а также систему Microsoft Systems Management Server (SMS).

· SMS может также использоваться как механизм распространения программного обеспечения, который позволит менеджеру изменений составлять отчеты о хода работ по реализации изменения вслед за его релизом и может оказаться полезным в процессе оценки результатов изменения.

· Microsoft Project представляет собой инструментальное средство, которое предоставляет менеджеру изменений возможность управлять и простыми, и сложными изменениями.

· Программы Exchange и NetMeeting позволяют проводить дистанционные совещания CAB, на которых должен быть утвержден или отклонен RFC.

(курсовая работа)

Процесс рассеяния плоской электромагнитной волны на гладком металлическом теле вполне адекватно описывается диаграммой рассеянного поля, характеризующей распределение рассеянной энергии по угловым координатам.

Общая система стационарных уравнений Максвелла (при гармонической зависимости 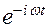всех векторных полей от времени) имеет вид

rot 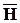+ iw e = ;

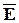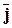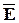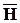rot - iwm = 0;

и в случае рассеяния Е - поляризованной плоской волны на бесконечном металлическом цилиндре с направляющей G, при ее распространении в ортогональном оси цилиндра направлении, сводится к скалярной плоской задаче для уравнения Гельмгольца в полярных координатах относительно z – компоненты u(М) = Е_z электрического поля с краевым условием первого рода на границе контура поперечного сечения цилиндра, то есть к задаче вида

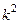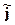D u + u = ; (1)

u|_G = 0;

где k = w 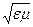-волновое число, если из второго уравнения системы Максвелла выразить 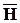, подставить в первое уравнение и воспользоваться известным тождеством rotrot 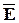= grad(div 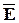) - D 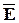, с учетом того, что поле имеет отличной от нуля лишь компоненту Е_z [1]. Краевая задача (1) может быть поставлена и как полостью однородная, то есть

D u + 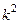u = 0; (1)’

u|_S = 0;

если в качестве возбуждающего поля взять плоскую волну 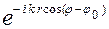, распространяющуюся из бесконечно удаленной точки к началу координат (так как временная зависимость полей от времени полагается имеющей вид 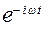). Несмотря на однородность задачи (1)’, она имеет нетривиальное решение, так как плоская волна не удовлетворяет условию излучения Зоммерфельда на бесконечности [2]. Выделяя в решении u(r,j) рассеянную волну: u(r,j) = u_s(r,j) + 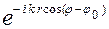, удовлетворяющую условию излучения, получим для u_s(r,j) краевую задачу вида

D u_s + 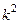u_s = 0; (2)

u_s|_G = - ;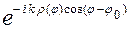

где G - контур поперечного сечения цилиндра, описываемый в полярных координатах уравнением r = r(j), j₀ - угол падения плоской волны.

Рассеянное поле u_s может быть представлено потенциалом простого слоя:

u_s(М) = 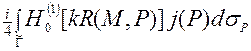, (3)

где 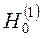- функция Ханкеля первого рода, нулевого порядка; 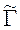- контур, расположенный внутри G, и подобный ему: r = ar(j), причем a £ 1. При этом, P – точки а контуре 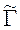, а

М – в пространстве, вне контура G; k – волновое число; R (M, P) – декартово расстояние между точками M и P: R (M, P) = {r ² + a ²r ² (y) - 2a rr (y)cos(j - y)}^1/2; j(P) - вспомогательный ток на контуре 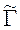, имеющий смысл обычного электрического тока на поверхности металла, если контура G и 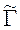совпадают (a = 1). Представление (3) удовлетворяет всем условиям задачи (2), кроме краевого. Используя это представление, краевое условие в задаче (2) можно записать в виде интегрального уравнения первого рода

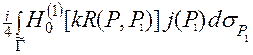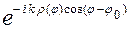= - , (4)

где искомой функцией является ток j(P).

Функция Ханкеля 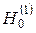= J₀ + iN₀, где функции Бесселя J₀ и Неймана N₀ вычисляются с помощью стандартных процедур из библиотек наиболее распространенных языков программирования.

Интегральное уравнение первого рода (4), с гладким ядром хотя и является формально некорректно поставленной задачей, приводит к устойчивым вычислительным процедурам при его замене на систему алгебраических уравнений, если контура G и 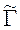достаточно близки, что обеспечивает в матрице алгебраической системы преобладание главой диагонали.

Более подробная запись интегрального уравнения (4):

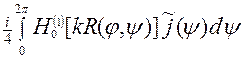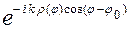= - , (5)

где R (j, y) = {r ²(j) + a ²r ²(y) - 2ar(j)r(y)cos(j - y)}^1/2; 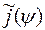dy = j(y)a 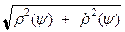dy - ток, умноженный на дифференциал дуги контура.

Если ток 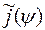найден из уравнения (5) (точно или приближенно), то потенциал простого слоя (3) явно описывает поведение рассеянного поля всюду вне контура G. Нас будет интересовать дальняя зона, то есть значения kR (M, P) = k{r ² + a ²r ² (y) - 2a rr (y)cos (j - y)}^1/2 при k r >> 1. При этом и kR (M, P) >> 1, что позволяет заменить функцию Ханкеля ее асимптотикой: 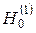(kR)» 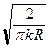exp[i(kR - p /4)] [3]. Приближая радикал в выражении

kr{1 + a ²r ² (y)/r ² - 2a r (y)cos (j - y)/r}^1/2 первыми двумя членами биномиального ряда, получим kR (M, P)» kr{1 + a ²r ² (y)/2r ² - a r (y)cos(j - y)/r}»

kr - ka r (y)cos (j - y) + O(1/r). При этом, 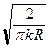» 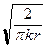. Следовательно, в дальней зоне рассеянное поле приближенно описывается выражением

u_s(М)» 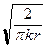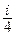exp[ikr - i p /4] 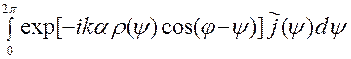. (6)

Множитель 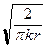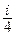exp[ikr - i p /4] перед интегралом в (6), зависящий только от радиуса r, и ответственный за порядок убывания амплитуды поля равномерно по r при удалении от рассеивающего тела, можно не рассматривать. Остающееся выражение

F(j) = 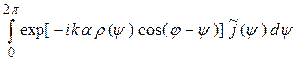(7)

называют обычно функцией ослабления [4]. Она характеризует распределение интенсивности рассеянного поля по угловой координате j для каждого значения полярного радиуса r. Модуль | F(j)| этой функции носит название диаграммы рассеяния (или диаграммы направленности) и ее приближенное вычисление является основной целью данной работы.

Интегральное уравнение первого рода (5) заменяем приближенно алгебраической системой линейных уравнений, вводя равномерные сетки: y_m = 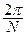(m + 1/2); m = 0, … N - 1; j_n = 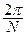(n + 1/2); n = 0, …N – 1.

Дата добавления: 2015-01-04