Постановка задачи. Пусть исходная таблица данных, содержащая значение аргумента и соответствующие им значения функции

Пусть исходная таблица данных, содержащая 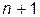значение аргумента 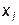и соответствующие им значения функции , получена в результате реализации некоторого численного алгоритма и размещена в текстовом файле фиксированного формата, например:

.

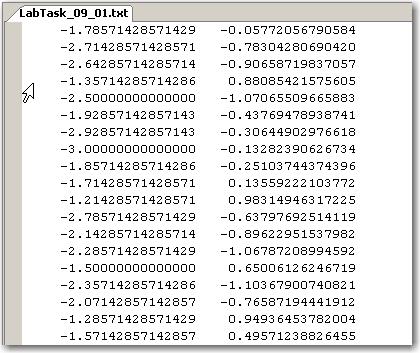(Фрагмент таблицы данных)

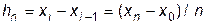Шаг изменения аргумента для данной таблицы является величиной постоянной.

Необходимо построить алгоритм и отладить программу, позволяющую в диалоговом режиме выполнения консольного приложения вычислять значения функции 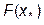для задаваемых пользователем значений аргумента .

В качестве интерполяционного многочлена необходимо использовать первую и вторую интерполяционные формулы Ньютона, построенные для конечных разностей 6-го порядка, т.е. :

, (9.1)

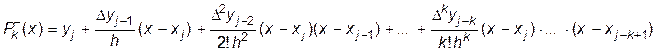. (9.2)

Выбор одной из двух представленных выше формул для конкретного вычисления должен базироваться на следующих рассуждениях. Заданное пользователем значение аргумента 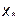обязательно должно удовлетворять условию 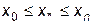. Следовательно, всегда найдется такая пара соседних узлов интерполирования, для которой будет иметь место двойное неравенство . Если при этом значение индекса 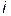окажется меньше чем , то будем применять первую интерполяционную формулу, т.е. (11.1). Если же , то применяем вторую формулу – (11.2), где . Такой подход обеспечит нам максимальную точность вычислений в рамках интерполирования по Ньютону с конечными разностями до 6-го порядка включительно, т.е. для .

Данный алгоритм не является единственно возможным, но для задач обучения вполне приемлем. Реализовав предложенную схему и убедившись в правильности вычислений, Вы можете в дальнейшем разработать свой алгоритм реализации интерполирования по Ньютону.

Поскольку исходные данные, размещенные в текстовом файле, не упорядочены по возрастанию аргумента (как того требует задача интерполирования), Вам предстоит в качестве первого пункта задания разработать алгоритм, состоящий из следующих этапов:

1. определения количества записей (пар чисел 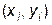) в файле данных:

2. выделения памяти под массивы аргумента и функции соответствующей размерности;

3. считывания данных из файла в подготовленные массивы;

4. сортировки массивов по возрастанию аргумента, т.е. 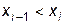для любого .

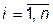Очевидно, что последний этап не должен изменять сами пары чисел .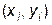

Исходные данные размещены в файлах LabTask_09_01.txt – LabTask_09_20.txt, где последние две цифры указывают на номер Вашего варианта.

Эти файлы генерируются уже известной Вам программой NMM_Labs и размещаются в директории (папке), откуда программа NMM_Labs загружается Вами на выполнение.

Для проверки корректности работы Вашего алгоритма Вы можете сгенерировать новую версию файла данных. При этом количество записей в файле будет уже другим (без изменения границ интерполирования и функционального представления интерполируемой функции).

Дата добавления: 2014-12-24