Типы зависимостей

Все зависимости между экономическими переменными можно разделить на 2 вида:

Функциональные. Если каждому значению независимой переменной или нескольким независимых переменных соответствует одно строго определенное значение зависимой переменной, то такая зависимость называется функциональной. В ней отсутствует воздействие случайных факторов, поэтому в экономике функциональная зависимость встречается редко.

Статистические. В экономике каждому значению независимых переменных может соответствовать несколько значений зависимой переменной в зависимости от воздействия неучтенных и случайных факторов. Например, пусть исследуется зависимость прибыли предприятия от объема производства и цены за единицу продукции. При одном и том же объеме производства и цене за единицу продукции прибыль предприятия может быть различна, т.к. на нее воздействуют множество других факторов, в том числе случайных.

Зависимость между переменными, на которую накладывается воздействие случайных факторов, называется статистической. Для нее характерно то, что изменение независимой переменной приводит к изменению математического ожидания зависимой переменной. Уравнение регрессии – математическая формула, описывающая статистическую зависимость между переменными. Если формула описывается линейной функцией, то регрессия называется линейной. Если нелинейной функцией – нелинейной регрессией. Если регрессия связывает одну зависимую и одну независимую переменную, то такая регрессия называется парной (простой). Если рассматривается зависимость экономической переменной от нескольких экономических переменных, то такая регрессия называется множественной.

Тема 2. Парная линейная регрессия

1. Истинное и выборочное уравнения регрессии.
Пусть исследуется статистическая зависимость экономического показателя У (объясняемая зависимая переменная) от экономического показателя Х (фактора, объясняющей или независимой переменной). Предположим, что зависимость носит линейный характер, тогда ее можно описать уравнением.

У= 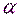+ 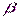Х+Е (1),
где Х – неслучайная величина, У и Е – случайные величины.

Случайная величина Е отражает воздействие на зависимую переменную У неучтенных и случайных факторов и называется ошибкой регрессии. Уравнение (1) называют истинным (теоретическим) уравнением регрессии или линейной регрессионной моделью. На основе реальных статистических данных об экономических показателях Х и У (выборке данных из генеральной совокупности) оцениваются параметры регрессии α и β и строится выборочное уравнение регрессии

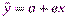, (2)

а, в, - коэффициенты регрессии. Уравнение (2) называют еще эмпирическим уравнением регрессии.

2. Суть метода наименьших квадратов.
Суть МНК состоит в минимизации суммы квадратов отклонений фактических значений результатного признака от его расчетных значений.

3. Геометрическая интерпретация метода наименьших квадратов.
начертим оси координат Х,У и изобразим в первой четверти точки (х_i,у_i)

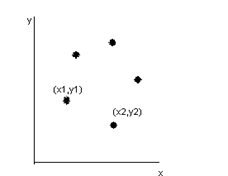
Полученное изображение называется диаграммой рассеяния или полем корреляции.

Проведем линию регрессии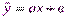

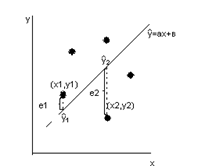
Согласно МНК, а и в должны быть такими, чтобы построенная линия была ближайшей к точкам поля корреляции по их совокупности.

Сумма квадратов расстояний от точек поля корреляции до линии регрессии должна быть минимальной.

4. Экономическая интерпретация коэффициентов парной линейной регрессии.
Коэффициент парной линейной регрессии в показывает, как в среднем изменяется зависимый экономический показатель у с изменением независимого фактора х на единицу. Коэффициент а парной линейной регрессии экономического смысла не имеет.

5. Основные предпосылки регрессионного анализа. Теорема Гаусса-Маркова.
Предпосылки:

1. Математическое ожидание случайного члена ε в любом наблюдении должно быть равно 0:

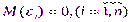
2. Дисперсия случайного члена ε должна быть постоянной для всех наблюдений:

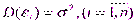
3. Случайные члены должны быть статистически независимы друг от друга:

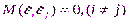
4. Объясняющая переменная х_i – неслучайная величина

Теорема Гаусса-Маркова:

Если выполняются предпосылки 1-4 регрессионного анализа, то оценки параметров теоретической регрессии а и в есть наилучшие линейные оценки, обладающие следующими свойствами:

1. Они являются несмещенными: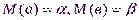

2. Они являются эффективными, т.е. имеют наименьшую дисперсию в классе всех несмещенных оценок.

(9)

3. Они являются состоятельными, т.е.

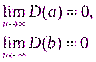
Это значит, что при достаточно большом объеме выборки n, оценки а и в близки к истинным параметрам линейной регрессионной модели α и β.

6. Расчет стандартных ошибок коэффициентов регрессии.
Стандартная ошибка регрессии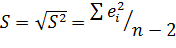
Стандартная ошибка коэфф. Регрессии: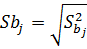

7.

Что такое статистическая значимость коэффициентов регрессии, как ее определить?
После построения уравнения регрессии необходимо сделать проверку его значимости: с помощью специальных критериев установить, не является ли полученная зависимость, выраженная уравнением регрессии, случайной, т.е. можно ли ее использовать в прогнозных целях и для факторного анализа. В статистике разработаны методики строгой проверки значимости коэффициентов регрессии с помощью дисперсионного анализа и расчета специальных критериев.
Статистическая значимость коэффициентов множественной линейной регресии с m обьясняющими переменными проверяется на основе t-статистики:
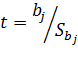
Наблюдаемое значение t-статістікі сравнивается с критической точкой распределения Стьюдента.Если |t|>этого коэффиц. Стьюдента,то коэфф. 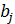считается статистически значимым,в обратном случае коэффициент считается статистически незначимым(близким к 0).

8. Оценка тесноты связи между переменными. Коэффициент корреляции.

Уравнение регрессии всегда дополняется показателем тесноты связи между переменными. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции: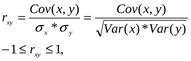

rxy – безразмерная величина, показывает степень линейной зависимости между переменными. Чем ближе rxy к ±1, тем сильнее линейная зависимость. Чем ближе rxy к 0, тем линейная зависимость слабее. Если rxy = ±1, то имеет место функциональная линейная зависимость. Если rxy = 0, то линейная зависимость отсутствует. Если rxy >0, то связь между переменными положительная, если rxy <0 – отрицательная.

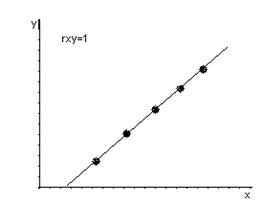
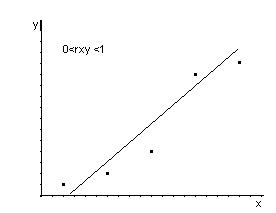
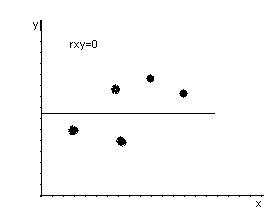
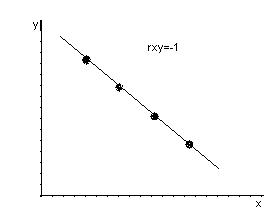
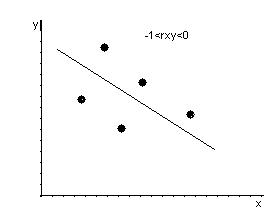
Рассчитаем коэффициент корреляции в примере 1: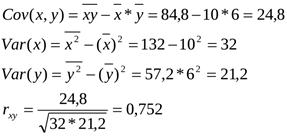

rxy >0 и близок к 1 следовательно линейная зависимость между прибылью предприятия и затратами на новое оборудование – положительная и тесная.

9. Проверка общего качества уровня регрессии. Коэффициент детерминации.
Общее качество уравнения регрессии оценивается по тому, как хорошо эмпирическое уравнение регрессии согласуется со статистическими данными. Другими словами, насколько широко рассеяны точки наблюдений относительно линии регресии.
Одной из наиболее эффективных оценок адекватности регрессионной модели, мерой качества уравнения регресии является коэффициент детерминации, определяемый по формуле: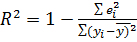
Чем теснее расположены точки относительно линии регресии,тем ближе коэффициент деерминации к 1.Чем слабее такая связь,тем коэфф. ближе к нулю.

10. Как оценить статистическую значимость коэффициента детерминации и уравнения в целом?

Т.к. R2 оценивается на основании выборочных данных, то его отличие от 0 может оказаться случайным. Поэтому проводят проверку его значимости:

1. Формулируется гипотеза Н0: R2=0, состоящая в том, что истинный коэффициент детерминации равен 0.

2. В качестве критерия проверки гипотезы применяют случайную величину F: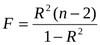

Величина F имеет распределение Фишера с двумя степенями свободы ν1=1, ν2=n-2.

Выберем уровень значимости проверки гипотезы значимости: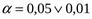

На основании α, ν1, ν2 в таблице распределения Фишера выбираем Fкр. (критическое)

Сравниваем Fрасч и Fкр.. если Fрасч > Fкр., то с вероятностью 1-α гипотезу Н0 считаем неверной, т.е. истинный коэффициент детерминации существенно отличен от нуля, уравнение регрессии значимо и переменные, включенные в уравнение регрессии достаточно объясняют поведение зависимой переменной. Если Fрасч < Fкр., то принимаемая гипотеза Н0, уравнение регрессии считается незначимым.

11. Виды прогноза

Под прогнозированием в эконометрике понимают построение оценки зависимой переменной для таких значений независимых переменных, которых нет в исходных наблюдениях.

Различают точечное прогнозирование и интервальное.

Точечный прогноз это число, значение зависимой переменной, вычисляемое для заданных значений независимых переменных.Интервальный прогноз это интервал, в котором с заданным уровнем значимости (с заданной вероятностью) находится истинное значение зависимой переменной для заданных значений независимых переменных.

3 тема.

1.Регрессии, нелинейные по переменным.

Нелинейность по переменным устраняется путем замены переменной.

Различают два класса нелинейной регрессии:

Класс I: Регрессия нелинейная, относительно включенных в анализ объясняющих переменных, но линейная по оцениваемым параметрам. Данный класс нелинейных регрессий включает уравне­ния, в которых зависимая переменная линейно связана с параметрами

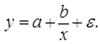Сюда входят: 1) равносторонние гиперболы

2) полиномы разных степеней

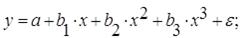
При оценке параметров регрессий нелинейных по объясняю­щим переменным используется подход, именуе­мый «замена переменных». Суть его состоит в замене «нели­нейных» объясняющих переменных новыми «линейными» переменными и сведение нелинейной регрессии к линейной регрессии. К новой «преобразованной» регрессии может быть приме­нен обычный метод наименьших квадратов (МНК).

2.Регрессии, нелинейные по параметрам.

Нелинейность по параметру часто устраняется путем логарифмического преобразования уравнения.

Класс II: Регрессия нелинейная по оцениваемым параметрам. К данному классу регрессий относятся уравнения, в которых зависимая переменная нелинейно связана с параметрами.

Сюда входят: А) степенная функция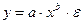

Б) показательная функция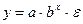

В) экспоненциальная функция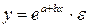

Г) другие функции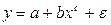

Если нелинейная модель внутренне линейна, то она с по­мощью соответствующих преобразований может быть при­ведена к линейному виду (например, логарифмированием и заменой переменных). Если же нелинейная модель внут­ренне нелинейна, то она не может быть сведена к линейной функции и для оценки её параметров используются итеративные процедуры, успешность которых зависит от вида уравнений и особен­ностей применяемого итеративного подхода.

3.Индекс корреляции и индекс детерминации.

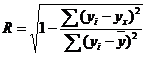Индекс корреляции.
Величина индекса корреляции R находится в границах от 0 до 1. Чем ближе она к единице, тем теснее связь рассматриваемых признаков, тем более надежно уравнение регрессии. Чем ближе значение индекса корреляции для нелинейных форм связи к единице, тем сильнее взаимосвязь между результативной и независимыми переменными, и наоборот, чем ближе значение индекса корреляции для нелинейных форм связи к нулю, тем слабее взаимосвязь между результативной и независимыми переменными.

Индекс детерминации.
Индексом детерминации называется квадрат индекса корреляции для нелинейных форм связи.

Индекс детерминации характеризует, на сколько процентов построенная модель регрессии объясняет вариацию значений результативной переменной относительно своего среднего уровня, т. е. показывает долю общей дисперсии результативной переменной, объяснённой вариацией факторных переменных, включённых в модель регрессии.
Чаще всего, давая интерпретацию индекса детерминации, его выражают в процентах.

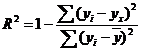
4.Эластичность функции.

Коэффициент эластичности показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%. Формула для расчета коэффициента эластичности имеет вид:

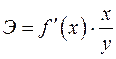
где 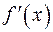- первая производная, характеризующая соотношение приростов результата и фактора для соответствующей формы связи.

Так как для остальных функций коэффициент эластичности не является постоянной величиной, а зависит от соответствующего значения фактора 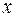, то обычно рассчитывается средний коэффициент эластичности.

Дата добавления: 2014-12-24