Постановка задачи. Пусть исследуемая функция либо имеет достаточно сложный функциональный вид, затрудняющий определение производной

Пусть исследуемая функция 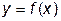либо имеет достаточно сложный функциональный вид, затрудняющий определение производной 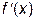, либо представляет собой некоторый численный алгоритм без функционального вида вообще.

Необходимо выяснить, имеет ли данная функция 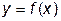на заданном интервале 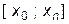точки экстремума 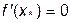, и если имеет – определить эти точки и значения функции 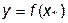в них.

Для выполнения данного задания заменить функцию 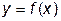системой квадратичных сплайнов, пользуясь методикой, изложенной выше.

Поиск экстремумов функции 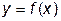необходимо производить по следующей схеме. Если на частичном отрезке интерполирования 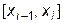квадратичный сплайн 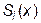имеет экстремум в точке 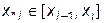, то и исследуемая функция 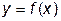имеет экстремум в этой точке.

Поскольку сплайн 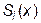– квадратичный, то он имеет единственную точку экстремума, абсцисса которой равна:

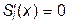
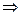
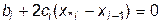
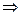
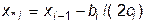. (10.9)

Для нас будет важен тот случай, когда эта точка окажется внутри частичного интервала, на котором определен данный сплайн, т.е. 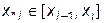. В противном случае, когда 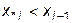, либо когда 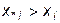, данная точка как точка экстремума для 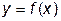нами рассматриваться не будет.

В качестве исследуемой функции взять зависимость 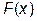из лабораторной работы № 3. Произвести вычисления для различных случаев разбиения общего интервала интерполирования. Например, при 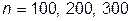и т.д., пока количество точек экстремума, определяемых Вашей программой не стабилизируется.

Пример выполнения лабораторного задания на Fortran

Воспользуемся уже разработанными компонентами из лабораторных работ № 3 и № 5, а в качестве исследуемой функции возьмем зависимость

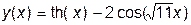. (10.10)

Стартуем среду разработки MS Visual Studio. Создадим новый проект LabTask_10f и сгенерируем в нем файл основной программной единицы – main_10.f90.

Пользуясь «Проводником», скопируем файлы, содержащие коды исследуемой функции (ЛР № 3) и метода Гаусса (ЛР № 5) в директорию проекта LabTask_10f и включим их в этот проект.

В данной лабораторной работе при решении СЛАУ нам не требуется вычислять determinant –определитель матрицы коэффициентов, поэтому мы удалим код, в котором он используется в процедуре Method_Gaussa(), а саму процедуру переименуем – SLAY (n, A1, B1, X).

Приступим к формированию файла модуля mod_10 для данной лабораторной работы – разместим в нем соответствующие интерфейсы и добавим в него описание нового типа (структуры) – spline, который мы будем использовать при организации данных, моделирующих программным путем квадратичные сплайны. Смысл записей данной структуры очевиден. Коэффициенты сплайна 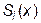обозначены через a, b, c, а поля xn и xk предназначены для «хранения» координат концов частичного отрезка 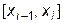, на котором этот сплайн определен.

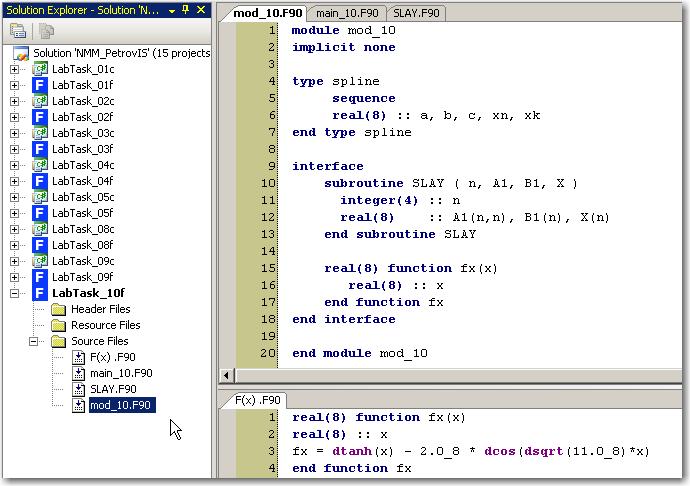
Ниже приведен код основной программы, с которым Вам необходимо разобраться самостоятельно:

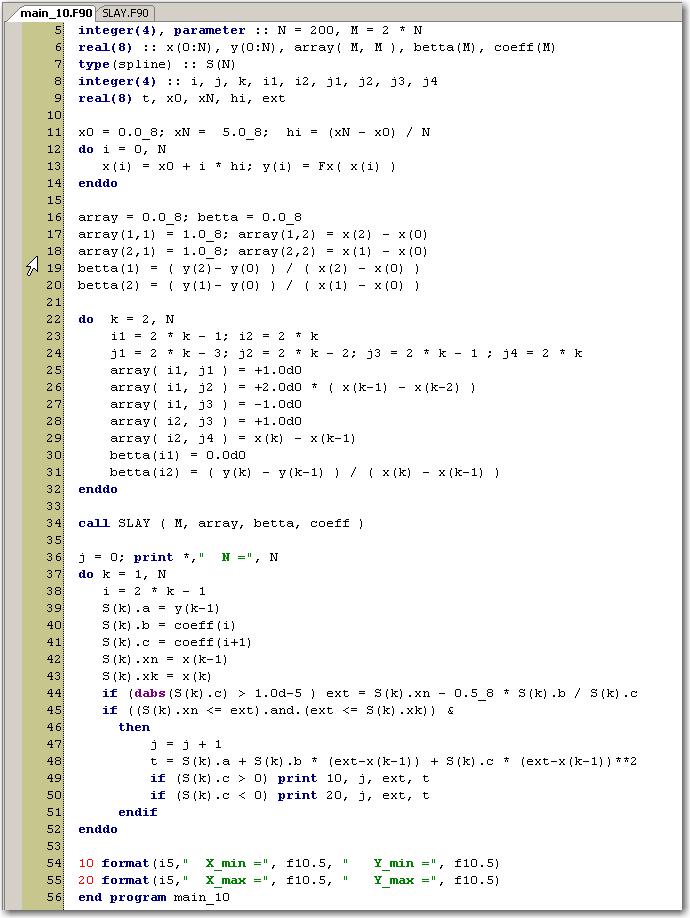
В отличие от предыдущих лабораторных работ, здесь мы используем статические массивы.

Поэтому для выполнения вычислений с различными значениями параметра N нам придется перекомпилировать программу. Такая схема работы, как правило, используется при отладке новых программ. Выполнение данного кода для N = 100 дает:

Если же задать N = 200 и запустить программу на выполнение возникнет аварийный останов со следующим сообщением:

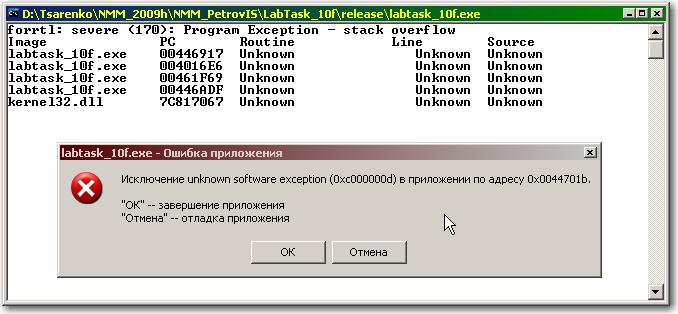
Причина программного прерывания – переполнение стека буферных операций. Оператор, вызвавший это прерывание, находится в строке 16 основной программы. Задание нулевых значений массиву array производится посредством буфера, размещенного в оперативной памяти (в стеке вызовов операторов ввода/вывода). По умолчанию его объем не превышает 1 МБ.

Мы не будем изменять код программы, а изменим свойства данного проекта и зададим новое значение для объема памяти, выделяемой под стек.

Откроем контекстное меню «Properties» для проекта LabTask_10f.

Откроем в нем пункт «Linker» и перейдем на подпункт «System». Затем, в таблице непосредственных свойств напротив свойства «Stack Reserve Size» зададим количество байт, которое мы посчитаем достаточным для нормальной работы программы, например, 16 МБ. Это число необходимо предварительно корректно вычислить при помощи стандартного калькулятора.

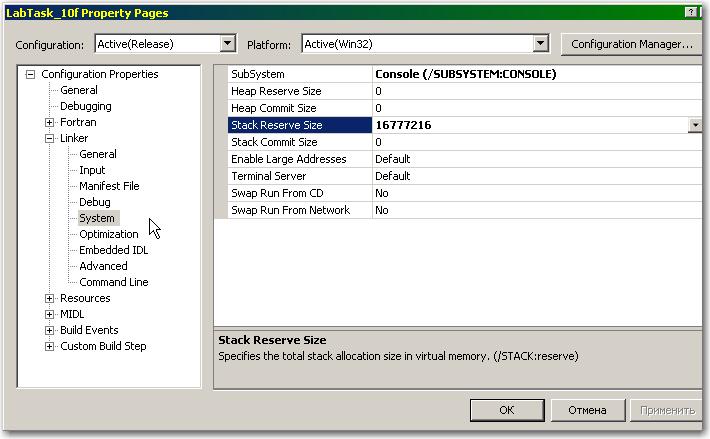
Перекомпилируем программу и запустим ее на выполнение при N = 200 и N = 300:

Сопоставление полученных результатов свидетельствует о том, что цель лабораторной работы достигнута – определены (с достаточной степенью точности) точки экстремума таблично заданной функции. Очевидно, что для более убедительного сравнения точек экстремума, полученных путем интерполирования сплайнами, с их точными значениями, необходимо выбирать тестовую функцию простого вида, например, 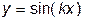или 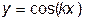. Рекомендуем выполнить такой анализ самостоятельно для различных значений параметра .

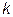Пример выполнения лабораторного задания на языке C#

В имеющемся рабочем пространстве NMM_PetrovIS сгенерируем (добавим) новый проект LabTask_10с консольного приложения на языке программирования C#, которому зададим тип конфигурации – Release, и который сделаем стартовым проектом.

Включим в проект новый класс – Class_10, в который скопируем из класса Class_05 подпрограмму Method_Gaussa(). Внесем изменения в код подпрограммы, связанные с исключением из нее вычислений определителя. После этого переименуем подпрограмму, например, так – SLAEq():

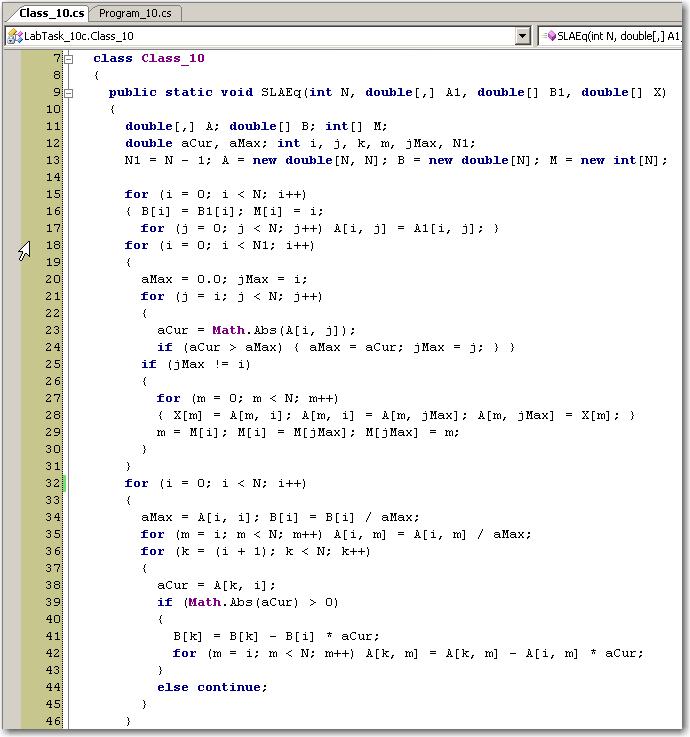
Добавим в этот класс функцию, которую нам предстоит исследовать (скопируем ее код из проекта LabTask_03с и переименуем):

В пространстве имен LabTask_10с определим новый тип данных – Spline2.

После этого приступим к составлению аналога на C# основной программной единицы main_10 на Fortran. Код программы может иметь, напрмер, следующий вид:

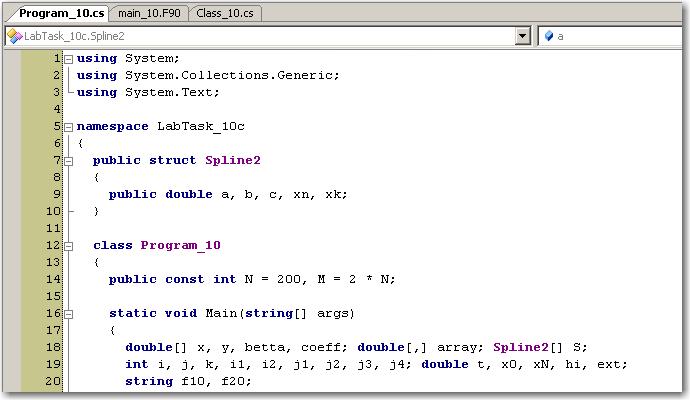
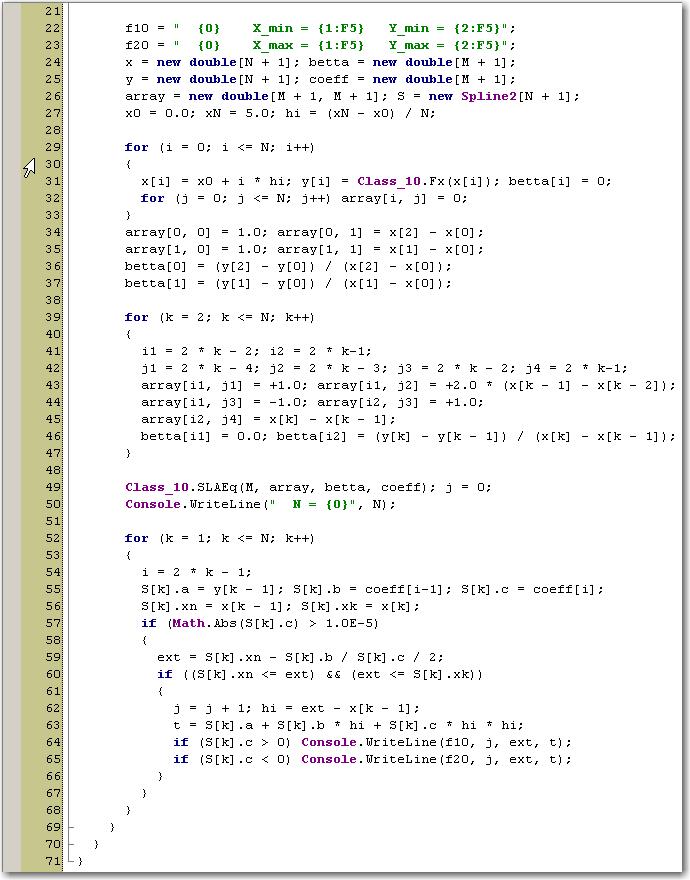
Выполним вычисления для случаев N = 100, 200 и N = 300:

Сопоставим результаты двух последних проектов и убедимся в их идентичности. Последнее свидетельствует в пользу того, что цель данной лабораторной работы достигнута.

Контроль выполнения варианта лабораторного задания № 10

Для контроля правильности Вашего выполнения лабораторной работы № 10 воспользуйтесь приложением NMM_Labs.

Выберите требуемую лабораторную работу и свой вариант. После этого – нажмите на кнопку «Выполнить» – перед Вами появится основная форма.

Работа пользователя с управляющими элементами данной формы начинается после нажатия на кнопку «Генерировать таблицу исходных данных».

Предварительно Вы можете выбрать «Количество интервалов интерполирования», например 15, которое при начальной загрузке имеет минимальное значение – 10:

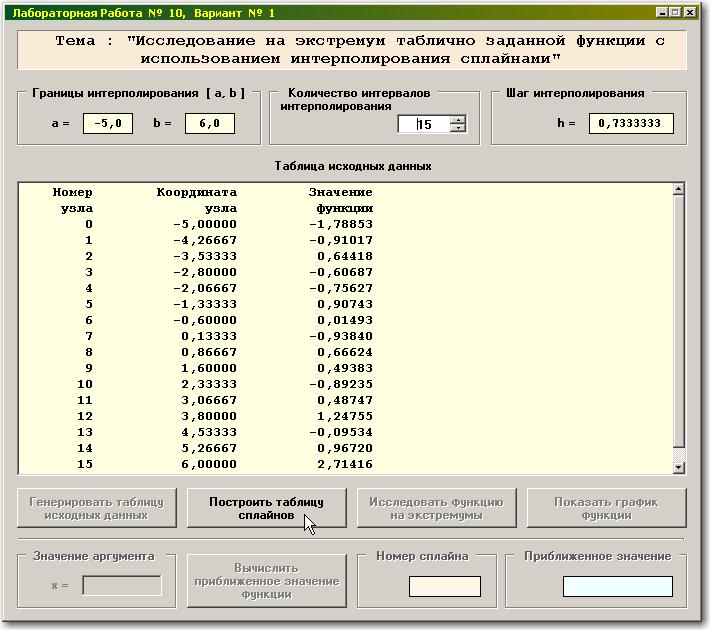
Полученная таблица будет использована в качестве «дискретно заданной функции», которую нам предстоит аппроксимировать при помощи системы сплайнов второго порядка, а затем исследовать на экстремум.

Таблица сплайнов будет построена сразу после нажатия на соответствующую кнопку:

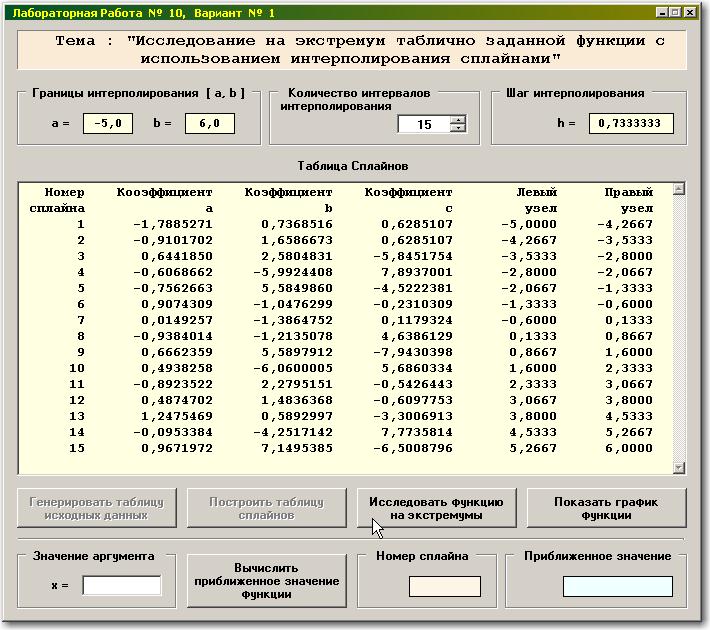
На основе построенной системы квадратичных сплайнов, аппроксимирующей дискретно заданную функцию, Вы можете выполнить ряд вычислительных операций.

Например, можно вычислить приближенное значение функции, задав значение аргумента и нажав на соответствующую кнопку.

При этом Вам будет не только предоставлено «Приближенное значение» функции, найденное посредством системы сплайнов, но и будет указан «Номер сплайна», непосредственно использованного при выполнении вычислений.

Следует помнить, что «Значение аргумента», задаваемое пользователем, должно удовлетворять основному условию интерполирования – оно не должно выходить за пределы «Границ интерполирования [a,b]», указанных в верхней части формы.

Основная задача лабораторной работы – исследование функции на экстремум – выполняется нажатием на соответствующую кнопку:

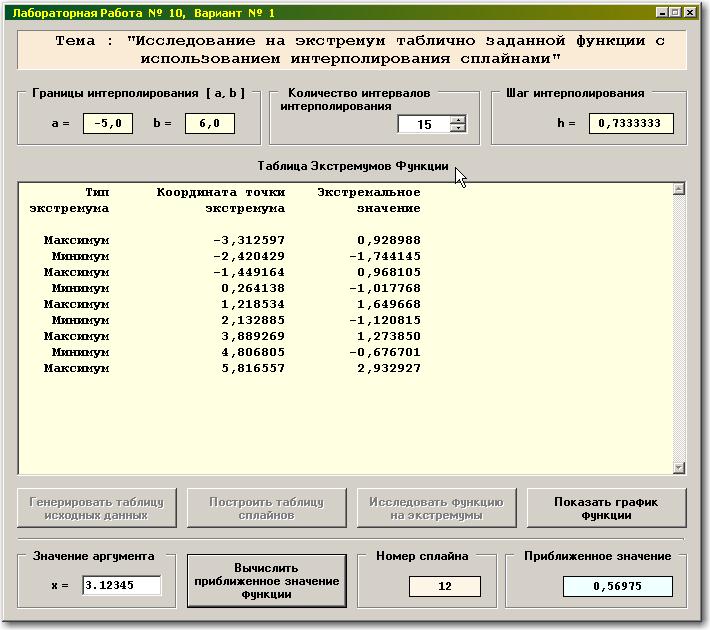
Данные из «Таблицы Экстремумов Функции» следует сравнить с аналогичными результатами, полученными при выполнении программ, непосредственно разработанных Вами (на Fortran и C#). Для этого необходимо задать соответствующее значение для параметра «Количество интервалов интерполирования», например – 100, и повторить все этапы вычислений.

В случае совпадения результатов (таблиц экстремумов функции) можно говорить об успешном завершении Вами данной лабораторной работы.

Понимание производимых математических действий при интерполировании сплайнами дискретных функций будет Вами усилено при помощи дополнительной возможности, предоставляемой программой NMM_Labs.

При малых значениях 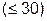параметра «Количество интервалов интерполирования» пользователю доступна кнопка «Показать график функции». Нажатие на эту кнопку генерирует новую форму с двумя графиками:

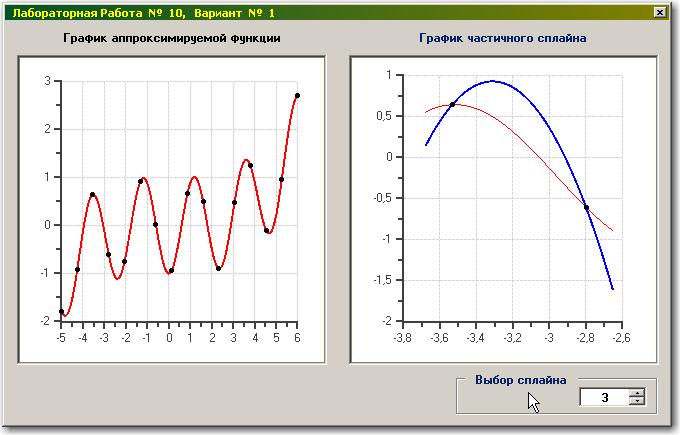
Правый график – «График аппроксимируемой функции». Он представляет собой непрерывную кривую красного цвета и изображает «истинную функцию», аналитический вид которой Вы использовали для построения дискретной функции (таблицы исходных данных).

Сама дискретная функция «накладывается» на эту кривую в виде точек черного цвета, что позволяет судить о «качестве» исходного дискретного представления нашей функции.

График слева – «График частичного сплайна». Здесь мы видим изображение квадратичного сплайна (кривая синего цвета), номер которого выбран на управляющем элементе.

Тонкая красная кривая – «истинная функция», аппроксимируемая данным сплайном на текущем интервале интерполирования. Здесь отчетливо видно качество интерполирования сплайном при выбранном количестве узлов таблицы исходных данных.

На приведенном графике можно визуально оценить погрешность, которая будет допущена при определении максимума функции на данном интервале интерполирования.

Последовательно увеличивая количество интервалов интерполирования, Вы можете проследить на данных графиках улучшение качества аппроксимации, как самой функции, так и ее экстремальных точек.

Дата добавления: 2014-12-24