Введение. (раздел «Алгоритмизация вычислительных процессов»)

Сборник задач

Е.И. Конопленко

По курсу «Информатика»

(раздел «Алгоритмизация вычислительных процессов»)

для студентов факультета

альтернативных форм обучения

Утверждено методической комиссией

__ ______ 2001 года

Москва 2001

Оглавление

Введение_________________________________________________________3

Линейные процессы________________________________________________4

Разветвляющиеся вычислительные процессы___________________________6

Циклические процессы:

табулирование ф-ций, нахождение максимума, минимума_______________8

табулирование ф-ций двух переменных______________________________10

вычисление сумм, произведений____________________________________12

Сложные циклы:

табулирование, вычисление сумм, произведений_____________________

табулирование, нахождение максимума и минимума___________________16

Одномерные массивы______________________________________________22

Двумерные массивы_______________________________________________23

Важным этапом в процессе решения задач на ЭВМ является этап алгоритмизации вычислительных процессов.

Сборник задач включает примеры для алгоритмизации всех вычислительных процессов: линейного, разветвляющегося, циклического.

Вычисление максимума и минимума, табулирование функции, вычисление суммы и произведения, сложные циклы, задачи на массивы – содержание сборника задач.

Составив блок-схему алгоритма решения задачи, студент, по указанию преподавателя, составляет программу на алгоритмическом языке, проводит отладку программы на ЭВМ, получает и анализирует результат решения.

Сборник, безусловно, будет полезен для самостоятельного решения, выполнения индивидуальных занятий студентам заочной формы обучения, а также студентам других форм образования.

Линейные процессы

Вариант	Пример
1.	Y = (|x| + sin^2x - 3) / 5x^3
2.	Y = sin(ax) + e^x + 2lnx
3.	Z = lny + y^1/3 + 3
4.	T = sin(x)^1/2 + 2ln|x| + 3x^2
5.	Z = arctg|x| + 2x^1/3 - cosx^2
6.	Y = sin|x^3| + 2x^1/2 + 2bx
7.	Z = cos^3x + ln|x| - abx
8.	Ф = arctgx^3 + asin|x| + x^1/2 - c
9.	Y = tgx^1/2 + e^2x - ablnx^3
10.	Z = sinax^2 + |cosx| + (ax)^1/3
11.	T = tgx^1/2+2cosax - x^1/2
12.	M = sin^2x + 2tgx^1/2 – 0.3ax
13.	Z = (x^1/2 + 2cos ^2x – e^x) / lnx^3
14.	A = (bcsinx^1/2 + 2x^3 – 3lnx) / arctgx^3
15.	Z = sinx^5 – 2x^1/3 + ablnx^1/2
16.	B = sin^2x + cosx^2 – ln^1/2x + e^x
17.	Z = (arctgx^3 + 2x^1/5 – sinx^2) / (2 + x^6)
18.	Y = cos^3x + 2sinx^1/2 + lnx
19.	Z = (lnx^3 + 2cosx^2 – 5x^1/2) / (sin^2x + 3)
20.	Y = x^3 + 2lnx – sin^2x – c
21.	Y = sinx^2 + tcos^2x – 3
22.	Z = siny – y^1/2 + 2a
23.	Z = lny – cosy + e^y – 3b
24.	Y = (x^3 + 2) / | x^1/2 + 3sinx |
25.	Y = x^1/2 + cosx - abx
26.	Y = sinax + e^x + 2lnx
27.	Y = x^1/2 + cos^2x + sinx^5 - 5
28.	Z = arctgy + 2asinx^1/2 + |x|
29.	Z = (acsin^2x + cos|x|) / (2tgx^2 + |x|)
30.	Y = (ac|x| - lnx^1/2) / (x^1/3 + 2sin^2x)
31.	C = e^x + 2/x^2 + 3cos^3x
32.	M = (lny^3 + |y| + 2sin^2y) / (2siny + y^5)
33.	A = (ey + 2y3 + y1/3) / (2siny + y5)
34.	B = (lnx + x1/2 + 2cx5) / (arctgx + |x|)
35.	C = (cos2x – sinx2 + |x|) / (x5 + ex – a)

Разветвляющиеся вычислительные процессы

N^o ^п./п.	Условие Задачи
Задача N^o1	Задача N^o2
1.	lLnx^1/2 + cos^2x x>3 Y = sinx^2 – 3 x<=3	y^1/3 + ey 1 <= y <= 2 Z = y + 2 3 < y <= 5. arctgy – y^1/3 y > 7
2.	sinx + 2^xx < 3 Y = x^3 + x1/2 x >= 3	y^3 + cos|y| - 2 y < 5 Z = y1/2 + lny 6 <= y <= 7 arctgy y > 7
3.	x + 3siny x > 3 Y = cos^2x – 3 x <= 3	ln^2y + y^1/3 – 3 y < 2 Z = cos^2y + siny^3 3 <y <=5 y + y^1/2 – e^y y > 7
4.	x + 3siny x > 3 Y = cos^2x – 3 x <= 3	y^3 + 2y – 3 y < 2 Z = lny^1/2 + 2 5 <= y < 6 y + tgy y > 6
5.	x^3 – 2lnx x > 3 Y = cosx^2 – 3 x >= 3	x + 2sinx – 3 1<=x<=2 Z = lnx^2 + x^1/3 3 < x <= 5 e^x + 3tgx x > 6
6.	x + sinx x < 3 Y = x^3 – x^1/3x >= 3	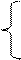cosx^2 – a x < 2 Z = lnx + e^x 3 <= x <= 5 x + 3 x > 7
7.	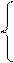lnx + 2sin^2x x > 2 Z = e^x – 3ax^1/2 x <= 2	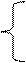sin^2x – 3 x < 2 Y = lnx^1/2 + 2c 3 < x <= 5 c^3 + e^x
8.	arctgy + 2ay y > 1 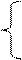Z = y^3 + sin^2y y <= 1	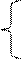e^x + |x| x < 3 Y = 2 – cos^3x 5 <= x < 7 lnx – c x > 9
9.	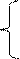arctgx + x^1/2x > 5 A = |x| + sin^3x x <= 5	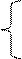cosx^1/2 + 2a 1 <= x < 2 Y = aclnx 5< x < 7 X^3 – 3 x > 10
10.	e^x + 2cos^3x x > 3 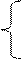Y = x^1/2 + 2cx^5x <= 3	e^x – 2ax 3 < x <= 5 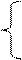Z = x^3 + |x| 7 < x < 8 cosx^1/2 + 3 x >= 9
11.	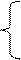lnx^3 + x^1/2 x > 3 Y = ax^2 – 3x^1/3 x <= 3	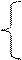lny + y^1/3 y < 3 Z = y^2 + 2siny 5 <= y <= 6 2ay y > 9
12.	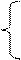y^5 + sin^3y – 1 y > 5 Z = e^x + a*ln(y) y <= 5	cos^2x + x^3 x < 2 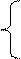Y = lnx +2 3 <= x <= 5 ab|x| x > 7
13.	sin^5x +cx^3 x > 2 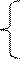Y = arctgx^1/2 – 3 x <= 2	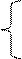siny^3 +2y y < 3 Z = |y| +a 5 <=y <= 6 lny^3 +y^1/2 y > 8
14.	lny^3 + y2 y > 3 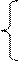Z = y^1/2 + 5 y <= 3	x^3 + sinx x < 3 Y = x^1/3 – 2a 5 <= x < 7 x^5 x > 8
15.	cosx + ax^3 x < 2 Y = arctgx – 3 x >= 2	y^5 + 2lny y < 2 Z = e^y – 3y 2.1<=y<=3.5 arctgy – 3 x > 5
16.	sin^3x + cosx^2 x > 5 A = x^5 + ln^1/2x x <= 5	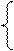a + e^x – 3 x < 1 Y = sin|x| + 5 2 <= x <= 3 arctgx – 2 x > 5
17.	arctgx^3 – 2a x<2 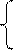B = lnx + cos^2x x>=2	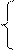x^1/2 + 5sinx x < 2 Y = x^5 – 3 3.5 < x <= 4 e^x + 2 x > 5
18.	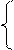ac*cos – 3 x > 1 Y = sin^2x + 5e^x y <= 1	arctgy + 2ay x < 5 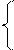Z = y^3 + e^y^2 6 <= y < 7 lny y > 8
19.	sin^2y + 2y^3 y > 2 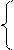Z = ln(siny) y <= 2	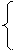arctgx + x^3 y < 3 Y = |x| - 2 4 <= x < 5 e^x + 3 x > 6
20.	ax^5 + x^1/3 x > 3 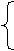Y = sinx + lnx x <= 3	x^5 + e^x x < 2 T = cos^3x + 2 3 <= x <= 4 arctgx + 5 x > 6
21.	arctgx^3 – 2x x > 5 B = cos^3x – 3a x <= 5	Sin^2x + 2x x < 2 Y = x^1/2 + x^1/5 – 3 3 <= x < 4 lnx + 5 x > 8
22.	sin^2x + cosx^2 x < 3 Z = x^1/2 – 3 x >= 3	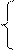sinx + 2x^1/2 x < 2 Y = lnx – 3 3 <= x < 4 x^5 + 5 x > 5
23.	lnx^3 + x^1/3 – 2 x < 2 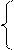A = arctgx x >= 2	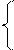arctgx^2 – x^1/2 x < 3 B = x^1/5 – 2 4 <= x <= 5 ln|x| + 2.5 6 < x < 7
24.	cost^3 – t^5 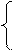t < 5 Ф = t + 3 t >= 5	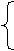sin^2x + cosx^2 x < 3 T = x^5 – 3 4 < x < 5 x^1/3 + 2 x > 6
25.	arctgx^2 – x^1/2x < 1 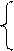M = a^5 + 2sin^2x x >= 1	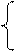x^3 + 2sinx x < 1 N = cosx^2 – 3 2 <= x < 3 ln|x| + 2 x > 5
26.	x^1/2 + x^1/3 – 3 x 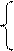< 2 C = ln|x| x >= 2	y^1/3 + e^y y < 2 B = y^5 + 2y^2 4 <= y <= 5 y^1/2 + 2siny y > 7

Дата добавления: 2014-12-24