Свойства дисперсии

Пошлины на яблоки.

Россия, являющаяся одним из крупных импортеров яблок, после вступления в ВТО почти наполовину снизит ввозные пошлины на эти фрукты. К 2017 году пошлина снизится еще в два раза. Пошлина на импорт груш к 2015 году уменьшится в два раза, свидетельствует документ об обязательствах РФ при вступлении во Всемирную торговую организацию (имеется в распоряжении "Интерфакса").

В настоящее время пошлина на ввоз яблок с 1 января по 31 июля составляет 0,1 евро/кг. С момента вступления России в ВТО (ожидается, что РФ станет фактическим членом организации до середины 2012 года) пошлина снизится до 0,06 евро/кг, а к 2017 году ее размер должен быть 0,03 евро/кг (на яблоки, поставляемые с 1 апреля по 30 июля - до 0,015 евро/кг). На 2013 год установлена ставка в размере 0,054 евро, на 2014 - 0,048 евро, на 2015 - 0,042 евро и на 2016 год - 0,036 евро. Аналогичная динамика снижения пошлин и на ввоз яблок с 1 апреля по 30 июля, кроме 2016 года, на который ставка пошлины составит 0,031 евро/кг.

Ставка пошлины на ввоз яблок с 1 августа по 31 декабря, которая в настоящее время составляет 0,1 и 0,2 евро/кг. (в зависимости от вида продукции), к 2017 году снизится до 0,06 и 0,03 евро/кг.

Согласно документу, к 2015 году Россия должна в два раза уменьшить пошлину и на ввоз груш, которая в настоящее время составляет 10% от таможенной пошлины. В момент присоединения к ВТО она сохранится на этом уровне, в 2013 году составит 8,3%, в 2014 году - 6,7%, в 2015 году - 5%.

Список литературы.

Приложение.

Приложение 1 Таблица 1

Средние потребительские цены на яблоки (на конец года; рублей за килограмм)

Цена на яблоки	27,59	31,48	31,72	34,09	36,87	44,09	48,62	56,33	53,51	62,37

Приложение 2 Таблица 2

Индексы потребительских цен на яблоки (декабрь к декабрю предыдущего года; в процентах)

Цена на яблоки	127,2	115,0	105,5	107,6	108,0	119,7	109,4	115,6	95,2	116,7

Приложение 3 Таблица 3

Индекс потребительских цен на яблоки (в процентах к предыдущему месяцу)

Январь	105,8	107,5	107,0	104,0	103,6	106,0	103,1	106,1	103,0	104,3
Февраль	102,6	101,6	102,5	101,7	102,4	105,1	101,0	104,7	102,9	101,2
Март	102,3	100,7	100,7	100,1	103,4	102,8	100,9	103,0	101,5	100,5
Апрель	101,8	100,7	100,3	99,8	104,1	100,4	101,3	104,9	100,0	99,4
Май	105,4	101,1	103,6	100,8	102,5	103,6	104,0	104,1	102,9	100,2
Июнь	107,0	102,2	104,5	103,9	100,8	102,5	104,0	102,6	101,1	99,7
Июль	99,9	98,9	100,7	101,7	95,3	101,2	99,2	98,3	101,2	99,7
Август	91,6	94,2	88,0	95,1	90,6	95,2	92,2	95,1	94,6	100,7
Сентябрь	96,4	96,7	94,4	94,9	95,1	97,1	95,9	96,0	93,6	101,9
Октябрь	102,4	101,4	99,3	98,7	101,3	99,7	100,4	99,0	95,2	101,0
Ноябрь	104,2	105,3	102,6	102,7	105,0	102,2	103,6	100,5	98,6	102,8
Декабрь	106,1	104,8	103,3	104,5	105,1	102,9	104,2	101,2	101,1	104,3

Приложение 4 Таблица 4

Соответствие потребительских цен на яблоки с ценой на говядину(на конец года в процентах)

	39,2	43,4

[1] Давидович Б. Борьба с бедностью в США // Экономист. 1994 - №4. – с.72-79.

1. Если все значения признака уменьшить (увеличить) на одну и ту же постоянную величину, то дисперсия от этого не изменится.
2. Если все значения признака уменьшить (увеличить) в одно и то же число раз n, то дисперсия соответственно уменьшится (увеличить) в n^2 раз.

Правило сложения дисперсии в статистике. Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий:

Смысл этого правила заключается в том, что общая дисперсия, которая возникает под влиянием всех факторов, равняется сумме дисперсий, которые возникают под влиянием всех прочих факторов, и дисперсии, возникающей за счет фактора группировки. Пользуясь формулой сложения дисперсий, можно определить по двум известным дисперсиям третью неизвестную, а также судить о силе влияния группировочного признака.

37. Среднее квадратическое отклонение случайной величины Х -квадратный корень из дисперсии. Теорема. Среднее квадратичное отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин. Пример. Завод выпускает 96% изделий первого сорта и 4% изделий второго сорта. Наугад выбирают 1000 изделий. Пусть Х – число изделий первого сорта в данной выборке. Найти закон распределения, математическое ожидание и дисперсию случайной величины Х. Выбор каждого из 1000 изделий можно считать независимым испытанием, в котором вероятность появления изделия первого сорта одинакова и равна р = 0,96. Таким образом, закон распределения может считаться биноминальным.

38. Квартильное отклонение. Правило 3 сигм. Квартильное отклонение. Половина разницы между третьим и первым квартилями. Иногда используется как "быстрая и приблизительная" оценка вариативности распределения, особенно когда медиана используется как измерение центральной тенденции. Также известно как полуинтерквантильное отклонение, при нормальном распределении оно равно вероятностной ошибке.

Правило трёх сигм

При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм.

Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины D:

Если принять D = 3s, то получаем с использованием таблиц значений функции Лапласа:

Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее квадратичное отклонение, практически равна нулю.

Это правило называется правилом трех сигм.

На практике считается, что если для какой – либо случайной величины выполняется правило трех сигм, то эта случайная величина имеет нормальное распределение.

39 Интенсивность вариации. Показатели размера и интенсивности вариации. Следующим этапом изучения вариации признака в совокупности является измерение характеристик силы, величины вариации. Простейшим из них может служить размах или амплитуда вариации - абсолютная разность между максимальным и минимальным значениями признака из имеющихся в изучаемой совокупности значений. Таким образом, размах вариации вычисляется по формуле

Поскольку величина размаха характеризует лишь максимальное различие значений признака, она не может измерять закономерную силу его вариации во всей совокупности. Предназначенный для данной цели показатель должен учитывать и обобщать все различия значений признака в совокупности без исключения. Число таких различий равно числу сочетаний по два из всех ед. совок-ти. Однако, нет необходимости рассматривать, вычислять и осреднять все отклонения. Проще использовать среднюю из отклонений отдельных значений признака от ср. арифметического значения признака. Но ср. отклонение значений признака от ср. арифметической величины согласно известному свойству последней = 0. Поэтому показателем силы вариации выступает не ср. арифметическая отклонений, а ср. модуль отклонений:

Ср. модуль, или ср. линейное отклонение, по абсолют. величине вычисляется как взвешенное по частоте отклонение по модулю середин интервалов от ср. арифметической величины, т.е. по ф-ле

Простота расчета и интерпретации составляют положительные стороны данного показателя, однако математические св-ва модулей «плохие»: их нельзя поставить в соответствие с каким-либо вероятностным законом, в том числе и с нормальным распределением, параметром которого является не ср. модуль отклонений, а ср. квадратическое отклонение. В стат-ой лит-ре ср. квадратическое отклонение от ср. величины принято обозначать малой греч. буквой сигма σ.

для ранжированного ряда

для интервального ряда

Ср. квадратическое отклонение по величине в реальных совокупностях всегда больше ср. модуля отклонений.

Понятие дисперсии. Квадрат ср. квадратического отклонения дает величину дисперсии. Формула дисперсии:

простая (для несгруппированных данных):

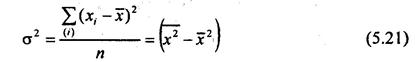
взвешенная (для сгруппированных данных):

На дисперсии основаны практически все методы математической статистики. Большое практическое значение имеет правило сложения дисперсий.

Еще одним пок-лем силы вариации, характеризующим ее не по всей совок-ти, а лишь в ее центральной части, служит ср. квартильное расстояние, т.е. ср. величина разности между квартилями:

Сила вариации в центральной части совок-ти, как правило, меньше, чем в целом по всей совок-ти. Соотношение между ср. модулем отклонений и ср. квартильным отклонением также служит для изучения структуры вариации: большое значение такого соотношения говорит о наличии слабоварьирующего «ядра» и сильно рассеянного вокруг этого ядра окружения. Для оценки интенсивности вариации и для сравнения ее в разных совокупностях и тем более для разных признаков необходимы относит. показатели вариации. Они вычисляются как отношения абсолют. показателей силы вариации, рассмотренных ранее, к ср. арифметической величине признака:

1) относительный размах вариации р:

2) относительное отклонение по модулю т:

3) коэффициент вариации как относительное квадратическое отклонение v:

4) относительное квартальное расстояние d:

где q - среднее квартильное расстояние.

Оценка степени интенсивности вариации возможна только для каждого отдельного признакам совокупности определенного состава. Так, для совокупности вариация может быть оценена как слабая, если v < 10%, умеренная при 10% < v < 25% и сильная при v > 25%.

Напротив, вариация роста в совокупности взрослых мужчин или женщин уже при коэффициенте, равном 7%, должна быть оценена и воспринимается людьми как сильная. Таким образом, оценка интенсивности вариации состоит в сравнении наблюдаемой вариации с некоторой обычной ее интенсивностью, принимаемой за норматив. Мы привыкли к тому, что урожайность, заработок или доход на душу, число жилых комнат в здании могут различаться в несколько и даже десятки раз, но различие роста людей хотя бы в полтора раза уже воспринимается как очень сильное.

Различная сила, интенсивность вариации обусловлены объективными причинами. Например, цена продажи доллара США в коммерческих банках Санкт-Петербурга на 24 января 1997 г. варьировала от 5675 до 5640 руб. при средней цене 5664 руб. Относительный размах вариации? = 35:5664 = 0,6%. Такая малая вариация вызвана тем, что при значительном различии курса доллара немедленно произошел бы отлив покупателей из «дорогого» банка в более «дешевые». Напротив, цена килограмма картофеля или говядины в разных регионах России варьирует очень сильно - на десятки процентов и более. Это объясняется разными затратами на доставку товара из региона-производителя в регион-потребитель.

40 Вариация альтернативного признака. Альтернативный признак — качественный признак, имею­щий две взаимоисключающие разновидности (например, работни­ки предприятия подразделяются на мужчин и женщин; продукция — на годную и бракованную и т. д.). Среди множества варьирующих признаков, изучаемых статистикой, существуют признаки, которыми обладают одни единицы совокупности и не обладают другие. Эти признаки называются альтернативными. Альтернативный признак принимает всего два значения — 0 и 1 с весами соответственно p и q. Поэтому среднее значение альтернативного признака равно р. А дисперсия альтернативного признака равна pq. Дисперсия альтернативного признака равна произведению доли признака, обладающего характеристикой на долю признака, не обладающего характеристикой. Предельное значение дисперсии для альтернативного признака равно 0,25 при р=0,5. Дисперсия альтернативного признака широко применяется в выборочном обследовании.

44. Показатели тесноты связи между признаками. Шкала Чеддока. Коэф. Детерминации. Показатели тесноты связи дают возможность охарактеризовать степень зависимости вариации результативного признака от вариации признака - фактора. К простейшим показателям тесноты связи относится коэффициент корреляции знаков (коэффициент Г. Фехнера), основанный на оценке степени согласованности направлений отклонений индивидуальных значений факторного и результативного признаков от соответствующей средней. Основан на степени согласованности направлений отклонений индивидуальных значений факторного и результативного признаков от соответствующих средних величин. Для расчета этого показателя исчисляют средние значения факторного и результативного признаков (по арифметической простой), а затем проставляют знаки отклонений для значений взаимосвязанных пар признаков: если фактическое значение признака больше средней величины, то ставится знак «+», если меньше – то знак «-». Коэффициент Фехнера определяется по формуле:

где С – количество совпадений знаков;

Н – количество несовпадений знаков.

Коэффициент Фехнера может принимать любые значения в пределах 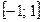. Если К_ф= 1, то это значит, что знаки всех отклонений совпадают; если знаки всех отклонений будут разными, то К _ф =0. Если К _ф =-1, то это дает возможность предположить наличие обратной связи. Этот показатель позволяет уловить направление связи, но не учитывать точно ее величину.

Если знаки всех отклонений совпадут то и - свидетельствует о наличие прямой связи, если все знаки не совпадают, тогда и - наличие обратной связи.

Коэффициент детерминации ( - R-квадрат) — это доля дисперсии зависимой переменной, объясняемая рассматриваемой моделью зависимости, то есть объясняющими переменными. Более точно — это единица минус доля необъяснённой дисперсии (дисперсии случайной ошибки модели, или условной по факторам дисперсии зависимой переменной) в дисперсии зависимой переменной. Его рассматривают как универсальную меру связи одной случайной величины от множества других. В частном случае линейной зависимости является квадратом так называемого множественного коэффициента корреляции между зависимой переменной и объясняющими переменными. В частности, для модели парной линейной регрессии коэффициент детерминации равен квадрату обычного коэффициента корреляции между y и x. Истинный коэффициент детерминации модели зависимости случайной величины y от факторов x определяется следующим образом:

где — условная (по факторам x) дисперсия зависимой переменной или дисперсия случайной ошибки модели.

В данном определении используются истинные параметры, характеризующие распределение случайных величин. Если использовать выборочную оценку значений соответствующих дисперсий, то получим формулу для выборочного коэффициента детерминации (который обычно и подразумевается под коэффициентом детерминации):

где -сумма квадратов остатков регрессии, - фактические и расчетные значения объясняемой переменной.

- общая сумма квадратов.

В случае линейной регрессии с константой 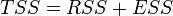, где — объяснённая сумма квадратов, поэтому получаем более простое определение в этом случае — коэффициент детерминации — это доля объяснённой суммы квадратов в общей:

Необходимо подчеркнуть, что эта формула справедлива только для модели с константой, в общем случае необходимо использовать предыдущую формулу.

Иногда показателям тесноты связи можно дать качественную оценку (шкала Чеддока):

Количественная мера тесноты связи	Качественная характеристика силы связи
0,1-0,3	Слабая
0,3-0,5	Умеренная
0,5-0,7	Заметная
0,7-0,9	Высокая
0,9-0,99	Весьма высокая

Функциональная связь возникает при значении равном 1, а отсутствие связи - 0. При значениях показателей тесноты связи меньше 0,7 величина коэффициента детерминации всегда будет ниже 50%. Это означает, что на долю вариации факторных признаков приходится меньшая часть по сравнению с остальными неучтенными в модели факторами, влияющими на изменение результативного показателя. Построенные при таких условиях регрессионные модели имеют низкое практическое значение.

Дата добавления: 2014-12-24