Метод выборочного наблюдения, его сущность и преимущество. Виды выборки. Определение необходимой численности выборки. Особенности малых выборок

Выборочное наблюдение – это такое несплошное наблюдение, при котором отбор подлежащих обследованию единиц осуществляется в случайном порядке, отобранная часть изучается, а результаты распространяются на всю исходную совокупность. Наблюдение организуется таким образом, что эта часть отобранных единиц в уменьшенном масштабе представляет всю совокупность. Совокупность, из которой производится отбор, называется генеральной, и все ее обобщающие показатели – генеральными. Совокупность отобранных единиц именуют выборочной совокупностью, и все ее обобщающие показатели – выборочными. Основная задача выборочного наблюдения в экономике состоит в том, чтобы на основе характеристик выборочной совокупности (средней и доли) получить достоверные суждения о показателях средней и доли в генеральной совокупности. При этом возникают ошибки двух видов: регистрации и репрезентативности. Ошибки регистрации могут иметь случайный (непреднамеренный) и систематический (тенденциозный) характер. Случайные ошибки обычно уравновешивают друг друга, поскольку не имеют преимущественного направления в сторону преувеличения или преуменьшения значения изучаемого показателя. Систематические ошибки направлены в одну сторону вследствие преднамеренного нарушения правил отбора. Ошибки репрезентативности присущи только выборочному наблюдению и возникают в силу того, что выборочная совокупность не полностью воспроизводит генеральную. Они представляют собой расхождение между значениями показателей, полученных по выборке, и значениями показателей этих же величин, если бы они были получены при сплошном наблюдении. Для каждого конкретного выборочного наблюдения значение ошибки репрезентативности может быть определено по соответствующим формулам, которые зависят от вида, метода и способа формирования выборочной совокупности. По виду различают индивидуальный, групповой и комбинированный отбор. При индивидуальном отборе в выборочную совокупность отбираются отдельные единицы генеральной совокупности; при групповом отборе – качественно однородные группы или серии изучаемых единиц; комбинированный отбор предполагает сочетание первого и второго видов. По методу выборки различают повторную и бесповторную выборки. При повторной выборке общая численность единиц генеральной совокупности в процессе выборки остается неизменной. Ту или иную единицу, попавшую в выборку, после регистрации снова возвращают в генеральную совокупность, и она сохраняет равную возможность со всеми прочими единицами при повторном отборе единиц вновь попасть в выборку. При бесповторной выборке единица совокупности, попавшая в выборку, в генеральную совокупность не возвращается и в дальнейшем в выборке не участвует. Т.о., при бесповторной выборке численность единиц генеральной совокупности сокращается в процессе исследования. Способ отбора определяет конкретный механизм или процедуру выборки единиц из генеральной совокупности. На практике выборочных исследований наибольшее распространение получили следующие виды выборки: собственно-случайная, механическая, типическая, серийная, комбинированная. К собственно-случайной выборке относится отбор единиц из всей генеральной совокупности (без предварительного расчленения ее на какие-либо группы) посредством жеребьевки (преимущественно) или какого-либо иного подобного способа, например, с помощью таблицы случайных чисел. Случайный отбор – это отбор не беспорядочный. Принцип случайности предполагает, что на включение или исключение объекта из выборки не может повлиять какой-либо фактор, кроме случая. Механическая выборка состоит в том, что отбор единиц в выборочную совокупность из генеральной, разбитой по нейтральному признаку на равные интервалы (группы), производится таким образом, что из каждой такой группы в выборку отбирается лишь одна единица. Чтобы избежать систематической ошибки, отбираться должна единица, которая находится в середине каждой группы. Для отбора единиц из неоднородной совокупности применяется так называемая типическая выборка, которая используется в тех случаях, когда все единицы генеральной совокупности можно разбить на несколько качественно однородных, однотипных групп по признакам, влияющим на изучаемые показатели. Серийная выборка предполагает случайный отбор из генеральной совокупности не отдельных единиц, а их равновеликих групп (серий) с тем, чтобы в таких группах подвергать наблюдению все без исключения единицы. Комбинированная выборка заключается в объединении различных способов выборки, рассмотренных ранее.

13;14. Средняя и предельная ошибка выборки. Методика их расчёта для средней и доли. Оценка существенности расхождения выборочных средних.

Основные характеристики параметров генеральной и выборочной совокупностей обозначаются символами: N – объем генеральной совокупности (число входящих в нее единиц); n – объем выборки (число обследованных единиц); - генеральная средняя (среднее значение признака в генеральной совокупности); - выборочная средняя; p – генеральная доля (доля единиц, обладающих данным значением признака в общем числе единиц генеральной совокупности); w – выборочная доля. Доля выборки есть отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности: 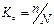. Применяя выборочный метод в статистике, обычно используют два основных вида обобщающих показателя: среднюю величину количественного признака и относительную величину альтернативного признака (долю или удельный вес единиц в статистической совокупности, которые отличаются от всех других единиц этой совокупности только наличием изучаемого признака). Выборочная доля (w), или частость, определяется отношением числа единиц, обладающих изучаемым признаком т, к общему числу единиц выборочной совокупности п: w = т / п. Для характеристики надежности выборочных показателей различают среднюю и предельную ошибки выборки. Ошибка выборки 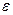или, иначе говоря, ошибка репрезентативности представляет собой разность соответствующих выборочных и генеральных характеристик: для средней количественного признака 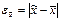; для доли (альтернативного признака) . Выборочная средняя и выборочная доля являются случайными величинами, которые могут принимать различные значения в зависимости от того, какие единицы совокупности попали в выборку. Поэтому определяют среднюю из возможных ошибок – среднюю ошибку выборки.

Средняя ошибка выборки при повторном отборе рассчитывается по следующим формулам: для средней количественного признака: ; для доли (альтернативного признака): . Средняя ошибка выборки при бесповторном отборе рассчитывается по следующим формулам: для средней качественного признака ; для доли (альтернативного признака) . В каждой конкретной выборке расхождение между выборочной средней и генеральной 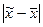может быть меньше средней ошибки , равно ей или больше ее. Причем каждое из этих расхождений имеет различную вероятность. Поэтому фактические расхождения между выборочной средней и генеральной можно рассматривать как некую предельную ошибку, связанную со средней ошибкой и гарантируемую с определенной вероятностью Р. Предельную ошибку выборки можно рассчитать по следующим формулам: при повторном отборе: для средней , где t – нормированное отклонение – «коэффициент доверия», зависящий от вероятности, с которой гарантируется предельная ошибка выборки; 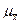- средняя ошибка выборки; для доли 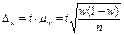; при бесповторном отборе: для средней ; для доли . При вероятности 0,683 коэффициент t = 1; при вероятности 0,954 коэффициент t = 2; при вероятности 0,997 коэффициент t = 3. Предельная ошибка выборки позволяет определить предельные значения характеристик генеральной совокупности и их доверительные интервалы: для средней 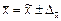; ; 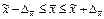для доли ; . Наряду с абсолютным значением предельной ошибки выборки рассчитывается также и предельная относительная ошибка выборки, которая определяется как процентное отношение предельной ошибки выборки к соответствующей характеристике выборочной совокупности: для средней, %: ; для доли, %: .

15. Виды и формы взаимосвязей социально-экономических явлений. Корреляционная связь, её особенности, методы выявления и оценки тесноты.

Статистическое изучение связи можно разделить на три этапа: 1. Это качественный анализ, который связан с анализом природы социального или экономического явления. Этот анализ проводится либо методами экономической теории или методами социологии. 2. Это построение модели связи. Базируется на статистических методах. Это способ группировки. 3. Инторпритация полученных результатов. Связан с качественными особенностями изучаемого явления.

Между различными явлениями и их признаками необходимо прежде всего выделить два типа связей: функциональную и статистическую. Связь признака y с признаком x называется функциональной связью y=f(x). Эта связь жёсткая детермированная f(x_i)= f(x_j). X – факторный признак, Y – результативный признак. Чаще всего функциональные связи наблюдаются в явлениях описываемых математикой, физикой и другими точными науками. Имеют место эти связи и в социально-экономических науках. Стохастическая связь – это связь между величинами, при которой одна из них, случайная величина y, реагирует на изменение другой величины x или других величин x1,x2,…,xn, измененм закона распределения. Характерной особенностью стохастических связей является то, что они проявляются во всей совокупности, а не в каждой её единице. Модель стохастической связи может быть представлена в общем виде уравнением: y_i=f(x_i)+E_i. f(x_i) – это часть результативного признака, сформулированного под влиянием нашего факторного признака x. E – часть результативного признака, который возник по действием неучтённых факторов, кроме x. Частным случаем стохастической связи является Корреляционная связь - существует там, где взаимосвязанные явления характеризуются только случайными величинами. При такой связи среднее значение случайной величины результативного признака закономерно изменяется в зависимости от изменения другой величины или других случайных величин. Корреляционная связь проявляется не в каждом отдельном случае, а во всей совокупности в целом.

Связи классифицируются: по направлению (прямые – направление изменения результативного признака совпадает с направлением изменения признака-фактора и обратные); по аналитическому выражению (линейные – с возрастанием значений факторного признака происходит непрерывное возрастание значений результативного признака, нелинейные, криволинейные – с возрастанием значения факторного признака возрастание результативного признака происходит неравномерно); по степени тесноты связи, степень тесноты определяется по величине коэффициента корреляции (слабые и тесные).

Дата добавления: 2014-12-24