Средняя арифметическая величина

Средняя арифметическая, Средняя гармоническая, Средняя геометрическая.

Понятие средней арифметической

Виды средних величин различаются прежде всего тем, какое свойство, какой параметрисходной варьирующей массы индивидуальных значений признака должен быть сохраненнеизменным.

Средней арифметической величиной называется такое среднее значение признака, привычислении которого общий объем признака в совокупности сохраняется неизменным.

Иначе можно сказать, что средняя арифметическая величина -среднее слагаемое. При еевычислении общий объем признака мысленно распределяется поровну между всеми единицамисовокупности. Например, средняя заработная плата или средний доход работниковпредприятия - это такая сумма денег, которая приходилась бы на каждого работника, если бывесь фонд оплаты труда (или все доходы, направленные на личное потребление) былраспределен между работниками поровну.

Исходя из определения, формула средней арифметической величины имеет вид:

Средняя арифметическая

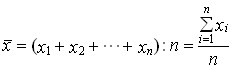, (5.1)

где х? - средняя величина;

п – численность совокупности.

По формуле (5.1) вычисляются средние величины первичных (объемных) признаков, еслиизвестны индивидуальные значения признака. Если изучаемая совокупность велика, исходнаяинформация чаще представляет собой ряд распределения или группировку, как, например,табл. 5.1.

Таблица 5.1

Распределение футбольных матчей высшей лиги России по числу забитых за матч обеимикомандами мячей в 1996 г.

Число забитых мячей,х											Итого
Число матчей, fi

Среднее число мячей, забитых за одну игру, должно представлять собой результатравномерного распределения общего числа забитых мячей по всем 306 матчам розыгрышапервенства. Общее число забитых мячей, согласно исходной информации табл. 5.1, можнополучить как сумму произведений значений признака в каждой группе хi, на число игр с такимколичеством забитых мячей fi (частоты). Получим формулу (5.2)

,

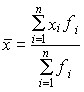где п — число групп.

Такую форму средней арифметической величины называют взвешенной арифметическойсредней в отличие от простой средней, рассчитанной по формуле (5.1). В качестве весоввыступают здесь числа единиц совокупности в разных группах. Название «вес» выражает тотфакт, что разные значения признака имеют неодинаковую «важность» при расчете среднейвеличины. «Важнее», весомее число забитых мячей, которое встречалось чаще: 1, 2, 3 мяча, атакие значения, как 7 или 9 забитых мячей, как бы ни радовались таким результативнымматчам болельщики, при расчете средней не играют большой роли: их «вес» мал.

Имеем: х? = 802: 306 = 2,62 мяча за игру.

Как видим, средняя арифметическая величина может быть дробным числом, если дажеиндивидуальные значения признака могут принимать только целые значения (дискретныйпризнак). Ничего «предосудительного» для метода средних в этом не заключено; из сущностисредней не вытекает, что она обязана быть реальным значением признака, которое могло бывстретиться у какой-либо единицы совокупности.

Виды средней арифметической

Если при группировке значения осредняемого признака заданы интервалами, то при расчетесредней арифметической величины в качестве значения признака в группах принимаютсередины этих интервалов, т.е. исходят из гипотезы о равномерном распределении единицсовокупности по интервалу значений признака. Для открытых интервалов в первой и последнейгруппе, если таковые есть, значения признака надо определить экспертным путем исходя изсущности, свойств признака и совокупности. Например, по табл. 5.2 можно минимальный возрастрабочих считать 17 лет. Тогда первый интервал будет от 17 до 20 лет, а максимальный возраст- 65 лет, тогда последний интервал - 50-65 лет.

Таблица 5.2

Распределение рабочих предприятия по возрасту

Группы рабочих повозрасту, лет	Число рабочих fj	Середина интервала х'j	xjfj
До 20		18,5
20-30
30-40
40 - 50
Старше 50		57,5
Итого		34,56

Средний возраст рабочих, рассчитанный по формуле (5.2) с заменой точных значений признака вгруппах серединами интервалов, составил:

что и записано в итоговую строку по графе 3 табл. 5.2. Напомним, итог объемного показателя —это сумма, итогов по графе относительных показателей или средних групповых величин —средняя. Числитель дроби - это общая сумма человеко-лет, прожитых рабочими предприятия;разделив ее на число работников, получаем возраст в годах, так что логика показателясредней величины соблюдена.

Перейдем к рассмотрению средних вторичных (относительных) признаков. Сумма такихпоказателей сама по себе реальной величиной какого-либо признака в совокупности неявляется. Однако общее определение арифметической средней сохраняет силу и в этом случае.При вычислении таких средних величин необходимо, чтобы сохранялась сумма величиныобъемного признака, который является числителем при построении осредняемогоотносительного показателя. Например, при вычислении средней величины урожайностикакой-либо сельскохозяйственной культуры (по формуле (5.2)) необходимо, чтобы общий объемвалового сбора этой культуры остался неизменным при замене индивидуальных величинурожайности средней величиной. Нельзя менять реальную величину объемного признака - онаявляется базой расчета средней. Чтобы выполнить указанное условие, в качестве весов прирасчете средней величины относительного показателя необходимо принять значения тогопризнака, который является знаменателем при определении относительного показателя. Так,при вычислении средней урожайности по совокупности хозяйств весами должны служитьразмеры площади данной культуры.

Рассмотрим пример расчета средней доли предметов народного потребления в общем выпускепромышленной продукции по совокупности предприятий (табл. 5.3). В этом случае весом долженявляться общий объем всей продукции предприятия.

Тогда средняя доля предметов народного потребления в продукции четырех предприятийравна: х = (615,5: 2047) • 100% = 30,07%. Средняя доля ближе к долям у тех предприятий,которые имеют большой объем всей продукции (предприятия № 2 и 3). Числитель среднейвеличины 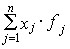- это объем выпуска предметов потребления всеми предприятиями -величина, которая должна сохраняться неизменной при замене разных четырех долей насреднюю долю. Расчет по данным табл. 5.3 проведен на основе известных индивидуальныхзначений осредняемого признака и весов.

Таблица 5.3

Объем и структура промышленной продукции

Номера предприятий	Объем всей продукции, млн руб., fj	Доля товаров народногопотребления, % xj,	Объем выпуска товаров народногопотребления, млн руб., xj fj
1 138 75 103,5 2 650 38 247,0 3 1040 12 124,8 4 219 64 140,2
Итого 2047 30,07 615,5

Однако исходная информация может иметь другую форму: индивидуальные значенияосредняемого признака могут быть неизвестны, зато известны индивидуальные или суммарныезначения объемных признаков как числителя, так и знаменателя относительной величины.Например, известно, что в акционерном сельхозпредприя-тии было посажено 145 га картофеляи собрано с них 2595,5 т продукции. При этом совершенно неизвестно, сколько было собрано скаждого гектара из 145 га в отдельности, хотя на самом деле, конечно, индивидуальныевеличины продукции, полученные на каждом гектаре, существовали объективно. Однаконикакой потребности в их раздельном учете нет; учет продукции ведется по бригадам, поотдельным полям севооборота, но не по каждому гектару. Среднюю урожайность картофеляполучают попросту делением массы собранной продукции на площадь посадки, т. е. какотносительную величину, характеризующую хозяйство в целом:

По отношению к предприятию это относительный показатель. Но существуют и сами значенияурожайности с каждого из 145 га, хотя и неучтенные. По отношению к ним 17,9 т с 1 га - этосредняя величина. Такую форму определения средней арифметической величины, при которойостаются неизвестными индивидуальные значения осредняемого признака, следует называтьНеявной формой средней. Формула такой средней имеет вид:

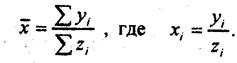
Свойства арифметической средней величины

Знание некоторых математических свойств средней арифметической полезно как при ееиспользовании, так и при ее расчете.

1. Сумма отклонений индивидуальных значений признака от его среднего значения равна нулю.

Доказательство:

Примечание. Для взвешенной средней сумма взвешенных отклонений равна нулю.

Попробуйте доказать это самостоятельно.

2. Если каждое индивидуальное значение признака умножить или разделить на постоянноечисло, то и средняя увеличится или уменьшится во столько же раз.

Доказательство:

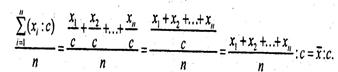
Вследствие этого свойства индивидуальные значения признака можно сократить в с раз,произвести расчет средней и результат умножить на с.

3. Если к каждому индивидуальному значению признака прибавить или из каждого значениявычесть постоянное число, то средняя величина возрастет или уменьшится на это же число.

Доказательство:

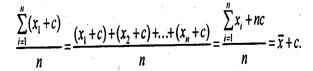
Это свойство полезно использовать при расчете средней величи-ны из многозначных ислабоварьирующих значений признака, например роста группы лиц: х1 = 179 см; х2 = 183 см; х3= 171 см; х4 = 180 см; х 5= 169 см. Для вычисления среднего роста из каждого значениявычитаем 170 см и находим среднюю из остатков:

(9+ 13 + 1 + 10 - 1): 5 = 6,4. Средний рост = 6,4 + 170 = 176,4 см.

4. Если веса средней взвешенной умножить или разделить на постоянное число, средняявеличина не изменится.

Доказательство:

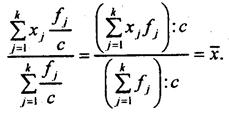
Используя это свойство, при расчетах следует сокращать веса на их общий сомножитель либовыражать многозначные числа весов в более крупных единицах измерения.

В табл. 5.4 приведен пример комплексного использования свойств средней арифметической дляоблегчения расчетов.

Таблица 5.4

Расчет средней продуктивности коров на ферме

Группы коров по надою за год, кг хj	Число Коров fj	Середина интервала, кг, x’j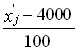
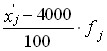
3000 – 3400 43 3200 - 8 - 344 3400 - 3800 71 3600 - 4 - 284 3800-4200 102 4000 0 0 4200-4600 64 4400 4 256 4600 - 5000 27 4800 8 216
Итого 307 - - -156

Средний надой молока на корову находим так:

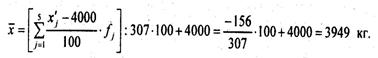
5. Сумма квадратов отклонений индивидуальных значений признака от среднейарифметической меньше, чем от любого другого числа.

Доказательство. Составим сумму квадратов отклонений от переменной а:

Чтобы найти экстремум этой функции, нужно ее производную по а приравнять нулю:

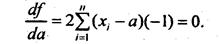
Отсюда имеем:

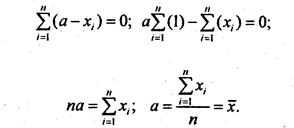
Таким образом, экстремум суммы квадратов отклонений достигается при а = х. Так каклогически ясно, что максимума функция не может иметь, этот экстремум является минимумом.

Применение простой и взвешенной средней

Простая и взвешенная средние величины различаются не только по величине (не всегда), поспособу вычисления, но и по своей роли в решении различных задач статистического анализа.Рассмотрим, например, среднюю величину урожайности картофеля в группе хозяйств. Если этасредняя при решении поставленной задачи входит в систему показателей площади посадки,валового сбора, себестоимости, суммы затрат и других характеристик производства, тоследует применять взвешенную среднюю, так как произведение невзвешенной средней наобщую сумму площадей не даст суммы валового сбора.

Если же нас интересуют такие задачи, как измерение вариации урожайности между хозяйствамиили связь урожайности с дозой органических удобрений, то следует применять простуюсреднюю величину урожайности, полностью абстрагируясь от размеров площадей посадки.Иначе на полученный результат повлияют различия площадей, совершенно не касающиесяэтого признака. Точно так же, если необходимо изучить колебания урожайности за ряд лет ивыявить их связь с температурой июня и суммой осадков за лето, нужно применять простуюсреднюю урожайность за ряд лет, абстрагируясь от различия размеров площадей в разныегоды.

Чтобы правильно применять средние величины, следует знать, от каких причин зависитразличие между простой и взвешенной средними. Рассмотрим этот вопрос на примереарифметической средней. Пусть x? - простая средняя, х?z - взвешенная средняя, в которойвесами выступают значения признака z, п - число единиц совокупности. Отклоненияиндивидуальных значений признака хi от простой средней х? обозначим?xi = хi - х?. Отклоненияпризнака веса?zi = zi -z?. Тогда индивидуальные значения признаков х и z можно выразитьчерез их средние и отклонения: хi = х? +?xi; zi = z? +?zi, а взвешенную среднюю х,представить в виде

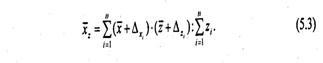
Перемножим величины в скобках и просуммируем почленно, имея в виду, что . Средние величины можно вынести за знак суммирования, какконстанты. Получим:

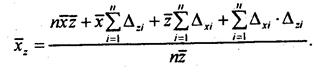
Так как суммы отклонений индивидуальных значений признака от средней арифметическойсогласно первому ее свойству равны нулю, то второе и третье слагаемые числителя такжеравны нулю.

Остается:

Числитель второго слагаемого в формуле (5.4) - это числитель коэффициента корреляции междуосредняемым и весовым признаками (см. формулы 8.11 и 8.14). Подставив выражениекоэффициента корреляции /^ в (5.4), получим:

Итак, средняя арифметическая взвешенная равна простой средней плюс произведение среднегоквадратического отклонения ос-редняемого признака на коэффициент вариации весовогопризнака и на коэффициент корреляции между этими признаками. Если обе части равенства (5.5)разделить на простую среднюю х, получим:

(О среднем квадратическом отклонении и коэффициенте вариации см. ниже в этой главе.)

Из (5.5) следует, что взвешенная средняя равна простой в трех случаях:

• а) если не варьирует изучаемый признак,?х = 0 - тривиальная ситуация, когда и сами средниене нужны;

• б) при условии, что не варьирует признак-вес vz = 0;

• в) в случаях, когда между осредняемым и признаком-весом нет линейной корреляции, rxz = 0.

Взвешенная средняя больше простой, если эта корреляция прямая. Взвешенная средняя меньшепростой средней, если эта корреляция обратная.

8. Структурные средние: мода и медиана.

Мода -величина признака, т.е. варианта, которая наиболее часто повторяется в совокупности.

Модой называется то значение признака, которая соответствует максимальной точке, теоретической кривой распределения.

Мода отражает типичный, наиболее расп распространенный вариант значения признака.
Если данные не сгруппированы, то моду определяют согласно определению.
Мода = ∑x*f

В дискретном ряду распределения мода-варианта, кот.соответствует наибольшей частоте.
В интервальном ряду расп. сначала определяют модальный интервал(интервал содержащий моду)-ему соответствует наиб.частота.

Мо = xm+imo*((fmo-fmo-1)/ (fmo-fmo-1)+(fmo-fmo+1)),
xm-нижнее значение модального интервала
imo-величина мод.интервала
fmo-частота модального интервала
fmo-1-частота предыдущего интервала
fmo+1-частота следующего интервала

Значение моды в этом случае приблизительно, т.к. ее значение зависит от величины групп, от границы интервалов и т.д.

Моду можно определить графически

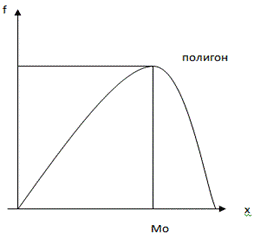
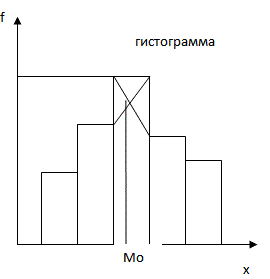
Медиана-величина, которая делит численность упорядоченного вариационного ряда на две равные части. Одна часть имеет значение не больше, чем медиана, а другая-не меньше, чем медиана.

Для ранжированного ряда с нечетным числом членов, медианой является варианта расположенная в центре. Номер варианты определяется по формуле
NMe= (n+1)/2

Для ранжированного ряда с четным числом, медиана рассчитывается, как среднеарифметическое из 2-х вариантов, расположенных в центре.

n=2k k=n/2
Me=(xk+ xk+1)/ 2

Для дискретного ряда распределения медиана рассчитывается с помощью накопленных частот. Медианой является варианта, кот.соответствует накопленная частота впервые превысившая половину общей суммы частот.
Для интервального ряда сначала, с помощью накопленных частот определяют медианный интервал, которому соответствует накопленная частота, впервые превысившая половину суммы частот. Затем конкретное значение медианы определяют:

Me = xme+ime*((∑f/2-Sme-1)/ fme),

xme-нижнее значение медианного интервала
ime-величина медианного интервала
Sme-1-сумма накопленных частот для интервала предшествующего медианному.

Дата добавления: 2014-12-24