
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Среднее квадратичное отклонение и дисперсия случайной величины
|
|
|
|
Пример 2. Найдем математическое ожидание случайных величин 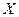 и
и  , зная законы их распределения
, зная законы их распределения
1)
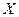
| -8 | -4 | -1 | |||
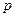
| 
| 
| 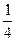
| 
| 
| 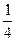
|
2)

| -2 | -1 | ||||
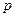
| 
| 
| 
| 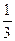
| 
| 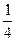
|
Решение:
 ,
,
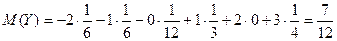 .
.
|
 Получили любопытный результат: законы распределения величин
Получили любопытный результат: законы распределения величин 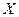 и
и  разные, а их математические ожидания одинаковы.
разные, а их математические ожидания одинаковы.
|
Из рисунка б видно, что значение величины  более сосредоточены около математического ожидания
более сосредоточены около математического ожидания 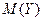 , чем значения величины
, чем значения величины 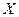 , которые разбросаны (рассеяны) относительно ее математического ожидания
, которые разбросаны (рассеяны) относительно ее математического ожидания  (рисунок а).
(рисунок а).
Основной числовой характеристикой степени рассеяния значений случайной величины 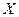 относительно ее математического ожидания
относительно ее математического ожидания  является дисперсия, которая обозначается через
является дисперсия, которая обозначается через 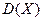 .
.
Определение. Отклонением называется разность между случайной величиной 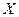 и ее математическим ожиданием
и ее математическим ожиданием  , т.е.
, т.е. 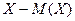 .
.
Отклонение 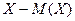 и его квадрат
и его квадрат 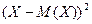 также являются случайными величинами.
также являются случайными величинами.
Определение. Дисперсией дискретной случайной величины 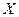 называется математическое ожидание квадрата ее отклонения:
называется математическое ожидание квадрата ее отклонения:
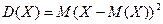 .
.
Свойства дисперсии.
1. Дисперсия постоянной величины С равна 0:
 .
.
2. Если 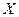 - случайная величина, а С – постоянная, то
- случайная величина, а С – постоянная, то
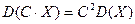
 .
.
3. Если 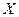 и
и  - независимые случайные величины, то
- независимые случайные величины, то
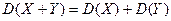 .
.
Для вычисления дисперсий более удобной является формула
 .
.
Пример 3. Дискретная случайная величина распределена по закону:
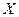
| -1 | |||
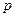
| 0,2 | 0,1 | 0,3 | 0,4 |
Найти 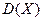 .
.
Решение. Сначала находим  .
.
 ,
,
а затем  .
.
 .
.
По формуле  имеем
имеем
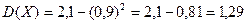 .
.
Средним квадратичным отклонением случайной величины называется корень квадратный из ее дисперсии:
 .
.
|
|
|
|
|
Дата добавления: 2014-12-24; Просмотров: 557; Нарушение авторских прав?; Мы поможем в написании вашей работы!