Аналитические показатели ряда динамики

Сопоставимость уровней и смыканий рядов динамики

На сопоставимость уровней ряда динамики непосредственно влияет методология учета или расчета показателей. Периодизации динамики - процесс выделения однородных этапов развития. Характеристика рядов динамики в зависимости от расстояния между уровнями: 1) с равностоящими уровнями; 2) с неравностоящими уровнями во времени. Равностоящие ряды динамики - ряды динамики одинаковых периодов, или следующих через равные промежутки времени показателей. Неравностоящие ряды динамики - ряды с неровными периодами или неравномерными промежутками между датами. Основное условие правильного построения ряда динамики - сопоставимость всех входящих в него уровней. Смыкание рядов динамики - объединение в одни ряд (более длинный) двух или нескольких рядов динамики, уровни которых исчислены по разной методологии или разным территориальным границам. Условия смыкания рядов; необходимо, чтобы по одному из периодов (переходному) имелись данные, исчисленные по разной методологии (или в разных границах).

Рядами динамики называются ряды расположенных в хронологическом порядке показателей, характеризующих изменение какой-либо величины во времени. Ряды динамики включают два основных элемента: показатели времени - t и соответствующие им показатели величины - Y. 1. Абсолютный прирост. Разность значений двух показателей ряда динамики. Базисный абсолютный прирост - разность текущего значения и значения принятого за постоянную базу сравнения: . Цепной абсолютный прирост - разность текущего и предыдущего значений: 2. Темп роста. Отношение двух уровней ряда (может выражаться в процентах). Базисный темп роста - отношение текущего значения и значения принятого за постоянную базу сравнения: 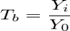Цепной темп роста - отношение текущего и предыдущего значений: 3. Темп прироста. Отношение абсолютного прироста к сравниваемому показателю. Базисный темп прироста - отношение абсолютного базисного прироста и значения принятого за постоянную базу сравнения:
. Цепной темп прироста - отношение абсолютного цепного прироста и предыдущего значения показателя: 4. Ускорение. Абсолютное ускорение - разница между абсолютным приростом за данный период и абсолютным приростом за предыдущий период равной длительности. Измеряется только цепным способом . Относительное ускорение - отношение цепного темпа прироста за данный период и цепного темпа прироста за предыдущий период . 5. Темп наращивания. Отношение цепных абсолютных приростов к уровню, принятому за постоянную базу сравнения: 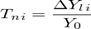. 6. Абсолютное значение одного процента прироста
Отношение абсолютного прироста к темпу прироста, выраженное в процентах.
После раскрытия формула упрощается до . Для получения обобщающих характеристик динамики изучаемого ряда рассчитываются средние показатели динамики.

Дата добавления: 2014-12-24