Предмет математической статистики 2 страница

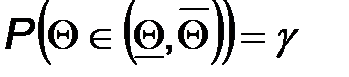
Как правило, в качестве доверительной вероятности выбирают достаточно близкое к единице значение. Стандартными являются следующие значения доверительной вероятности:

Такие значения для 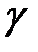выбираются для того, чтобы получать информацию об изучаемом параметре с вероятностью близкой к единице, т.е. почти наверняка. В связи с этим иногда доверительную вероятность называют надежностью.

Замечание. Иногда вместо доверительной вероятности (надежности) использую величину 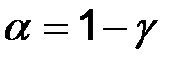, называемую уровнем значимости.

Построение доверительного интервала для математического ожидания нормального распределения при известном .

Пусть наблюдаемый признак Х распределен по нормальному закону и известно его среднее квадратическое отклонение .

Рассмотрим случайную величину

где а - математическое ожидание Х.

Теорема. Случайная величина z распределена по нормальному закону с параметрами 0,1.

При доказательстве несмещенности выборочного среднего было показано, что 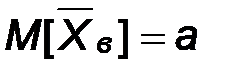, поэтому

.

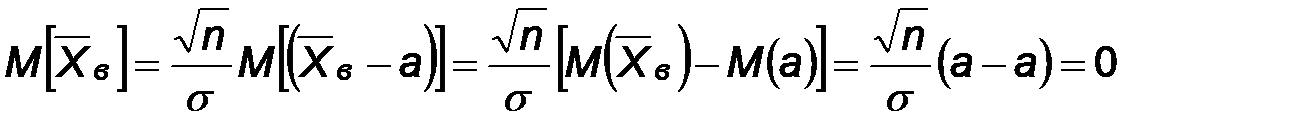Покажем, что . В самом деле,

Теорема доказана.

Обозначим через решение уравнения

.

Функция задается таблично и решение выписанного уравнения также определяется при помощи таблиц. При этом следует учитывать, что функция нечетна, т.е., что .

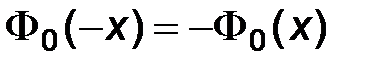Найдем теперь вероятность того, что 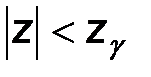. Поскольку случайная величина z распределена по нормальному закону с параметрами 0,1, имеем:

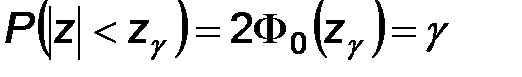
С другой стороны, неравенство 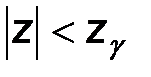эквивалентно следующим:

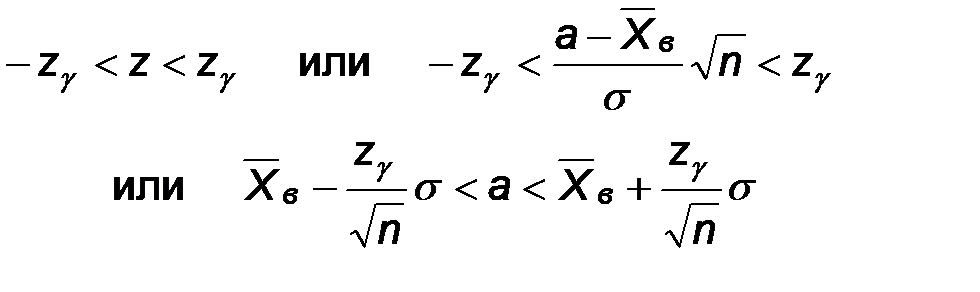
Следовательно, .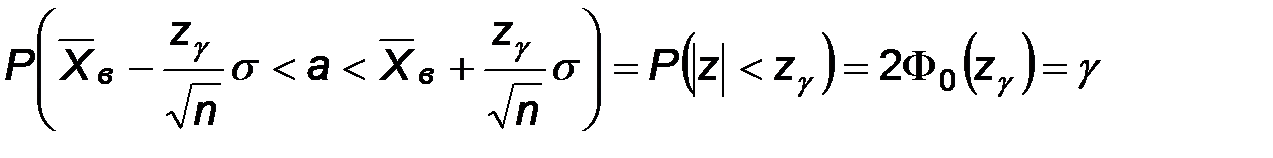

По определению доверительного интервала имеем, что интервал

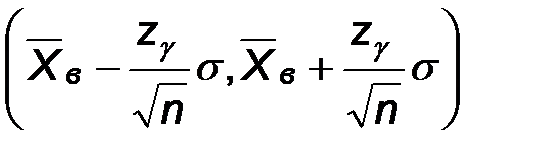
является доверительным для математического ожидания с доверительной вероятностью .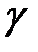

Замечание. Доверительную вероятность называют иногда надежностью. Кроме того, вместо надежности 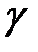задают иногда уровень значимости , связанный с надежностью соотношением .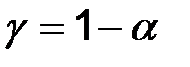

Пример. Случайная величина Х имеет нормальное распределение со средним квадратическим отклонением 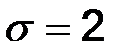. Найти доверительный интервал по выборке 2,1; 2,3; 2,4; 2,6; 2,8; 2,7; 2,5;2,.4; 2,7; с уровнем значимости 0,05.

Доверительная вероятность (надежность) в рассматриваемом случае такова .

Найдем , решив уравнение .

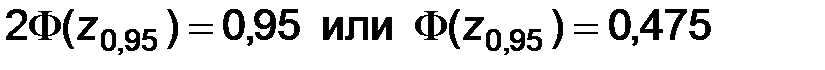Пользуясь таблицами для функции , получаем .

Очевидно объем выборки в рассматриваемом случае n=9.

Найдем :

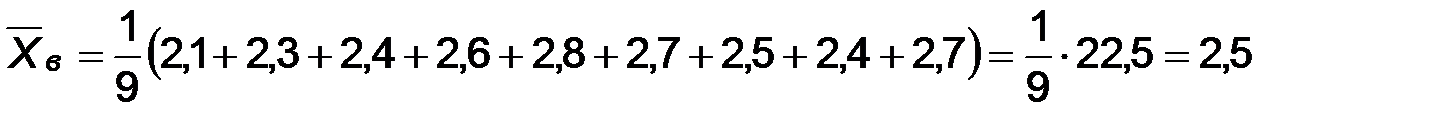
Следовательно, искомый доверительный интервал имеет вид:

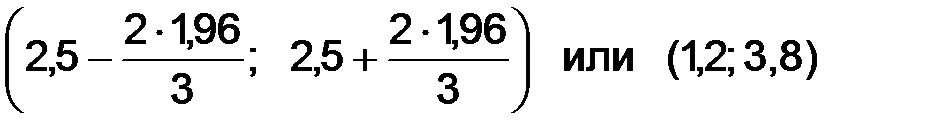
Построение доверительного интервала для математического

ожидания нормального распределения при известном .

Пусть - выборка объема из генеральной совокупности признака Х, распределенного по нормальному закону.

Случайная величина называется распределенным по закону Стьюдента (t - распределение) c k=n-1 числом степеней свободы.

Для этой случайной величины составлен в виде таблицы закон распределения, который называют t – распределением Стьюдента.

При помощи этих таблиц может быть решена задача нахождения по заданному 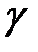значения , удовлетворяющее уравнению:

.

Величина оказывается зависящей от 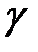и числа степеней свободы k=n-1 и, поэтому в дальнейшем, обозначается . В таблице находится на пересечении столбца соответсвующего 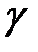= 0,95; 0,99; 0,995; и строки, указывающей число степеней свободы.

Рассмотрим неравенство .

Это неравенство эквивалентно следующему , отсюда

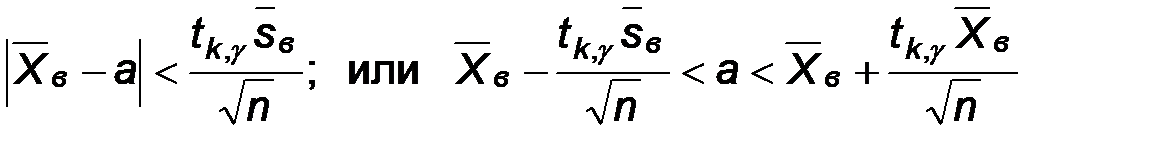
Поскольку все записанные неравенства эквивалентны, то

.

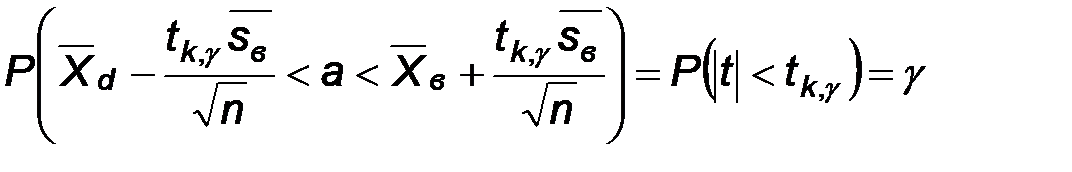Последнее означает, что интервал является доверительным, соответствующим надежности .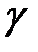

Пример. Случайная величина Х имеет нормальное распределение. Найти доверительный интервал для математического ожидания по выборке: 5, 6, 4, 6, 7, 4, 8, 7, 9, 4 с уровнем значимости 0,05.

По выборке находим .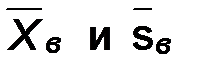

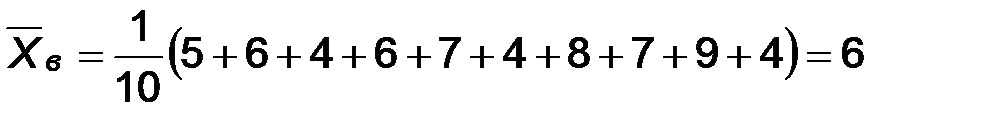
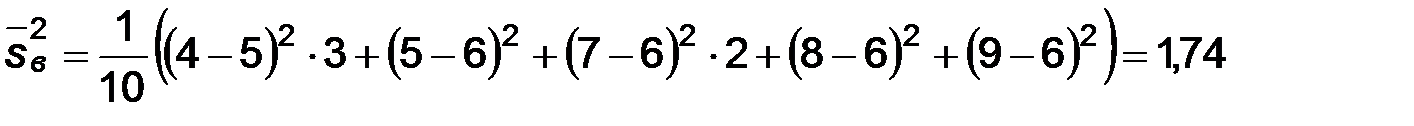
Найдем по таблице

Следовательно, искомый интервал имеет вид

.

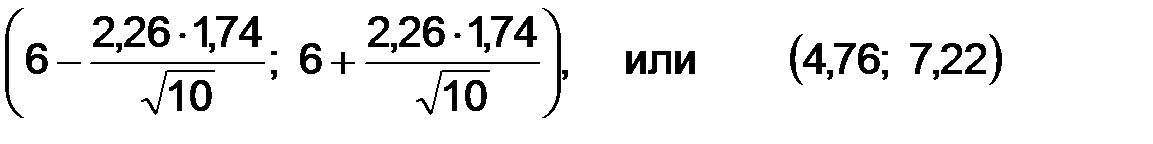Проверка статистических гипотез.

Под статистической гипотезой будем понимать всякое высказывание о наблюдаемом признаке, которое может быть проверено по результатам выборки.

Пусть - закон распределения наблюдаемого признака Х, зависящий от параметра, истинное значение которого нам неизвестно.

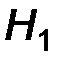Предположим, что нам необходимо проверить гипотезу . Назовем эту гипотезу нулевой и будем обозначать через . Гипотезу , состоящую в том, что 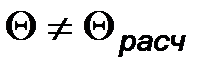, назовем конкурирующей или альтернативной.

Нашей задачей является по статистическим данным (по выборке) из гипотез и 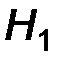принять какую-либо и, следовательно, отвергнуть альтернативную гипотезу. При этом мы можем совершать следующие ошибки:

1. Гипотеза отвергается, но является верной. Такую ошибку назовем ошибкой первого рода.

2. Гипотеза принимается, но является неверной. Такую ошибку назовем ошибкой второго рода..

Схематически решение сформулированной задачи состоит в следующем: в зависимости от вида гипотезы по выборке рассчитывают некоторую величину, называемую статистикой. Это значение называют расчетным значением статистики (). С другой стороны, статистику подбирают так, что для нее известно, так называемое, теоретическое значение (), определяемое по известному виду распределения. Расчетное и теоретическое значения статистики сравниваются и при этом если, в некотором смысле, они мало отличаются, то нет оснований отвергать гипотезу, а если различия между теоретическим значением статистики и ее расчетным значением существенны, то нулевая гипотеза отвергается. Как правило, сравнение указанных величин состоит в проверке выполнения неравенств: 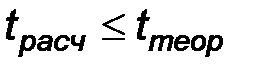или 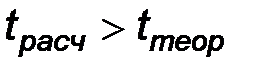. Тем самым множество выборок разбивается на 2 непересекающихся подмножества. Одно из них называется областью допустимых значений и описывается неравенством 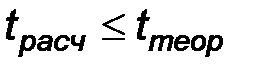, а второе называется критической областью и описывается неравенством 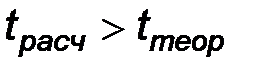. Область допустимых значений обозначают, как правило, через 0, а критическую область – через W.

Проверка гипотезы о равенстве центров распределения двух

нормальных генеральных совокупностей при известных дисперсиях.

Пусть Х и Y – два наблюдаемых признака, подчиненных нормальному распределению. Будем считать, что дисперсии известны. Будем считать, что выборки независимы. Тогда выборочные средние также независимы и распределены по нормальному закону. Это означает, что и разность распределена по нормальному закону. 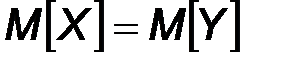Найдем параметры распределения этой случайной величины, предполагая, что гипотеза , состоящая в том, что , верна. Тогда

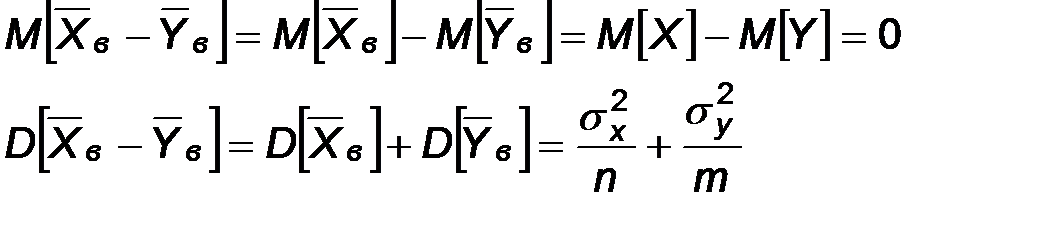
Последние равенства означают, что случайная величина распределена по нормальному закону с параметрами (0, 1).

Пользуясь статистикой z, построим критическую область и область допустимых значений для гипотез:

Пусть задана вероятность , с которой мы принимаем решение о совпадении центров, т.е. гипотезу . При этом величина называется уровнем значимости.

Рассмотрим уравнение

.

Решением этого уравнения будет 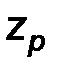находится по таблицам для нормального распределения.

Последнее означает, что область допустимых значений описывается неравенством:

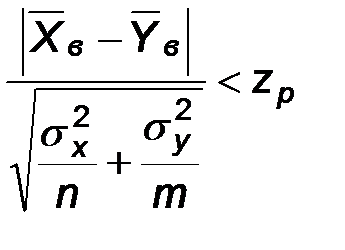или .

Следовательно, в рассматриваемом случае критическая область задается неравенством:

.

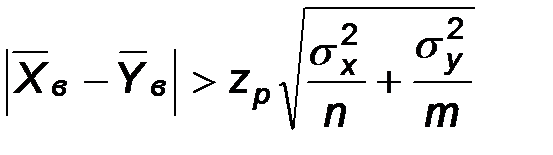Пример. По результатам выборок двух наблюдаемых признаков, распределенных по нормальному закону с дисперсиями , , проверить гипотезу о совпадении центров, приняв уровень значимости .

X: 2,1; 2,2; 2,3; 2,15; 2,4; 2,5; 2,4; 2,3; 2,1; 2,2

Y: 2,3; 2,4; 2,8; 2,0; 2,0; 2,6; 2,7; 2,8; 2,9; 3,0; 2,9

Выполним необходимые расчеты:

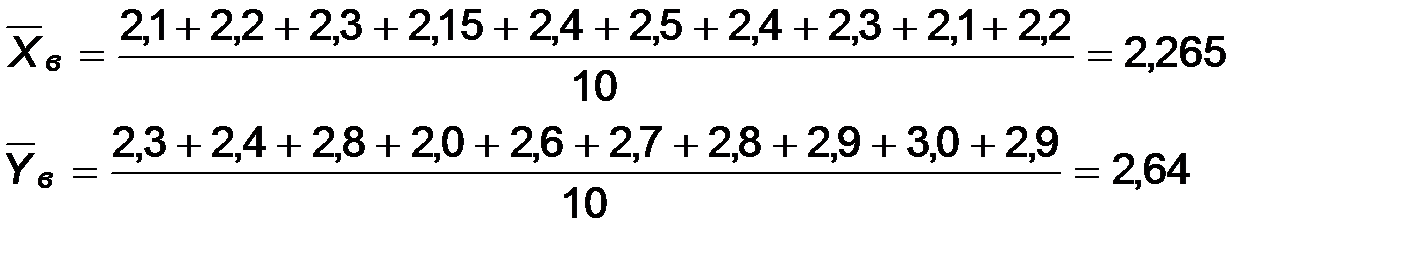
Поэтому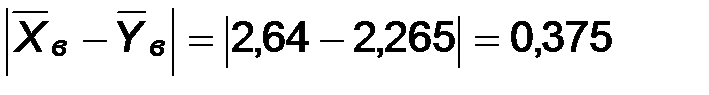
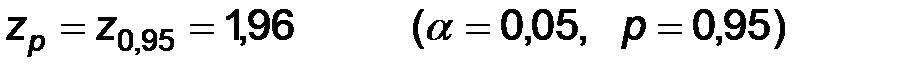
, а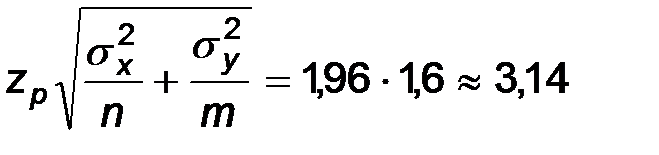

Так как 0,375<3,14, то выборка принадлежит области допустимых значений и нет оснований отвергать гипотезу о равенстве центров наблюдаемых признаков.

Проверка гипотез о законе распределения.

Критерий согласия .

Пусть Х – наблюдаемый признак и требуется проверить гипотезу , состоящую в том, что Х подчиняется закону распределения F(x).

Произведем выборку объема n; и построим по этой выборке эмпирическую функцию распределения F*(х).

Проверка гипотезы :состоит в сравнении законов F(х) и F*(х) при помощи, так называемого, критерия согласия. Существует много различных критериев согласия. Мы рассматриваем один из них – критерий согласия .

Разобьем генеральную совокупность признака Х на l интервалов 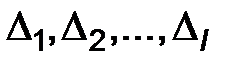и подсчитаем число элементов, попавших на каждый из этих интервалов.

Предполагая, что гипотеза имеет место, можно найти вероятности 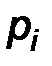попадания случайной величины в интервал . Тогда теоретическое значение числа элементов, попавших в интервал , есть .

Результаты расчетов помещаем в следующую таблицу:

Интервалы			…
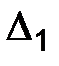
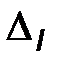
Эмпирические частоты			…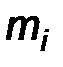
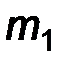
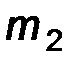
Теоретические частоты			…

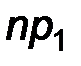
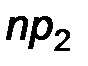
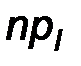
По построению .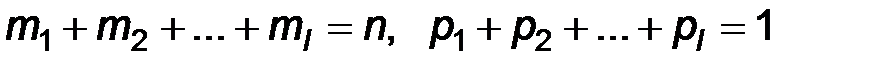

Рассмотрим следующую статистику

Можно показать, что эта статистика имеет распределение с k=l-r-i числом степеней свободы. Здесь r – число параметров, входящих в функцию F(x).

Значение может быть найдено при помощи таблицы по числу степеней свободы k и заданному уровню значимости .

С другой стороны, может быть найдено расчетное значение по приведенной выше формуле.

Область допустимых значений в рассматриваемом случае описывается неравенством: , а критическая область – неравенством .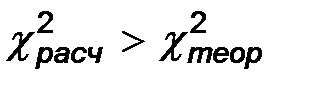

Пример. При уровне значимости 0,05, проверить гипотезу о нормальном распределении генеральной совокупности, если выборка представлена интервальным рядом частот.

Интервалы	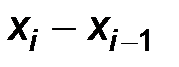1,2-2,2	2,2-3,2	3,2-4,2	4,2-5,2	5,2-6,2	6,2-7,2
Частоты

Для проверки о нормальном распределении с помощью критерия согласия , необходимо найти теоретические частоты.

1.Перейдем от интервального распределения к статистическому ряду распределения частот признака Х. В качестве представителя каждого интервала берем значение

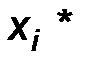
	1,7	2,7	3,7	4,7	5,7	6,7

2.Вычисляем

3.Нормируем случайную величину Х, т.е. переходим к величине z

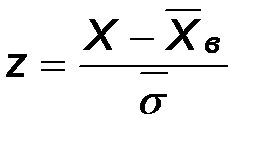
и вычисляем концы интервалов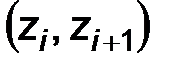

причем, наименьшее значение z полагают равным -¥, а наибольшее +¥.

4.Вычисляем теоретические вероятности 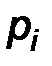попадания в интервал по формуле , и находим искомые теоретические частоты .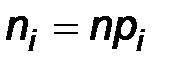

5.Вычисляем . Вычисления удобно проводить с помощью следующих таблиц.

№1.

№
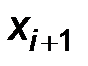
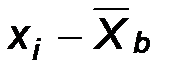
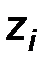
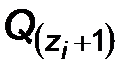
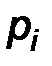
	1,2	2,2	-	-1,3	-¥	-1,17	-0,5	-0,379	0,1210	24,20
	2,2	3.2	-1,3	-0,3	-1,17	-0,27	-0,379	-0,1064	0,2726	54,52
	3,2	4.2	-0,3	0,7	-0,27	0,63	-0,1064	0,2357	0,3421	68,42
	4,2	5.2	0,7	1,7	0,63	1,53	0,2357	-0.4370	0,2013	40,26
	5,2	6.2	1,7	2,7	1,53	2,43	0,4370	0,4290	0,0550	11,0
	6,2	7.2	2,7	3,7	2,43	¥	0,4920	0,5	-,0050	1,6

№2.

№			-
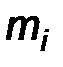
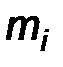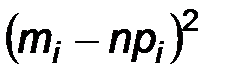
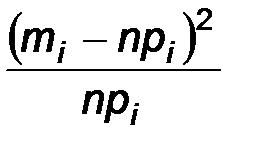
		24,2	-5,2	27,04	1,11
		54,52	9,48	89,67	1,64
		38,42	2,58	6,55	0,09
		40,26	-9,26	85,74	2,12
		11,0			0,09
		1,6	1,4	2,36	1,47

Находим по таблице – число степеней свободы у нас k=6-2-1-3, уровень значимости 0,05.

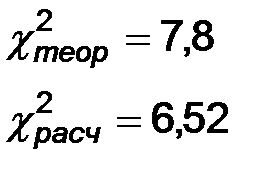
Так как 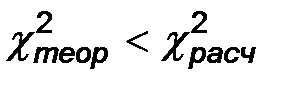- нет оснований отвергать гипотезу о нормальном распределении.

Дата добавления: 2014-12-24