Оценка генеральной дисперсии по исправленной выборочной дисперсии

Получим несмещенную оценку для генеральной дисперсии 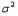: Def: Статистику 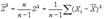называют исправленной выборочной дисперсией.

Очевидно, что 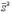- несмещенная и состоятельная оценка для параметра :

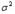Проверим несмещенность:

Замечание: так как при 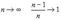, то на практике для оценки 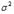применяют (3’) ввиду ее удобства.

В качестве оценок для среднего квадратичного отклонения 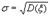берут статистик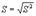и и .Можно показать, что это – состоятельные оценки:

но обе оценки будут смещенными:

Интервальные оценки неизвестных параметров распределения.

1) Интервальная оценка и ее надежность.

Рассмотрим выборку 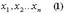. Совокупность независимых случайных величин имеет тот же закон распределения, что и .

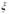Пусть 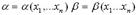статистики такие, что всегда a<в, тогда (a,в)– случайный интервал.

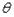– оцениваемый параметр.

Def: если случайный интервал (a,в)может покрывать неизвестный параметр 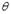, то этот интервал называется интервальной оценкой для параметра .

Пусть вероятность того, что параметр 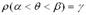, тогда вероятность y называется надежностью или доверительной вероятностью интервальной оценки (a,в).

Естественно, что значения y берут близкими к единице. Обычно y берут 0.95, 0.99, 0.999.

С повышением надежности оценки увеличивается длина доверительного интервала.

2) Доверительный интервал для нормально распределенной случайной величины при известной дисперсии .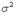

Рассмотрим случайную величину 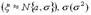– известная величина. Требуется построить доверительный интервал 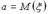. Для решения данной задачи рассмотрим статистику neX– выборочная средняя. Можно показать, что neXтакже подчинена нормальному закону.

Для нормального распределения случайной величины справедливо равенство:

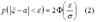
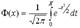– функция Лапласа.

Применим равенство (2) к выборочной средней:

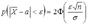
Выберем E так, что бы 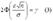заданная надежность оценки.

Из (3) имеем: .

Итак, доверительный интервал для параметра a имеет вид:

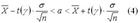
Здесь t(y)выбирается из таблицы значений функций Лапласа: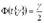

3) Доверительный интервал для генеральной средней при неизвестной дисперсии .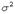

Как и прежде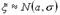

Рассмотрим статистику 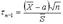. Здесь 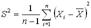– исправленная выборочная дисперсия. Доказано, что статистика 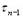имеет закон распределения с плотностью:

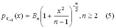
Bn– числа.

Распределение вероятностей, задаваемое плотностью (5) называют “t” – распределением или распределением Стьюдента с (n-1) степенью свободы.

Функция (5) является четной.

При “t” – распределение стремится к нормальному распределению.

Что бы записать доверительный интервал для генеральной средней, рассмотрим равенство:

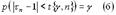
Пользуясь таблицами t” – распределения по заданной надежности и числу степеней свободы (n-1), выбираем t(y,n) из условия (6):

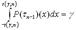
В результате с надежностью y в силу (6) выполняется двойное неравенство:

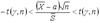
Отсюда выражаем “a”:

Дата добавления: 2014-12-24