Тема 7: Выборочное наблюдение

Выборочное наблюдение – несплошное наблюдение, при котором отбор единиц производится по заранее установленному принципу.

В зависимости от способа организации наблюдения, различают следующие виды выборочного обследования:

- собственно-случайный отбор, который предполагает, что отбор единиц из генеральной совокупности производится случайным образом;

- типический отбор, при котором генеральная совокупность разбивается на группы, после чего в случайном порядке из каждой группы производится отбор единиц;

- механический отбор, при котором отбирается каждый n(N)-ный элемент генеральной совокупности;

- серийный (гнездовой) отбор, при котором отбору подлежат не отдельные единицы совокупности, а серии таких единиц, внутри которых производится сплошное наблюдение.

В зависимости от способа отбора в выборочную совокупность, различаются алгоритмы расчета показателей, характеризующих выборочную совокупность.

Показатели характеристики выборочной совокупности при собственно-случайном бесповторном способе отбора:

- средний размер признака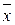

- дисперсия =

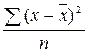
- средняя ошибка выборки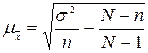

- предельная ошибка выборки 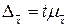где t – коэффициент доверия

t =1 при f(t) = 0,683

t =2 при f(t) = 0,954

t =3 при f(t) = 0,997

- пределы возможных отклонений среднего размера признака в выборочной совокупности от среднего размера признака в генеральной совокупности.

=

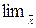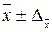
Задание 1: Определить средний процент брака и среднее количество бракованных банок в партии консервов, состоящей из 10 000 банок. Для выборочного наблюдения в случайном порядке было отобрано 900 банок. Анализ качества отобранных банок показал, что средний процент брака в данной совокупности составил 1,5%. Среднее квадратическое отклонение равно 0,3%. Максимальная ошибка выборочного наблюдения с вероятностью 0,997 равна 0,3%.

Решение:

Задание 2: В процессе технического контроля из партии готовой продукции методом случайного бесповторного отбора было проверено 80 изделий, 4 из которых оказались бракованными. Можно ли с вероятностью 0,954 утверждать, что доля бракованных изделий во всей партии не превышает 7%, если процент отбора равен 10?

Решение:

Задание 3: Для определения средних расходов населения района на транспортные услуги проведено 1%-ное обследование, основанное на типическом бесповторном отборе. В городе средние расходы составили 240 руб. на человека в месяц при дисперсии 1849, при этом обследовано 1900 человек; в сельской местности – 90 руб. при дисперсии 1369, обследовано 1100 человек.

На основе исходных данных определить:

1) с вероятностью 0,997 границы средних расходов за месяц на транспортные услуги жителей данного района;

2) сколько городских и сельских жителей района необходимо охватить бесповторным выборочным обследованием для получения данных о среднемесячных расходах с предельной ошибкой, не превышающей 10 руб. при уровне вероятности 0,954.

Решение:

Дата добавления: 2014-12-24