Средние величины и показатели вариации

План:

1. Общие понятия средних величин, их характеристика

2. Средняя арифметическая, простая и взвешенная, ее свойства

3. Структурное среднее (смотри предыдущую лекцию – мода, медиана, квартили и т.д.)

4. Степенные среднее: среднегармоническое, среднеарифметическое, порядок их определения

5. Показатели вариации, среднеквадратическое отклонение, дисперсия

6. Свойства об общих и частных средних

7. Свойства об общих и частных дисперсиях – «золотое правило»

8. Показатели ассиметрии и эксцесса

9. Определение теоретических частот при помощи критерия «хи – квадрат» и выявление соотношения эмпирического распределения к закону нормального распределения.

ОБЩИЕ ПОНЯТИЯ СРЕДНИХ ВЕЛИЧИН, ИХ ХАРАКТЕРИСТИКИ.

Средняя величина – обобщающая характеристика качественно однородной совокупности. Виды:

1. Среднеарифметическое

2. Среднегармоническое

3. Среднегеометрическое

Самое распространенное среднее – средняя арифметическая величина. Бывает:

1. Простая обозначается как «икс» среднее. Равна сумме «икс» делить на «эн». = СУММ х/н. Применяется, когда каждый вариант встречается в совокупности один раз или одинаковое число раз.

2. Взвешенная обозначается как «икс» среднее. Равна сумме «икс» * «эм» и делить на сумму «эм». Применяется, когда каждый вариант встречается в совокупности неодинаковое число раз.

Свойства:

1. Если из вариантов вычесть или прибавить какое-то число (постоянное), то среднеарифметическое уменьшится (увеличится) на это же число. Записывается: (x-c) среднее = x ср. – с

2. Если варианты уменьшить или увеличить в какое-то число раз, то среднеарифметическое уменьшится или увеличится в это же число раз: (х/к) среднее = хср./к

3. Если частоты уменьшить или увеличить в какое-то число раз, то среднее арифметическое не изменится: х_м/ф ср = х_мср.

4. Нулевое: сумма отклонений вариантов от средней равна нулю: СУММ (х-хср.) * м = 0. Доказательство: СУММ (х – хср) * м = СУММ хм – СУММ хм/СУММ м*СУММ м = 0

5. Минимальное: сумма квадрата отклонений вариантов от средней минимальна: СУММ (х – хср)²*м – мин. Или СУММ(х-хср)*м меньше СУММ(х-сонст)²*м при хср не равном сонст. Доказательство: СУММ (х – сонст)²*м, вводим +-хср., СУММ [(х-хср) + (хср-сонст)]²*м = СУММ(х-хср)²*м + 2(хср-сонст)(СУММ х-хср) *м + (хср – сонст)² * СУММ м

ПОКАЗАТЕЛИ ВАРИАЦИИ.

Для характеристики статистической совокупности недостаточно расчета средней величины, так как она не учитывает вариацию внутри распределения. Пример: первая группа сдала на 2-5, а вторая на 3,4 – и там и там среднее арифметическое – 3,5. Не показывается распределение.

Вводится среднеквадратическое отклонения (сигма). Ее характеристика:

1. Является обобщающей характеристикой вариации.

2. Именованная величина, выражается в тех же единицах, что и варианты

3. Коэффициент вариации (V) (в процентах). Если он меньше или равен 40%, то вариация незначительная внутри распределения, а совокупность качественно однородна.

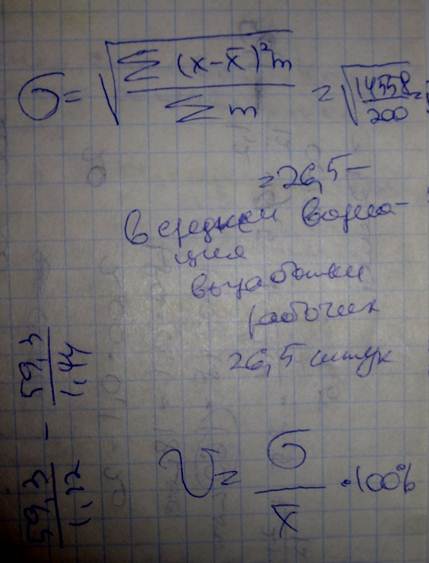
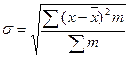
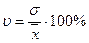
СРЕДНЯЯ ГАРМОНИЧЕСКАЯ И СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ.

На практике не всегда можно применять формулу средней арифметической величины, так как отсутствуют все исходные данные. Например: в розничная торговля ведется стоимостной учет выпущенной продукции и отсутствуют данные о натуральных показателях: штуки, килограммы, метры. Поэтому для расчета средней цены применяется средняя гармоническая величина.

Средняя гармоническая = СУММ М/СУММ (М/х), где М = х*м, а х = М/м: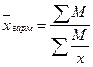

Правило определения формы средней:

1. Если по неявной форме средней дан числитель, то средний определяется по формуле средней гармонической

2. Если по неявной форме средней дан знаменатель, то среднее определяется по формуле средней арифметической

Задача: найти среднюю выработку рабочих по заводу по следующим данным:

Цех	Средняя выработка одного рабочего (шт/чел.) – х	Выпуск продукции, шт. – М	Число рабочих (получаемая величина), чел. = М/х
По двум цехам:	850/50 – 17 штук на человека	СУММ = 850	СУММ М/х = 50

Средняя выработка одного рабочего = выпуск продукции/число рабочих. В данном случае это будет вариантом «икс» - х.

Выпуск продукции – производная величина, обозначается М.

Цех	Средняя выработка одного человека, шт/чел. – х	Число рабочих, чел. – м	Выпуск продукции,шт. – х*м
По двум цехам:	СУММ хм/СУММ м = 850/50 = 17	СУММ м = 50	СУММ хм = 850

Найти среднюю урожайность каждого поля

Поля	Средняя урожайность, ц/га – х	Валовой сбор, ц – М	Площадь поля, га
	1,5
	2,5
По двум полям:	90/44 = 2,045

Обратная задача:

Поля	Средняя урожайность, ц/га – х	Площадь поля, га - м	Валовой сбор, ц
	1,5
	2,5
	90/44 = 2,045

Показатель (3-ий) формы ассиметрии – As =(хсреднее – мода)/ сигму.

· Если показатель положительный – правосторонняя асимметрия

· Если отрицательный – левосторонняя асимметрия

Четвертая формула ассиметрии не показывает направление зависимости, а измеряет степень существенности асимметрии. Формула: модуль As/ сигму по As, где As = Мю₃/ сигма₃, где мю – центральный момент третьего порядка и Мю₃ = СУММ (х – хср)³ * м / СУММ м.

По нашей таблице: 911607,6/200 = 4558,038 – мю³

As = 4558,038/26,5³ = 0,24 – асимметрия.

среднеквадратическая ошибка асимметрии (сигма по As) = Корень из (сигма (н-1)/(н+1)(н+3)) = 0,171 = 1,4 – в нашем случае асимметрия несущественная и ее наличие объясняется влияние случайных обстоятельств.

Теперь по 4-ой формуле: модуль из 0,24/ 0,171. Вывод: если дробь меньше трех, то асимметрия несущественна, ее наличие объясняется влиянием случайных обстоятельств. Если эта дробь больше трех, то асимметрия существенна и распределение признака в генеральной совокупности не является симметричным.

ЭКСЦЕСС.

Показатель, который учитывает высоковершинность или плосковершинность распределения. Обозначается буквой Е = Мю₄ / сигму⁴ – 3, где мю 4-ого порядка = СУММ (х – хср)⁴*м/СУММ м

По нашей таблице: 1447726,648 – мю 4-го порядка Е = 1447726,648/26,5^{4 (493155,063)} – 3 = -0,06. Вывод: если Е положительное, то наблюдается высоковершинное распределение, если отрицательное – плоское или низковершинное.

СВОЙСТВА ОБ ОБЩИХ И ЧАСТНЫХ СРЕДНИХ.

Каждый район – частная совокупность. Среднее общее = СУММ частных средних взвешенных по объемам частных совокупностей. Формула: СУММ x_in_i/СУММ n_i

Расчет общих средних, общих и частных дисперсий (по 8 таблице в учебнике).

№ группы	Средний балл, xi среднее	Число студентов, ni	Xi ср*ni	Сигма итая	Сигма итая^2	Сигма итая^2 * ni	Xср i – xn ср	(Xср i – xn ср)^2	(Xср i – xn ср)^2 *ni
	3,6		86,4	0,1	0,01	0,24	0,24 (-3,36)	0,057	1,368
	3,1		65,1	0,2	0,04	0,84	-0,26	0,0676	1,4196
Итого:			151,5			1,08			2,7876

Правило трех сигм – «золотое правило». Общая дисперсия (сигма в квадрате общая) = средняя из частных дисперсий + межгрупповая дисперсия. Средняя из частных дисперсий показывает, как в среднем изменяются варианты внутри частных групп. Она равна (СУММ частных дисперсий * n_i)/СУММ n_i

По данной таблице: Средняя из частных дисперсий = 1,08/45 = 0,024. Коэффициент вариации = корень из средней из частных дисперсий / 3,36 * 100% = 4,61% - (меньше 40%).

Коэффициент вариации из межгрупповой дисперсии = корень из 0,619/3,36 = 7,404% - (меньше 40%)

Общая дисперсия = 0,024 + 0,0619 = 0,0859. Коэффициент вариации из общей дисперсии = корень из 0,0859/3,36 = 8,72% - незначительная вариация между распределениями и совокупность качественно однородная.

ОПРЕДЕЛЕНИЕ ТЕОРЕТИЧЕСКИХ ЧАСТОТ ДЛЯ ИЗУЧЕНИЯ СООТВЕТСТВИИ ЭМПИРИЧЕСКИХ ЧАСТОТ С ТЕОРЕТИЧЕСКИМИ.

Нормальное распределение характеризуется такими характеристиками: мат. Ожиданием (по статистике, среднее арифметическое) и дисперсия.

Если распределение теоретических частот близко к нормальному распределению (то есть к распределению теоретических частот, то хср. и сигма являются объективными характеристиками данного распределения). Для этого нужно найти теоретические частоты. Пирсен изучил эти вопросы и приравнял теоретическую частоту:

m_t = n*i/сигма * 4(t), где 4(t) – плотность вероятности, а n*i/сигма – константа. В нашем случае= 200*20/26,5 = 150,94 – постоянная величина.

T(стандартное отклонение) = x-x^-/сигму. В нашем случае: 0,0219. У нас 1-е число -2,411, берем в таблице 2,4 и сверху 11 На пересечении 0,0219 (для первой строчки). Так находим по каждому интервалу. Потом каждую полученную величину умножаем на константу 150,94.

17-я колонка: 1-16 (первая минус 16-я). 16-я колонка – это округленная пятнадцатая.

Пирсен сравнивал хи квадрат расчетное с хи квадрат теоретическое. В нашем случае хи квадрат расчетное равно 4,8. Хи квадрат теоретическое – с заданной вероятностью (как правило 0,95 и числом степеней свободы к=n_гр -3, где n_{гр –}число групп (интервалов). В нашем случае к = 5. Значение верхнего альфа хи квадрат в зависимости от вероятности числа степеней свободы. В нашем случае чаще всего встречается 0,95, поэтому в нашем случае, с вероятностью 0,95 и к=5 хи квадрат теоретическое равно 11,1 (по 2-ой таблице). Если хи квадрат расчетное меньше хи квадрат теоретическое (табличное), то гипотеза о близости распределения рабочих по выработке закона нормального распределения не отвергается. А если будет больше, то отвергается. Вывод: дисперсия и мат. ожидание являются объективными характеристиками для данного распределения, если эмпирическое распределение близко к теоретическому, так как mt – нормальное распределение, которое характеризуется средней и среднеквадратическим отклонением.

Дата добавления: 2014-12-24