Правила игры

Предисловие.

Теоретическая кривая распределения– это кривая, выражающаяфункциональную связь между изменением варьирующего признака и изменением частот и характеризующая определенный тип распределения.

Различают следующие виды эмпирических кривых распределения:

1. одновершинные кривые, которые, как правило, характерны для однородных совокупностей:

· симметричные;

· несимметричные: умеренно-ассиметричные, крайне – ассиметричные; V-образные.

2. многовершинные кривые – характеризуют неоднородные совокупности распределения явлений, появление двух и более вершин приводит к необходимости перегруппировки данных с целью выявления более однородных групп.

Симметричным называется распределение, в котором частоты любых двух вариантов, равностоящих в обе стороны от центра распределения, равны между собой. Для симметричных распределений средняя арифметическая, мода и медиана равны между собой.

Несимметричное распределение:

Умеренно-ассиметричное распределение – такой вид распределения, при котором малая часть частот находятся по одну сторону от центра распределения, а большая часть частот находится по другую сторону на одинаковом расстоянии.

В зависимости от того, какая ветвь кривой вытянута – правая или левая, различают правостороннюю положительную или левостороннюю отрицательную асимметрию (рис. 1).

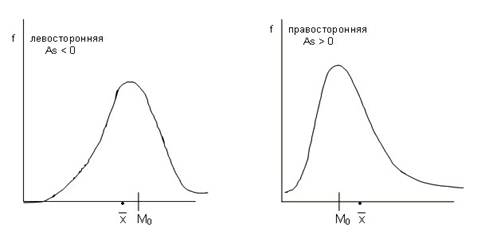
Рисунок 1 – Правосторонняя и левосторонняя асимметрия

Крайне ассиметричными называются ряды распределения, у которых частоты постоянно возрастают или убывают.

При V-образном распределении частоты вначале убывают, а потом возрастают.

В практике статистического исследования встречаются различные виды теоретических распределений распределения: нормальное, логарифмическое, биноминальное, Пуассона и др. Каждое из теоретических распределений имеет специфику и свою область применения в различных отраслях знания.

Нормальное распределение, также известное, как распределение Гаусса, является одним из наиболее известных непрерывных распределений.

В качестве некого стандарта теоретического закона распределения выступает нормальный закон распределения, с которыми сравниваются другие распределения. Распределение признаков совокупности называется нормальным, если этот признак представляет собой результат воздействия множества факторов случайных и независимых или слабозависимых, и влияние каждого из них мало по сравнению с общим воздействием факторов.

Нормальный закон распределения используется для аппроксимации (выравнивания) эмпирических кривых распределения и сопоставления их с теоретическими.

Функция нормального распределения, т. е. простейшее каноническое уравнение нормальной кривой, выглядит следующим образом:

,

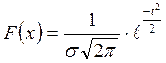где F(x) – ордината кривой нормального распределения (частости);

е=2,7182 – основание натурального логарифма;

p=3,1415 – постоянное число:

Представленная функция является табулированной и может быть определена с помощью математико-статистической таблицы.

Из данной формулы видно, что ординаты (частоты) нормальной кривой являются функцией нормированного отклонения t.

Поэтому необходимо вычислить индивидуальное нормированное отклонение, которое используется для установления вероятности попадания значений признака в заданный интервал.

,

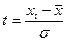где 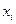– варианты;

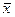– средняя величина;

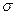– среднее квадратическое отклонение.

Таким образом, кривая распределения будет зависеть от средней величины и среднего квадратического отклонения (рис. 2).

При нормальном распределении вариационный ряд распределения укладывается в границы: 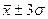(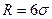) и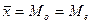

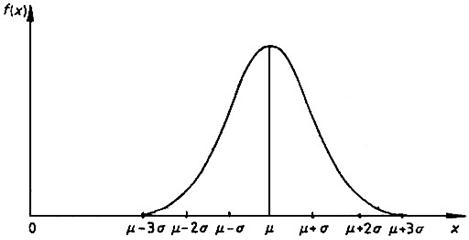
Рисунок 2 – Кривая нормального распределения

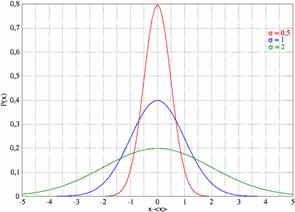
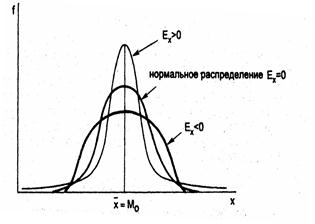
Так как распределение зависит от уровня вариации, т.е. от значений среднеквадратического отклонения, то кривая распределения будет иметь различные вершины. Эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения (рис. 3).

Рисунок 3 – Эксцесс распределения

Логарифмические нормальные распределения играют большую роль в математической статистике, так как встречаются очень часто в практике обработки наблюдений и легко преобразуются к нормальному распределению. Для экспериментатора было бы непростительно провести, например, регрессионный анализ по результатам наблюдений, распределенных логарифмически нормально, без их предварительного преобразования.

В начале ХХ века английским математиком Госсетом, известным под псевдонимом Стьюдент, было установлено, что при небольших объемах выборки несмотря на все условия для проявления закона нормального распределения, имеют место отклонения от последнего, причем тем больше, сем меньше выборка.

Распределение Стьюдента – это теоретическое выборочное распределение. При выборочном распределении понимается распределение частот (частостей или вероятностей) значений какого-либо выборочного показателя. Например, распределение, предоставляющее средние значения х из большого числа выборок одинакового объема, называют выборочным распределением средней. Величина нормированного отклонения вычисляется в этом случае по формуле:

,

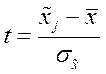где t – критерий Стьюдента;

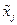– средняя j -й выборки;

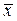– средняя генеральной совокупности;

– среднее квадратическое отклонение выборочной средней от средней величины генеральной совокупности.

Величина , определяемая как средняя ошибка выборки может быть вычилена по формуле:

,

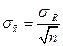где 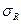– среднее квадратическое отклонение признака х в генеральной совокупности.

Таким образом, значения t во многом зависят от объема выборки. Форма частот также изменяется. Форма распределения Стьюдента похожа на форму нормального распределения. Чем меньше объем выборки, тем более пологой становится форма кривой. При увеличении объема выборки распределение Стьюдента приближается к нормальному. Уже для n=50 расхождения между ними несущественны. Отличием является то, что хвосты распределения Стьюдента медленнее стремятся к нулю, чем хвосты нормального распределения.

t-распределение Стьюдента – это непрерывное одномерное распределение с одним параметром – количеством степеней свободы. С помощью t-распределения устанавливается соотношение между возможным расхождением значений средних в выборке в генеральной совокупности, с одной стороны, и с вероятностью такого события – с другой.

Есть и другие разделы статистики, в которых появляются случайные величины, распределенные по Стьюденту. Например, распределение Стьюдента используется при оценке значимости коэффициента корреляции Пирсона.

Биномиальное распределение B(n,p) – это распределение числа успехов в серии из n экспериментов, каждый из которых завершается успехом с вероятностью p. Важными предельными случаями биномиального распределения являются распределение Пуассона и нормальное распределение.

Если X – биномиальная случайная величина, то

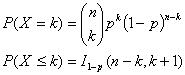
Распределение Пуассона – это дискретное распределение, являющееся одним из важных предельных случаев биномиального распределения.

Если вариационный ряд представляет собой распределение по дискретному признаку, где при увеличении значений признака х частоты начинают резко уменьшаться, а средняя арифметическая, в свою очередь, равна или близка по значению к дисперсии (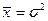), такой ряд выравнивается по кривой Пуассона.

Кривую Пуассона можно выразить отношением:

,

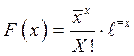где F(x) – вероятность наступления отдельных значений х

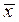– средняя арифметическая ряда.

При выравнивании эмпирических данных теоретические частоты можно определить по формуле

,

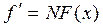где f' – теоретические частоты;

N – общее число единиц ряда.

Сравнивая полученные величины теоретических частот f' c эмпирическими (фактическими) частотами f, убеждаемся, что их расхождения могут быть весьма невелики.

Распределение Пуассона широко используется для аппроксимации биноминального распределения, когда на то есть необходимые условия. Биноминальное распределение является дискретным, варьирующий признак принимает только два значения х₁ и х₂, частоты характеризуют вероятность появления различного числа значений в n испытаниях.

Классическим примером случайной величины, распределенной по Пуассону, является количество машин, проезжающих через какой-либо участок дороги за заданный период времен. Также можно отметить такие примеры, как количество звезд на участке неба заданной величины, количество ошибок в тексте заданной длины, количество телефонных звонков в call-центре или количество обращений к веб-серверу за заданный период времени.

2. Понятия о моментах статистического распределения

Для подробного описания особенностей распределения используют дополнительные характеристики – моменты распределения, предложенные

русским математиком П.Л. Чебышевым и успешно примененные А.А. Марковым для рассмотрения возможностей использования закона нормального распределения при изучении сумм большого, но конечного числа независимых случайных величин.

Моментом распределения называется средняя арифметическая величина тех или иных степеней отклонений индивидуальных значений признака от определенной исходной величины.

Моментом k-го (М_k) порядка называют среднюю отклонений вариантов 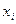от некоторой постоянной величины А в степени k:

,

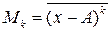
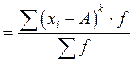где 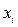– значения признака;

А – постоянная величина, от которой определяются отклонения;

k – степень отклонения (порядок момента).

При исчислении средней в качестве весов могут быть использованы частоты, частости или вероятности. При использовании в качестве весов частот или частостей моменты называются эмпирическими, а при использовании вероятностей – теоретическими.

В зависимости от выбора постоянной величины А различают три вида моментов:

1. начальный момент (М_k) при А=0:

;

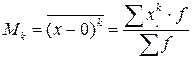2. центральный момент (μ_k) получаются, если за постоянную величину А взять среднюю арифметическую ()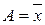

;

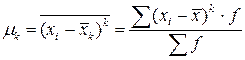3. условный и начальный относительно х₀ момент (m_k), когда А, равная не 0 или 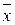, а некоторой производной величине равном х₀ (начало отсчета)

.

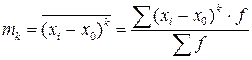Если 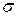принять за стандарт, то отклонение k -го порядка к стандарту 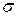в k -й степени будет называться нормированным моментом:

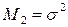
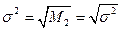
В статистической практике пользуются в основном моментами 1-го, 2-го, 3-го и 4-го порядка, которые представлены в таблице.

Таблица – Основные виды моментов распределения

Порядок (k)	Виды моментов
Начальные А=0	Центральные А=	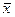Условные А=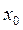
0-й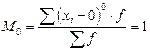
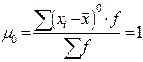
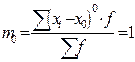
1-й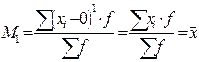
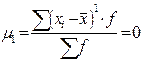
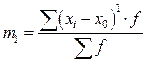
2-й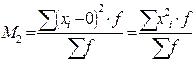
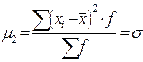
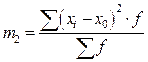
3-й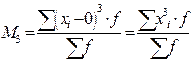
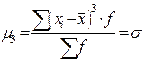
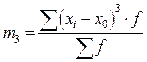
4-й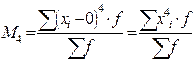

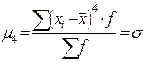
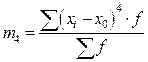
Настоящие правила шахмат (далее по тексту – Правила) разработаны в соответствии с Правилами шахмат ФИДЕ (Международной шахматной федерации), действуют в официальных соревнованиях по шахматам, проводимых общероссийской, региональными и местными спортивными федерациями развивающими вид спорта «шахматы» и иными организациями на всей территории Российской Федерации.

Правила не могут учесть все ситуации, которые могут возникнуть в процессе игры, и не предусматривают решение организационных вопросов. В тех случаях, когда статьи Правил не могут урегулировать ситуацию, решения должны приниматься на основе аналогичных ситуаций, рассматриваемых в Правилах.

Термин «арбитр», используемый в настоящих Правилах, равнозначен термину «спортивный судья по виду спорта «шахматы». Спортивный судья в виде спорта «шахматы» - физическое лицо, уполномоченное организатором спортивного соревнования обеспечить соблюдение правил вида спорта и положения (регламента) о спортивном соревновании, прошедшее специальную подготовку и получившее соответствующую квалификационную категорию.

Правила предполагают, что арбитры обладают необходимой компетенцией, здравым смыслом и абсолютно объективны.

Участники соревнований, арбитры, организаторы, тренеры, иные официальные лица, принимающие участие в указанных соревнованиях, обязаны в своих действиях руководствоваться настоящими Правилами

Правила включают следующие разделы: Правила игры, Правила соревнований (классические шахматы), Правила соревнований по быстрой игре (рапид), Правила соревнований по игре в блиц (молниеносная игра), Алгебраическую нотацию, Правила проведения соревнований (турнирные правила), Правила применения дополнительных показателей.

Дата добавления: 2014-12-24