Теоретико-множественные операции РА

Реляционная алгебра

Манипуляционная часть РМД

Манипуляционная часть может быть реализована на основе двух подходов:

1. основан на РА – процедурный подход;

2. основан на РИ – декларативный подход.

Доказано, что 1 и 2 являются эквивалентными, т. е. Любой набор операций РА может быть представлен в виде высказываний РИ и обратно. Важно, что и 1, и 2 обладают свойством замкнутости. Это – замкнутость по отношению к тем объектам, над которыми происходит манипуляция. Т.е. в результате любых корректных операций из отношений получаются новые реляционные отношения. Т.е. в результате этого из отношений должны получаться только отношения.

Реализация манипуляционной части происходит в любых СУБД на языке данных, а именно на DML. DML должен отображать либо 1, либо 2. на практике трудно выдержать это и реальные реализации содержат часть 1 и часть 2. Примером DML является SQL.

РА основана на наборе операций теории множеств. РИ основано на теории предикатов.

Все операции в РА могут быть разделены на:

1. теоретико-множественные;

2. специальные реляционные.

К 1 относятся операции: объединение, пересечение, разность, прямое произведение. К 2 относятся операции: ограничение, проекция, соединение, деление. Кроме этих двух групп операций для обеспечения замкнутости необходимо ещё две операции: присваивание, переименование.

Объединение двух отношений – отношение, включающее все кортежи, входящие хотя бы в одно из объединяемых отношений.

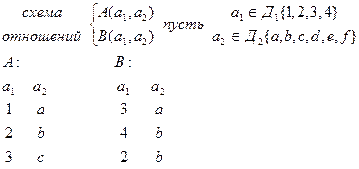
Пересечение двух отношений – отношение, включающее все кортежи, входящие в оба отношения.

Разность двух отношений – отношение, включающее все кортежи, входящие в первое отношение и не входящие во второе.

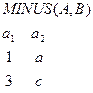
Прямое произведение двух отношений – отношение, кортежи которых являются сцеплением (конкатенацией) кортежей первого и второго отношений.

Пусть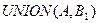

Следовательно, операция выполняется не всегда. Необходимо, чтобы объединяемые отношения были совместимы по объединению, т. е. Объединяемые отношения должны иметь одинаковые схемы. Когда совпадают домены и не совпадают атрибуты – это частичная совместимость. Она может быть доведена до полной, если выполнить операцию переименования. Переименование – операция, в результате которой получают отношение, тело которого совпадает с телом исходного, а атрибуты, т. е. их имена изменены. Т.е. .

В операции прямого произведения:

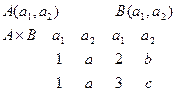
Совместимость по прямому произведению состоит в том, что множество имён атрибутов не должны пересекаться. Любые два отношения могут быть сделаны совместимыми по прямому произведению, если применить операцию переименования.

Дата добавления: 2014-12-25