Методические Указания к решению задач

УКАЗАНИЯ ПО ОФОРМЛЕНИЮ ЗАДАНИЯ

СОДЕРЖАНИЕ И ОБЪЕМ ЗАДАНИЯ

ЦЕЛЬ И ЗАДАЧИ РАБОТЫ

Уфа 2012

УДК 504

ББК 22.15

Н 36

Рекомендовано к изданию методической комиссией механического факультета (протокол №3 от 17 октября 2012 г.)

Составители: доцент Тархова Л.М

ст. преподаватель Урманов В.Г..

Рецензент: доцент Валеев В.Ш..

Ответственный за выпуск: заведующий кафедрой начертательной геометрии и графики доцент Тархова Л.М.

ФГБОУ ВПО «Башкирский ГАУ», кафедра Начертательной геометрии и графики, тираж 50 экз.

ВВЕДЕНИЕ

В методических указаниях приведены рекомендации по решению и оформлению позиционных и метрических задач на эпюре Монжа. Рассмотрена методика построения линии взаимного пересечения кривых поверхностей

1.1 Приобретение умений и навыков:

1.1.1 Выполнения прямоугольного чертежа точки, прямой и плоскости, кривых линий и поверхностей.

1.2 Освоение методики:

1.2.1 Разработки алгоритмов решения позиционных задач.

1.2.2 Разработки алгоритмов решения метрических задач.

1.2.3 Решения обобщенных позиционных задач.

По заданным определителям геометрических фигур построить их эпюр Монжа и решить 7 задач. Варианты определителей геометрических фигур для 7 задач приведены в таблицах приложения А. Задание выдается и принимается согласно графику контроля самостоятельной работы студентов.

При изучении курса, необходимо: прежде всего, ознакомиться с программой, приобрести учебную литературу и тщательно продумать календарный план самостоятельной работы.

При изучении начертательной геометрии следует придерживаться следующих общих правил:

1. Изучение предмета вести последовательно и систематически. Следует избегать механического запоминания теорем, отдельных формулировок и решений задач. Студент должен разобраться в теоретическом материале и уметь применять его к решению конкретных задач.

2. В начальной стадии изучения курса начертательной геометрии полезно прибегать к моделированию изучаемых геометрических форм и их сочетаний. Значительную помощь оказывают зарисовки изображений моделей, а также их простейшие макеты. В дальнейшем надо выполнять всякие операции с геометрическими формами в пространстве на их проекционном изображении, не прибегая уже к помощи моделей и зарисовок.

Контрольная работа представляет собой эпюры (чертежи), которые выполняются по мере последовательности прохождения курса.

Задачи на контрольные работы индивидуальные. Они представлены в вариантах. Студент выполняет тот вариант задания, номер которого соответствует сумме трех последних цифр его шифра. Если, например, учебный шифр 7133, то он во всех задачах выполняет седьмой вариант (1+3+3=7). Для задачи №7 вариант задачи выбирается как сумма двух последних цифр шифра, например для шифра 7133 задаче №7 будет соответствовать шестой вариант (3+3=6)

Контрольная работа представляется на рецензию в полном объеме. Представление ее по частям (отдельные эпюры) не разрешается.

Если работа не зачтена, преподаватель в рецензии указывает какую часть контрольной работы надо переделать или же выполнить всю контрольную работу вновь. На повторную рецензию следует высылать всю контрольную работу полностью.

Эпюры контрольной работы выполняются на листах чертежной бумаги формата А3 по ГОСТ 2.301-68. Все надписи, как и отдельные обозначения, в виде букв и цифр на эпюре должны быть выполнены стандартным шрифтом размером 3,5 или 5 в соответствии с ГОСТ 2.304-81.

Графические построения в каждом чертеже выполнить в избранном масштабе и сначала в карандаше. После проверки и уточнения чертежа обвести его пастой, приняв толщину сплошной линии равной S=0,8-1,0 мм и обязательно сохранить вспомогательные построения, которые при этом должны иметь соответствующие буквенные и цифровые обозначения.

Исходные условия задачи на чертежах желательно выполнить черной пастой, вспомогательные построения и полученные результаты – другими цветами. Все основные вспомогательные построения должны быть сохранены.

Заполнить основную и дополнительные надписи. Таблицу определителя на каждом чертеже, а также условия задачи на поле чертежа заполнить шрифтом №5.

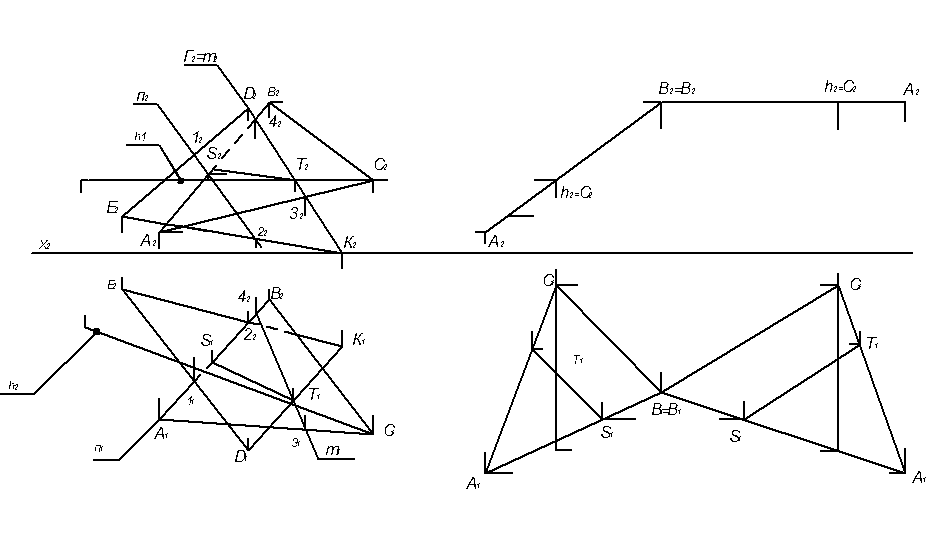
4.1 Задача 1. Построить линию пересечения треугольника АВС и EDK и показать видимость прямых в проекциях. Определить натуральный вид треугольника АВС (рис. 4.1).

Рисунок 4.1 Построение линии пересечения треугольников АВС и EDK  

В левой половине листа формата А3 наносят оси координат и согласно индивидуальному заданию по координатам строят точки А, В, С, E, D, K – координаты вершин треугольников. Линии пересечения треугольников строятся с помощью решения первой основной позиционной задачи (ОПЗ), то есть, используя вспомогательные проецирующие плоскости (посредники) Σ и Г.

На рис. 4.1 показано, что проецирующая плоскость – посредник Г проведена через прямую DK. При этом возникает линия пересечения плоскости Г с плоскостью треугольника – линии m (m_1, m₂). Пересечение линий m₁ и D₁K₁ отмечает проекцию точки пересечения Т₁, которая позволяет найти проекцию Т₂.

Построение второй точки S линии пересечения плоскостей треугольников производится аналогично, т.е. введением плоскости Σ.

Видимость сторон треугольников определяют способом конкурирующих точек. Невидимые отрезки сторон треугольников следует показать штриховыми линиями.

Натуральный вид треугольника АВС определяется плоскопараллельным перемещением, при котором горизонталь h треугольника переводиться в положение, перпендикулярное к плоскости П₂ (h_1┴OX), а сам треугольник переходит в положение фронтально - проецирующей плоскости. Затем вращением вокруг фронтально–проецирующей прямой треугольник проводится в положение, параллельное горизонтальной плоскости проекций. В треугольнике АВС следует показать и линию пересечения его с треугольником EDK.

4.2 Задача 2. Построить линию пересечения поверхностей пирамиды и прямой призмы (рисунок 4.2).

На листе формата А3 согласно индивидуальному заданию наносят координаты точек А,В,С,D вершин пирамиды и координаты точек E,K,G,V вершин нижнего основания призмы, а также высоту h призмы. По этим данным строят проекции многогранников (пирамида и призма). Призма стоит на горизонтальной плоскости проекций, горизонтальные проекции ее вертикальных ребер представляют собой точки, а грани боковой поверхности призмы – отсеки горизонтально – проецирующих плоскостей.

Линия пересечения многогранников строиться по способу ребер, то есть по точкам пересечения ребер каждого из них с гранями другого многогранника. Ребра пирамиды пересекаются с гранями призмы в точках 1,2,4,7. Ребра призмы К и G с гранями пирамиды не пересекаются, а ребра V и DC пересекаются между собой в точке 3. Для построения точек пересечения ребра призмы Е с гранями пирамиды проведена проецирующая плоскость – посредник Σ (Σ1), построены вспомогательные линии m2 и m1, которые позволят отметить точки 6 и 8.

Соединяя каждые пары точек пересечения одних и тех же граней отрезками прямых, получаем замкнутые линии пересечения многогранников, которые принадлежат обеим видимым граням многогранников

Рисунок 4.2 Построение линии пересечения поверхностей пирамиды и призмы

4.3 Задача 3 Построить пирамиду, основанием которой является треугольник АВС, а ребро SA определяет высоту пирамиды (рисунок. 4.3).

На листе формата А3 согласно индивидуальному заданию строят по координатам проекции треугольника. В плоскости АВС построены вспомогательные прямые h и f. В точке А восстановлен перпендикуляр n (n₁, n₂) к плоскости треугольника по правилу n₁┴h₁ и n₂┴f₂. На прямой n отложен произвольный отрезок А–3, который вращением приведен в положение горизонтали, на горизонтальной проекции которой отмечена заданная высота пирамиды Δ (А₁-S^*₁). Возвращая точку S^* в точку S₁, отметим и проекцию S₂ искомой точки S. Затем построены ребра пирамиды SА, SВ, SС. При этом способом конкурирующих точек определяется видимость ребер на проекциях чертежа. Невидимые ребра следует показать штриховыми линиями.

4.4 Задача 4 Построить сечение поверхности заданной пирамиды плоскостью общего положения (рисунок 4.4).

На листе формата А3 согласно индивидуальному заданию выполнить эпюр пирамиды и плоскости. Размеры наносить не обязательно.

Задача может быть решена с помощью способа ребер, при котором определяются точки пересечения всех ребер пирамиды с заданной плоскостью P. Точки 3 и 4 пересечения ребер АВ и АС находятся непосредственно на плоскости П₁. Ребро ВС с плоскостью Р не пересекается. Точки пересечения трех ребер SA, SВ и SС могут быть найдены по методике решения первой ОПЗ, то есть построением трех проецирующих плоскостей, проходящих через эти ребра.

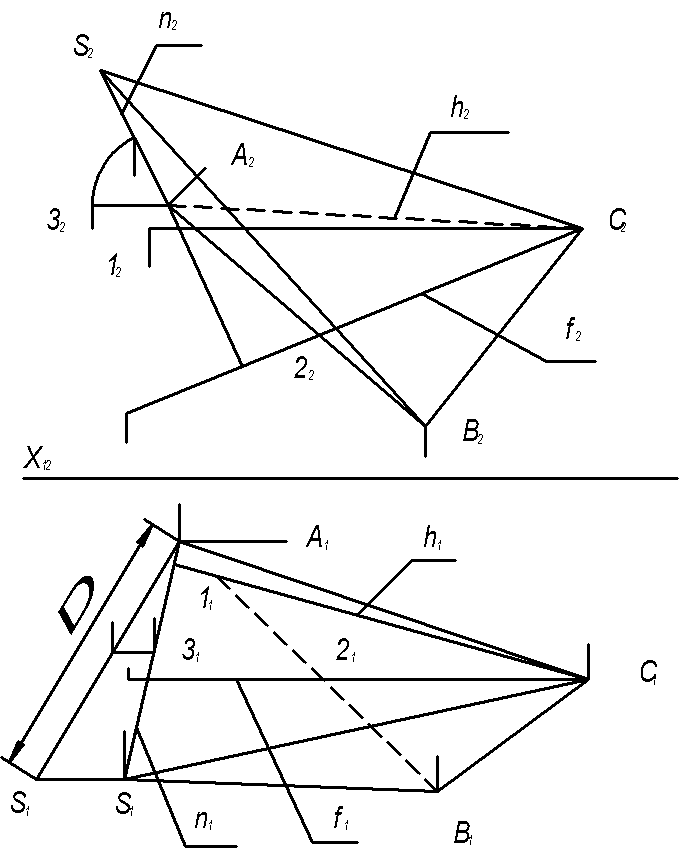
Рисунок 4.3 Построение пирамиды, основанием которой является треугольник АВС, а ребро SA определяет высоту пирамиды.

Задача может быть решена также способом замены плоскостей проекций, когда заданная плоскостью становится проецирующей (рисунок. 4.4). При этом линия пересечения проецируется на дополнительную плоскость в виде отрезка прямой, по которой затем строятся основные её проекции 1₁-2₁-4₁-3₁-1₁ и 1₂-2₂-4₂-3₂-1₂.

4.5 Задача 5 Построить сечение конической поверхности плоскостью общего положения (рисунок 4.5).

По заданным координатам построить проекции геометрических фигур на эпюре. В целях упрощения построения линии сечения введена новая плоскость П₄, перпендикулярная к прямой АВ, которая является горизонталью заданной плоскости АВС. На плоскость П₄ плоскость АВС проецируется в виде прямой, а отрезок 1₄-2₄ представляет собой проекцию диаметра линии сечения (эллипса) заданной плоскостью. На этой линии отмечены проекции центра эллипса О₄, а также точки 3₄ и 4₄ – концы диаметра, перпендикулярного диаметру 1₄-2₄. На основании данных чертежа П₄ на плоскости П₁ построены проекции сопряженных диаметров эллипса 1₁-2₁ и 3₁-4₁, а затем построены фронтальные проекции этих диаметров, то есть – 1₂-2₂ и 3₂-4₂. Затем следует построить приближенную развертку конуса с нанесением на ней линии сечения

Рисунок 4.4 Построение сечения поверхности заданной пирамиды плоскостью общего положения

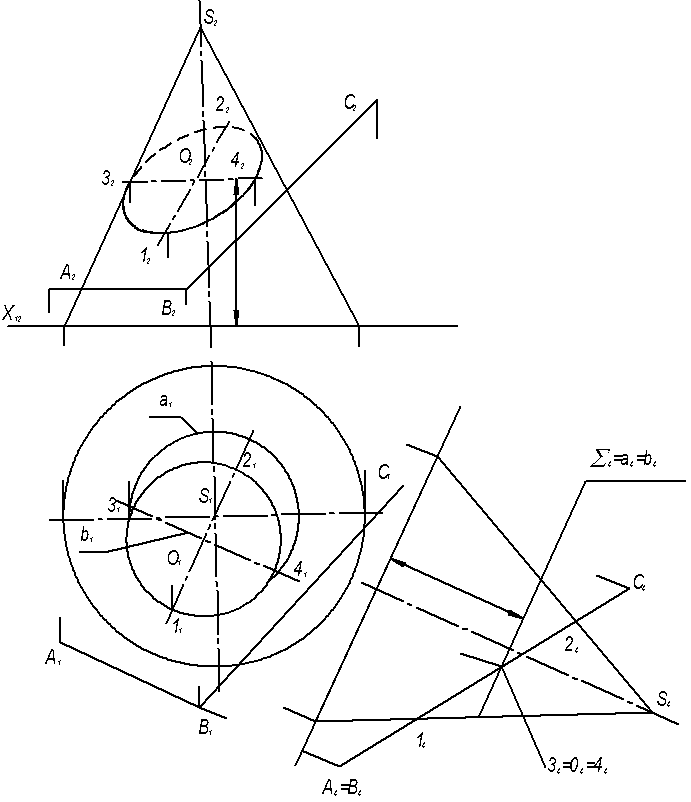
Рисунок 4.5 Построение сечения конической поверхности плоскостью общего положения.

4.6 Задача 6. Построить точки пересечения прямой d с конической плоскостью (рисунок. 4.6).

На формате А3 согласно индивидуальному заданию выполнить эпюр.

Задача решается на основе алгоритма первой ОПЗ. Вспомогательная плоскость Σ при этом проводится через заданную прямую и вершину конуса S. При этом на прямой d отмечена точка А. Затем через вершину S и точку A проведена линия m (m₂; m₁).

Прямые d и m задают плоскость – посредник Σ, которая дает сечение поверхности конуса по образующим – прямым линиям. Пересечение этих прямых с прямой d позволяет отметить искомые точки. Для их построения находим горизонтальные следы прямых d и m – М¹(М¹₁, М¹₂) и N²(N²₁, N²₂ ), а затем след плоскости Σ₁. Пересечение следа Σ₁ с проекцией окружности основания конуса дает точки 1₁ и 2 ₁, а затем горизонтальные проекции прямых сечения – 1₁-S ₁ и 2₁-S₁. Пересечение этих прямых с проекцией d₁ позволяет отметить горизонтальные проекции искомых точек К₁ и L₁, а потом и фронтальные проекции точек К₂ и L₂.

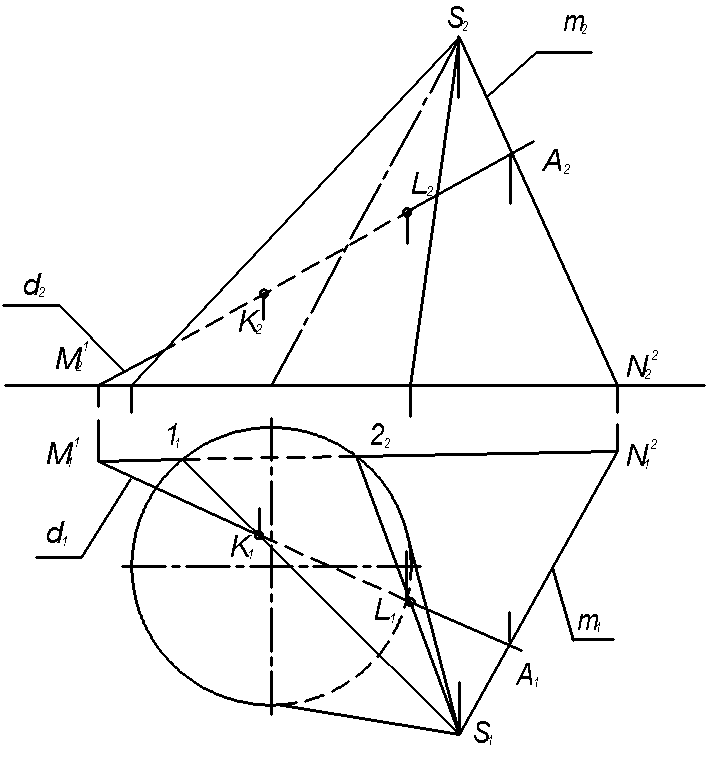
Рисунок 4.6 Построение точек пересечения прямой d с конической поверхностью

4.7 Задача 7. Построить линию взаимного пересечения двух заданных поверхностей (рисунок. 4.7).

Перед решением этой задачи следует изучить вопросы:

- определитель поверхности;

- способы задания и построение поверхностей на чертеже;

- способы построения линий пересечения поверхностей (способ посредников).

- При выполнении графических построений:

- изучить заданные определители двух поверхностей и их геометрическую часть нанести на чертеже;

- завершить чертеж в двух проекциях с нанесением линий каркаса, линий очерка и обрыва;

- выполнить анализ взаимного положения заданных фигур и сделать упрощающие преобразования;

- выполнить анализ ожидаемой линии пересечения, дать ее характеристики;

- наметить количество и расположение опорных точек линии пересечения;

- уточнить и реализовать намеченный алгоритм решения задачи с помощью посредников;

- соединить полученные проекции точек линии пересечения на их проекциях с учетом видимости на чертеже.

На эпюре (рисунок. 4.7) заданы две поверхности второго порядка; проецирующий цилиндр, перпендикулярный П ₂ и четверть поверхности

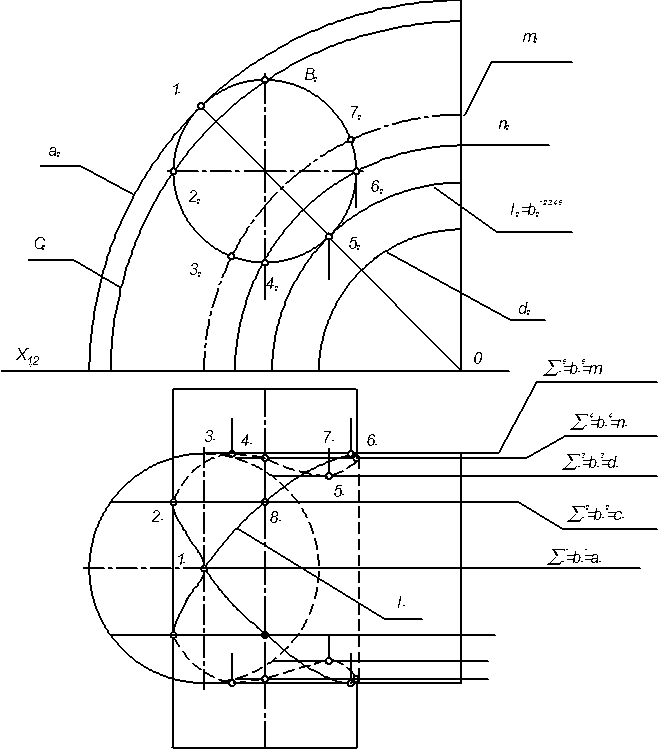
Рисунок 4.7 Построение линии взаимного пересечения двух заданных поверхностей.

открытого тора, который стоит на плоскости П₁. Следовательно, линия их взаимного пересечения представляет собой пространственную кривую четвертого порядка. Фронтальная проекция линии пересечения 1 известна: она представляет собой окружность 1₂. Горизонтальные проекции точек 1₁, 2₁, 3₁, 4₁, 5₁, 6₁, 7 ₁ проекции 1₁ строятся с помощью плоскостей (посредников) Σ¹, Σ², Σ³, Σ⁴, Σ⁵, параллельных плоскости П₂. Посредники рассекают поверхность цилиндра по окружности b^1,2,3,4,5, а поверхность тора – по дугам окружностей a, c, d, n, m. Пересечения b^{1,2,3,4 ,5} с указанными дугами позволяют отметить проекции искомых точек сначала на П₂, а затем на П ₁, чтобы построить 1 ₁

Дата добавления: 2014-12-25