Круговой проводник с током

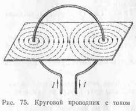Возьмем проводник, согнутый по кругу в виде витка, и пропустим по нему ток (рис. 75). Из чертежа видно, что магнитные линии замыкаются вокруг проводника с током и имеют форму ок­ружностей. Магнитные линии с одной стороны входят в плоскость кругового проводника, с другой — выходят.

Направление поля круго­вого тока можно определить, пользуясь «правилом бурав­чика»

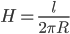Буравчик нужно расположить по оси кругового тока перпендикулярно его плоскости. Если теперь вращать ручку буравчика по направлению тока в контуре, то поступательное движение буравчика покажет направление магнит­ного поля. Напряженность магнитного поля в центре витка с током определяется по формуле:

Закон Био-Савара-Лапласа (формулировка). Расчет напряженности магнитного поля прямолинейного проводника с током.

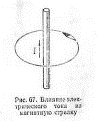
При прохождении постоянного тока по замкнутому контуру, находящемуся в вакууме, для точки, отстоящей на расстоянии 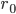, от контура магнитная индукция будет иметь вид:

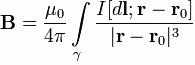
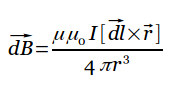Если к прямолинейному проводнику с током поднести магнитную стрелку, то она будет стремиться стать перпендикулярно плоскости, проходящей через ось проводника и центр вращения стрелки (рис. 67).

Это указывает на то, что на стрелку действуют особые силы, которые называются магнитными. Иными словами, если по проводнику проходит электрический ток, то вокруг проводника возникает магнитное поле.

Магнитное поле можно рассматривать как особое состояние пространства, окружающего проводники с током.

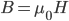
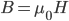При расчетах магнитных полей пользуются величиной, называемой напряженностью магнитного поля (обозначается Н). Магнитная индукция В и напряженность магнитного поля Н связаны соотношением:

Единица измерения напряженности магнитного поля 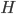ампер на метр (А/м).

Напряженность магнитного поля в однородной среде, так же как и магнитная индукция, зависит от величины тока, числа и формы проводников, по которым проходит ток. Но в отличие от магнитной индукции напряженность магнитного поля не учитывает влияния магнитных свойств среды.

Закон Био-Савара-Лапласа (формулировка). Расчет напряженности магнитного поля на оси соленоида.

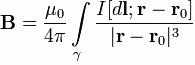
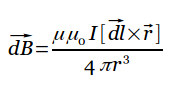При прохождении постоянного тока по замкнутому контуру, находящемуся в вакууме, для точки, отстоящей на расстоянии 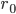, от контура магнитная индукция будет иметь вид:--------------------------------------------------------------------à

Соленоид – катушка индуктивности, выполненная в виде намотанного на цилиндрический каркас изолированного проводника, по которому течет электрический ток. Соленоид представляет собой систему круговых токов одинакового радиуса, имеющих общую ось в соответствии с рисунком 3.2-а.

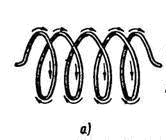
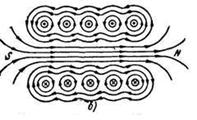ß--Соленоид и его магнитное поле

Если мысленно разрезать витки соленоида поперек, обозначить направление тока в них, как было указано выше, и определить направление магнитных индукционных линий по «правилу буравчика», то магнитное поле всего соленоида будет иметь такой вид, как показано на рисунке.

На оси бесконечно длинного соленоида, на каждой единице длины которого намотано n₀ витков, напряженность поля определяется формулой: H = In₀

В том месте, где магнитные линии входят в соленоид, образуется южный полюс, где они выходят – северный полюс.

Для определения полюсов соленоида пользуются «правилом буравчика», применяя его следующим образом: если расположить буравчик вдоль оси соленоида и вращать его по направлению тока в витках соленоида, то поступательное движение буравчика покажет направление магнитного поля в соответствии с рисунком 3.3.

ßПрименение правила буравчика

Закон полного тока (формулировка). Расчет поля тороида.

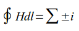Закон полного тока - линейный интеграл вектора напряженности магнитного поля, взятый по замкнутому контуру, равен полному (суммарному) электрическому току, проходящему через поверхность, ограниченную этим контуром или магнитодвижущей силе вдоль замкнутого контура равна полному току, охватываемому этим током.

Магнитное поле тороида — кольцевой катушки, у которой витки намотаны на сердечник, который имеет форму тора (рис. 2). Магнитное поле, как известно из опыта, сосредоточено внутри тороида, а вне его поле равно нулю.

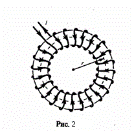В данном случае линии магнитной индукции, как следует из соображений симметрии, есть окружности, у которых центры расположены по оси тороида. В качестве контура возьмем одну такую окружность радиуса r. Тогда, используя теорему о циркуляции, 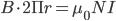, откуда следует, что магнитная индукция внутри тороида (в вакууме):

,

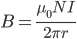где N — число витков тороида.

Если контур проходит вне тороида, то токов он не охватывает и B•2πr = 0. Следовательно, что поле вне тороида отсутствует (что показывает и опыт).

Закон полного тока (формулировка). Расчет магнитного поля массивного проводника конечного радиуса с током.

Линейный интеграл по замкнутому контуру l от напряженности магнитного поля равен полному току, протекающему сквозь сечение, ограниченное этим контуром.

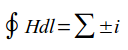
Н – напряженность магнитного поля в данной точке пространства;

dL – элемент длины замкнутого контура L;

α – угол между направлениями векторов H и dL; 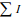– алгебраическая сумма токов, пронизывающих контур L.

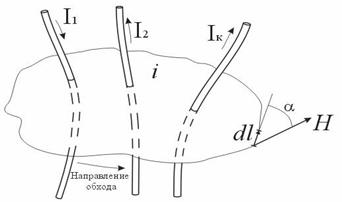Закон полного тока

Ток Iк, пронизывающий контур L считается положительным, если принятое направление обхода контура и направление этого тока связаны правилом правоходового винта (буравчика).

Токи Фуко (вихревые токи) — замкнутые электрические токи в массивном проводнике, возникающие при изменении пронизывающего его магнитного потока. Они являются индукционными токами, они образуются в проводящем теле либо вследствие изменения во времени магнитного поля, в котором оно находится, либо в результате движения тела в магнитном поле, приводящего к изменению магнитного потока через тело или любую его часть. Согласно правилу Ленца, магнитное поле токов Фуко направлено так, чтобы противодействовать изменению магнитного потока, индуцирующему эти токи.

Дата добавления: 2014-12-25