Введение. Изучение затухающих электромагнитных колебаний

Изучение затухающих электромагнитных колебаний

Лабораторная работа № 13

Цели работы: наблюдение затухающих электромагнитных колебаний в контуре с помощью осциллографа; определение характеристик процесса затухания и добротности колебательного контура.

Приборы и принадлежности: катушка индуктивности (L = 0,18 мГн), конденсатор (C = 1,0 мкФ), магазин сопротивлений Р-33, генератор импульсов, выпрямитель ВУП-2М, осциллограф типа С1-73, ключ.

Литература: [1], § 11.1; [2], § 51; [3], § 11.2; [4], § 238; [5], § 90; [6], § 174; [7], § 143, 146.

Электрический колебательный контур это цепь, состоящая из включенных последовательно катушки индуктивностью L, конденсатора емкостью C, и резистора сопротивлением R.

Рассмотрим идеализированный контур, сопротивление которого R =0.

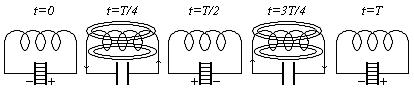
а) б) в) г) д)

Рис. 1

Для возбуждения в контуре колебаний конденсатор предварительно заряжают, сообщая его обкладкам заряд ± q. Если к заряженному конденсатору подключить катушку индуктивности, то в системе возникнут колебания, период T которых зависит от L и C. Рассмотрим последовательные стадии этого процесса. В начальный момент времени t = 0 (рис. 1, а) между обкладками конденсатора имеется электрическое поле, энергия которого равна 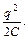При подключении катушки конденсатор начнет разряжаться, и в контуре потечет возрастающий со временем ток I. (ЭДС самоиндукции, возникающая в катушке на этой стадии процесса, препятствует нарастанию тока и предотвращает мгновенную разрядку конденсатора). В результате энергия электрического поля будет уменьшаться, а энергия магнитного поля, равная - возрастать. При R =0 теплота в контуре не выделяется. Следовательно, полная энергия колебательного контура с течением времени не изменяется:

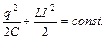(1)

Поэтому в момент времени t = T /4 (рис. 1, б), когда конденсатор полностью разрядится, энергия электрического поля обращается в нуль, а энергия магнитного поля (а следовательно, и ток) достигает наибольшего значения. Начиная с этого момента, ток в контуре будет убывать, а в катушке индуцируется ток, который (согласно правилу Ленца) течет в том же направлении, что и ток разрядки конденсатора. Конденсатор начнет перезаряжаться; в нем возникнет возрастающее со временем электрическое поле, имеющее направление, противоположное тому, которое было при t = 0. Возникшие на обкладках конденсатора электрические заряды препятствуют протеканию тока, который в конце концов обратится в нуль, а заряд на конденсаторе достигнет максимума (рис. 1, в). Далее те же процессы начнут протекать в обратном направлении, и система к моменту t=T придет в первоначальное состояние. Если бы потерь энергии не было, то в контуре совершались бы периодические незатухающие колебания, т.е. периодически изменялись бы напряжение U (и заряд q) на обкладках конденсатора и сила тока I, текущего через катушку индуктивности. При этом происходило бы взаимное превращение энергий электрического и магнитного полей.

Теория дает, что период рассматриваемых (собственных) колебаний в контуре определяется выражением

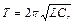(2)

которое носит название формулы Томсона. При этом циклическая частота собственных колебаний

(3)

В любом реальном электрическом контуре происходит преобразование энергий электрического и магнитного полей в тепловую энергию, а также в энергию электромагнитных волн, излучаемых контуром в окружающее пространство. В результате колебания в реальном контуре с течением времени затухают.

Теоретический анализ затухающих колебаний в электрическом контуре приводит к следующим результатам. Зависимость напряжения на обкладках конденсатора от времени описывается выражением

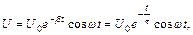(4)

где U ₀ – напряжение на конденсаторе в начальный момент времени (t =0), β = R /2 L – коэффициент затухания, а параметр называется временем релаксации колебаний. При этом частота затухающих колебаний

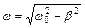(5)

тем меньше собственной частоты ω ₀ колебательного контура, чем больше коэффициент затухания β. Если, как это часто бывает, «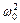, то ω=ω ₀.

Выражение

(6)

можно рассматривать как амплитуду напряжения на конденсаторе, которая убывает со временем по экспоненциальному закону. За время t = τ амплитуда напряжения убывает в е раз. Следовательно, время релаксации это интервал времени, за который амплитуда колебаний уменьшается в е раз.

Прологарифмируем выражение (6):

(7)

Таким образом, натуральный логарифм амплитуды затухающих колебаний является линейной функцией времени.

Затухающие колебания принято характеризовать еще одной величиной, называемой логарифмическим декрементом затухания. Если U_m (t) и U_m (t+T) амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то логарифмический декремент затухания δ определяется выражением

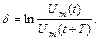(8)

Принимая во внимание (4), получим, что

(9)

Здесь N_e имеет смысл числа колебаний, совершаемых в контуре за время релаксации.

Добротность Q колебательной системы определяется отношением энергии W (t), которой обладает колебательная система в момент времени t, к энергии Δ W, теряемой за период:

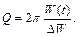(10)

Можно показать (см., [1-7]), что при выполнении условия «

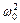
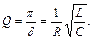(11)

В заключение отметим, что согласно (5) при увеличении коэффициента затухания период затухающих колебаний растет, и при β=ω ₀, иначе при выполнении условия

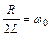(12)

обращается в бесконечность, т.е. движение перестает быть периодическим. В таком случае колеблющаяся величина асимптотически приближается к нулю, когда t Процесс не будет колебательным. Он называется апериодическим.

Дата добавления: 2014-12-25