Исходные данные

Дана эмпирическая выборка случайной величины Х с соответствующими частотами

х	х1	х2	х3	х4
m	m1	m2	m3	m4

. Варианты х, х…., являются равностоящими с постоянным шагом h=x, x….-x. Исходя из свойств задачи, выберем уровень значимости (пусть = 0.05).

Критерий для характеристики степени расхождения между эмпирическими и теоретическими частотами (критерий Пирсона) имеет вид:

. (4.1)

m и z соответственно эмпирические и теоретические частоты.

4.2. Проверка гипотезы о нормальном распределении

генеральной совокупности.

Функция распределения имеет вид: , (4.2)

Характеристиками данного распределения являются математическое ожидание с среднее квадратичное отклонение 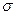∙ (Sl=2).

1.Вычислим их выборочные характеристики:

– выборочное среднее.

- выборочное среднее квадратичное отклонение.

2.Нормировка значений x₁,x₂,…,x_k по формуле .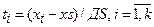

3.Вычисление вероятностей теоретического закона распределения по формуле (4.2)

4.Составление суммы для вычисления x² по формуле (4.1)

.

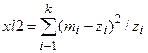5. Выбор из таблицы критерия Пирсона для заданного и k величину 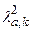(в алгоритме как входное значение обозначим XlT), k=k-Sl-1, где k - число значений случайной величины, Sl - число параметров данного распределения (для нормального – 2).

6. Сравнение xl2 и xlT.

а) если xlT ≤ X12, то вывод сообщения «Данная выборка не соответствует закону нормального распределения».

в) если xlT ≥ Xl2, то вывод сообщения №Данная выборка не соответствует закону нормального распределения».

7.Вывод массивов t_i и z_i, 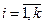. Конец задачи.

Методический пример 1.

Эмпирическое распределение имеет вид:

хi	5	7	9	11	13	15	17	19	21
mi	15	26	25	30	26	21	24	20	13

k=9 - число вариант: 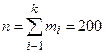– объем выборки; h=x_i…k –x_i =2; = 0.05 - уровень значимости.

Вычислим:

1. Выборочную среднюю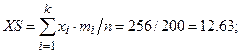

2. Выборочную дисперсию и среднее квадратичное отклонение

Нормировка значений x₁,x₂,…x_k по формуле t_i = (x_i -xs)/ДS и вычисление

.

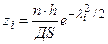xi	5	7	9	11	13	15	17	19	21
ti	-1.62	-1.2	-0.77	0.35	0.08	0.51	0.93	1.36	1.78
zi	9.1	16.5	25.3	32	33.9	29.8	22	13.5	7
(mi – zi)^2 zi	3.8	3.6	0.0	0.1	1.9	2.3	0.2	3.0	5.1

k = k-sl – 1= 9-2-1 = 6. Из таблицы распределения (пр.2) λ² имеем 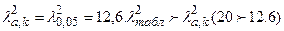гипотеза H₀ не верна.

4.3. Проверка гипотезы для показательного закона распределения.

Функция распределения имеет вид: f(x)=λ∙e^λ∙x (3) x>0

Один параметр распределения λ. Его оценка связана с оценкой среднего значения следующим соотношением λ = 1/XS, (Sl=1).

1. Найдем среднее по формуле и вычислим L=1/XS.

Определим шаг h = x_i+1 – x_i.

2. Вычислим теоретические частоты z_i = n ∙ L∙e^-L∙x.

3.Составим сумму для вычисления λ² по формуле (1).

4. Для заданных (уровень значимости) и k =k-Sl-1 из таблицы Пирсона выберем .

5. Проверка гипотезы H₀.

а) если xlT ≥ Xl2, то вывод сообщения «Данная выборка соответствует показательному закону распределения»;

б) если xlT ≤ Xl2, то вывод сообщения «Гипотеза H₀ не верна, выборка не принадлежит показательному закону».

6. Вывод массива z_i, 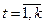, конец задачи.

Методический пример 2.

Эмпирическое распределение имеет вид:

xi	1	3	5	7	9
mi	20	15	11	9	5

Пусть - число вариант, n =∑m_i = 60

Алгоритм расчета .

1. Вычислим выборочную среднюю

XS =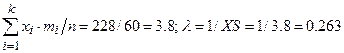

Функция распределения имеет вид:

F(x) = λ∙e^{-λ x} =0.263∙e^{-0,263 x}

Построим график на EUREKA.

Вычислим теоретические частоты по формуле

x_i=n∙h∙f(x_i)=60 ∙2 ∙0.263∙e^{-0,263 x}

Составим таблицу

xi	1	3	5	7	9
mi	20	15	11	9	5
zi	24.3	14.3	8.5	5.1	3
mi-zi	-4.3	0.7	2.5	3.9	2.0
(mi-zi)^2 zi	0.764	0.33	0.342	2.98	1.33

Из таблицы критерия λ ¹ выберем 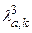. Данное распределение имеет один параметр λ (Sl=1). Тогда k=k – S1-l=3; .

Вывод: не оснований отвергнуть гипотезу о распределении Х по показательному закону.

Примечание: Для интервального вариационного ряда

xi-хi+1	x1-x2	x2-x3	…	xi-хi+1
mi	m1	m2	…	mi

Вычисление выборочных средних и дисперсий производится путем вычисления среднего каждого интервала по формуле:

h_i =(x_i+1 – x_i)/2; XS = ∑ h_i ∙m_i/∑ m_i.

Вероятность для каждого интервала вычисляется по формуле

, где

- функция Лапласа.

Теоретические частоты имеют вид z_i = n ∙ P_i. Остальные пункты алгоритма сохраняются без изменения.

Показательное распределение

б) Дано интервальное эмпирическое распределение.

Методический пример 3.

xi –xi+1	0-5	5-10	10-15	15-20	20-25	25-30
mi	1.33	45	15	4	2	1

Требуется при уровне значимости =0.05 проверить гипотезу о том, что вариационный интервальный ряд распределен по показательному закону. Для каждого интервала найдем среднее t_i =(x_i+1 – x_i)/2, 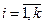, k – число интервалов (k=6). Среднее для всего ряда определяется по формуле . Найдем оценку параметра λ =1/XS-0.2.

Таким образом, дифференциальная функция предполагаемого показательного распределения имеет вид f(x) = 0.2∙e^-0.2∙x , (x>0).

Найдем вероятности показания х в каждый из интервалов по формуле

P_i = P(x_i < x < x_i+1) = e^-λ∙x_i+1

Например, для первого интервала

P_i = P(0 < x <5) =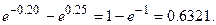

Аналогично определяются и остальные Р₂, Р₃,…

Теоретически частоты определяются по формуле z_i= n∙P_i = .

4.4. Индивидуальные задания

1.Проверка гипотезы о нормальном распределении.

Для нечетных вариантов

x1	1	3	5	7	9	11	13	15	17	19
mi	2	4	4	8	9	b	6	c	4	3

Таблица 5

№ вар.		a	b	c	№ вар.		a	b	c
1	0.01	5	6	2	13	0.05	3	4	3
2	0.025	3	1	6	14	0.95	4	3	6
3	0.05	7	2	3	15	0.975	3	5	2
4	0,95	5	3	1	16	0.01	5	6	3
5	0.975	4	8	3	17	0.025	6	3	2
6	0.01	6	2	1	18	0.05	4	5	2
7	0.025	5	5	1	19	0.95	7	2	3
8	0.05	6	3	8	20	0.975	6	4	2
9	0.95	4	6	3	21	0.01	5	3	6
10	0.975	4	3	2	22	0.025	4	5	6
11	0.01	6	7	2	23	0.05	7	3	6
12	0.025	4	4	3	24	0.95	8	4	5

2. Проверка гипотезы о показательном распределении

а) для нечетных вариантов

xi	1	2	3	4	5	6	7	8	9
mi	15	13	a	10	a	9	c	4	4

б) для четных вариантов

xi	2	3	4	5	6	7	8	9	10
mi	10	8	В	7	с	6	а	3	2

Примечание: Значение , a,b,c по вариантам выбрать из таблицы 1.

4.5. Порядок выполнения лабораторной работы.

1. Выбрать входные данные по варианту.

2. Составить блок-схему, программу и выполнить расчеты на ЭВМ.

3. По теоретическим z_i и эмпирическим x_i частотам построить полигон на одном чертеже, анализ результатов.

4.6. Контрольные вопросы.

1. Постановка задачи проверки статистической гипотезы о законах распределения. Формула для вычисления λ².

2. Порядок построения теоретических частот.

3. Проверка гипотезы H₀ путем сопоставления λ² и 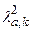и пояснить результаты на ЭВМ.

5. Математический анализ случайных процессов.

(Лабораторная работа № 5)

5.1 Постановка задачи и алгоритм расчета.

Случайная функция времени характеризует процесс изменения случайной величины с течением времени. Поэтому случайные функции времени обычно называют случайными процессами.

Эксперимент проводится во времени. Если проведено n -независимых опытов, то в результате получим n -реализаций (x₁(t), x₂(t),...x_n(t). Каждая реализация есть обычная (неслучайная) функция. Для каждого дискретного значения времени известны значения всех реализаций (x₁(t_j), x₂(t_j),...x_n(t_j), j = 0,1,2…,m. Последовательность построения алгоритма показана на следующем примере.

№№ п/п	время реализация	0	1	2	3
x(0)	x(1)	x(2)	x(3)
1	x1(t)	4	5	7	8
2	X2(t)	6	3	4	3
3	X3(t)	5	8	7	6

Количество отрезков времени m = 4; количество реализаций n = 3; шаг n = t_i+1 - t_i = 1. Исходные матрица x(n,m) = x(3,4).

1. Построить графики для реализаций.

2. Определение оценок математических ожиданий для каждого t_j.

.

3. Зависимость Xl(t) показать на графике. С помощью метода наименьших квадратов на ЕUREKA построить приближающий полином.

4. Нахождение оценок корреляционных моментов по формуле

, , .

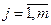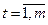Выход матрицы k(m,m):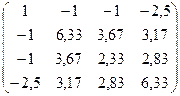

5. Элементы главной диагонали матрицы k являются дисперсиями по отрезкам времени (обозначим S): S_j=k_n, .

S=(1;6.33;2.33;6.23. Среднеквадратичные отклонения имеют вид

(обозначим Sl):

6. Составление матрицы нормированных коэффициентов корреляции по формуле

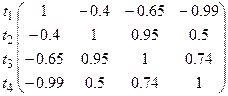
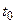
Аргументами являются отрезки (пары) времени t_j и t_i: при j=1 имеем одно время и поэтому R₂=0; Абсолютные значения и знаки элементов характеризуют тесноту связи реализаций в различные моменты времени.

7. Для характеристики степени разбросанности реализаций случайной функции вокруг оценки вычислить: .

На графике Xl(t) показать интервалы Y_t Yl_t

t	0	1	2	3
Yi	4.33	2.33	4.14	3.19
X1i	5	5.3	6	5.7
Y1i	6.03	7.82	7.15	8.18

8. Расчет характеристик стационарных случайных процессов. Как правило, математическое ожидание такой случайной функции постоянно и не зависит от значения аргумента t_j.

Вычислим среднюю математического ожидания: ;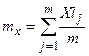

Оценки дисперсии: .

Имеем: m_x = 5.42, DX = 4, SX = 2.

9. Вычисление нормированной корреляционной функции rx (для случайной стационарной функции она зависит только от разности аргументов

). Элементы rx_j вычислим из матрицы R:

r₁ = (R₁₁+R₂₂+R₃₃+R₄₄)/4=(1+1+1+1)/4=1 (главная диагональ)

r₂ = (R₁₂+R₂₃+R₃₄)/3=(-0.4.+0.95+0.74)/=0.92

r₃ = (R₁₃+R₂₄)/2=(-0.65+0.5)/2=-0.15

r₄ = R₁₄/1= -0.99

Составим зависимость, построим график

t	0	1	2	3
rxt	1	0.92	-0.15	-0.99

На EUREKA найти модель полученной зависимости (метод наименьших квадратов); Z(h) = e^a∙h ∙cos(b∙h), для данной модели найти a и b и построить график.

5.2. Порядоквыполнения лабораторной работы.

1. Подготовить входные данные в соответствии с вариантом.

2. Подготовить блок-схему алгоритма и составить программу.

3. Выполнить расчеты на ЭВМ, построить зависимость на ЭВМ. Подготовить отчет.

5.3. Контрольные вопросы.

1. Что называется случайным процессом?

2. Реализация случайного процесса и построение графиков.

3. Формулы для вычисления характеристик случайных процессов (оценка математического ожидания, оценки корреляционных моментов).

4. Формулы для расчета характеристик стационарных случайных процессов.

5. Построение зависимости на EUREKA.

а) Индивидуальные задания.

№№ п/п	t	0	H	2h	3h	4h
x(t1)	x(t2)	x(t3)	x(t4)	x(t5)
1	X1(t)	a,b	a+1,06	a-2,4b	a+2,3b	a-1,8b
2	X2(t)	a+1,2b	a-2,b	a+3,2b	a-1.2b	a-2,2b
3	X3(t)	a-1,b	a+1,2b	a-1,b	a,7b	a+1,2b
4	X4(t)	a,8b	a+1,2b	a-1,4b	a+2,3b	a-1,5b

Варианты

№ вар.	h	a	b	№ вар.	h	a	b

6. Вычисление площадей фигур с помощью метода

статистических испытаний.

(Лабораторная работа №6)

6.1. Краткое описание метода.

Метод статистических испытаний, как численный метод решения математических задач при помощи моделирования случайных величин применяется для решения различных научно-технических задач. Метод позволяет моделировать любой процесс, на которые влияют случайные факторы. Для многих математических задач, не связанных с какими-либо случайностями можно искусственно придумать вероятностную модель, позволяющую решать задачи.

Вычислительный алгоритм имеет простую структуру. Как правило, составляется программа для осуществления одного случайного испытания. Затем это испытание повторяется многократно. Каждый опыт не зависит от всех остальных и результаты всех опытов усредняются.

Метод основан на получении и преобразовании случайных чисел на ЭВМ с различными законами распределения. Доказано, что основную роль играют случайные величины, распределенные по равномерному закону на интервале (0,1). Для получения случайных чисел в языке Паскаль имеется процедура random (10) (выбор случайного числа из 1,2,3,…,9).

Требуется вычислить следующий интеграл.

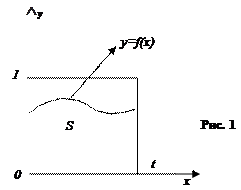0 ≤ f(x) ≤ 1; 0 ≤ x ≤ 1.

Составим квадрат.

Выберем два независимых случайных числа x и y, равномерно распределенных на (0,1) с помощью процедуры random (10)∙0.1. После выбора x и y проверяем условие f(x)<y.

Если да, то увеличиваем значение счетчика (m) количества попавших в область S на единицу и продолжаем эксперимент n раз. Результат .

6.2. Алгоритмы вычисления площади методом Монте-Карло.

а) первый вариант. Составим алгоритм на примере вычисления следующего интеграла .

Составим график функции

f(x)=0.5∙x³-0.3∙x²∙+0.5 (Рис.2)

=max f(x)=60; c = 0 ( для y = 0)

3 ≤ x ≤ 5; n - общее число испытаний

= 3; b = 5 - пределы интегрирования.

1. Входные данные a,b,c,d,n.

2. Подынтегральная функция

f(x)=0.5∙x - 0.3∙x²+0.5.

3. random ize

m= 0 – средние числа показаний случайных чисел в область S.

4. i =1,n.

k1 = random (100)∙0.01 выбор двух случайных чисел из (0,1)

k2 = random (100)∙0.01

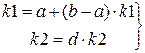преобразование (масштабирование) чисел

K3 = f(k2) - вычислении f(x) для случайного числа k3 из (с,d).

Если k2 < k3 (y < f(x)), то m = m+1 – случайное число k2 находится в области S.

5. S = m/n ∙ (b-a)∙(d-c).

Площадь равна произведению вероятности p = m/n на площадь данного прямоугольника (b-a)∙(d-c).

6. Вывод приближенного значения интеграла S.

б) второй вариант основывается на определениях теории вероятностей. Известно, что математическое ожидание случайной величины x с плотностью P(x) равна значению следующего интеграла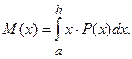

Запишем это применительно к данному интегралу. Имеем

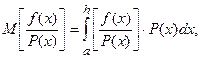где P(x) = 1/(b-a) – плотность равномерного распределения на (a,b), f(x)/P(x) - некоторая случайная величина.

- есть значение определенного интеграла.

Доказано, что для достаточно большого числа … независимых случайных величин z₁,z₂,…,z_n.

(при вероятности P=0.997 ошибка не превосходит .

Алгоритмы метода.

1. Выберем плотность P(x)= 1/(b-a) (равномерное распределение на (a,b)).

2. Исходные данные a,b,n.

3. Подынтегральная функция f(x)=0.5∙x³-0.3∙x³+0.5.

4. S = 0.

5. k1 = random(100)∙0.01 выбор случайного числа на (0,1)

k1=k1∙(b-s) +a –масштабирование случайного числа для отрезка (a,b).

k2=f(k1)/P(k1) – получение новой случайной величины.

S=S+k2 – суммирование случайных величин.

6. 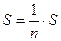– приближенное значение интеграла.

7. Вывод (S). Конец алгоритма.

6.3. Индивидуальные задания.

Таблица 6

вариант №№	a	b	вариант №№	a	b	вариант №№	a	b
1	1	4	10	3	6	19	2	4
2	2	6	11	4	7	20	3	7
3	0	3	12	2	6	21	1	6
4	5	7	13	3	5	22	5	7
5	6	8	14	2	5	23	6	9
6	2	6	15	6	8	24	0	4
7	5	7	16	2	4	25	0	3
8	1	4	17	3	5	26	1	6
9	2	6	18	7	9	27	2	5

Для всех вариантов выполнить расчеты n = 100; n = 1000.

варианты	f(x)
1-5	f(x) =2 x^2 ∙ exp(-x)
6-10	f(x) = ln(x+10)
11-16	f(x) = 0.3 ∙ x^3 + 0.2 ∙ x+5
17-21	f(x) =x^2 +
22-27	f(x) =

6.4. Порядок выполнения лабораторной работы.

1. По варианту выбрать исходные данные и вычислить интеграл на EUREKA. Составить чертеж на EUREKA.

2. Составить блок-схему алгоритма, программу и выполнить расчеты на ЭВМ.

Для первого варианта n = 100; n = 1000; для второго варианта n = 100; n = 1000;

3. Вычислить абсолютные погрешности при n = 100; n = 1000. Подготовить отчет.

6.5. Контрольные вопросы.

1. Постановка задачи метода статистических испытаний.

2. Процедура выбора случайных чисел на ЭВМ.

3. Методика вычисления площади фигур с помощью вероятности попадания точек в область S.

4. Методика вычисления значения определенного интеграла через математическое ожидание вспомогательных чисел.

5. Пояснить расчеты.

Приложение 1.

Распределение Стьюдента.

Значения t_a,n для a=0.1; 0.05;

№	=0.1	=0.05	№	=0.1	=0.05	№	=0.1	=0.05
1	6.31	12.7	12	1.78	2.18	23	1.71	2.07
2	2.92	4.3	13	1.77	2.16	24	1.71	2.06
3	2.35	3.18	14	1.76	2.14	25	1.71	2.06
4	2.13	2.78	15	1.75	2.13	26	1.71	2.06
5	2.01	2.57	16	1.75	2.12	27	1.71	2.05
6	1.94	2.45	17	1.74	2.11	28	1.7	2.05
7	1.89	2.36	18	1.73	2.1	29	1.7	2.04
8	1.86	2.31	19	1.73	2.09	30	1.7	2.02
9	1.83	2.26	20	1.73	2.09	40	1.68	2
10	1.81	2.23	21	1.72	2.08	60	1.67	1.98
11	1.80	2.2	22	1.72	2.07	120	1.66	1.96

Приложение 2

x² – распределение.

Значение функции x² m,a.

m	=0.1	=0.05	m	=0.1	=0.05	m	=0.1	=0.05
1	2.7	3.8	10	16	18.3	19	27.2	30.1
2	4.6	6.0	11	17.3	19.7	20	28.4	31.4
3	6.3	7.8	12	18.5	21.0	21	29.6	32.7
4	7.8	9.5	13	19.8	22.4	22	30.8	33.9
5	9.2	11.1	14	21.1	23.7	23	32.0	35.2
6	10.6	12.6	15	22.3	25.0	24	33.3	36.4
7	12.0	14.1	16	23.5	26.3	25	34.4	37.7
8	13.4	15.5	17	24.8	27.6	26	35.0	38
9	14.7	16.9	18	26.0	28.9	27	35.8	39

Содержание

Стр.

1. Вариационные ряды и их характеристики…………………………………………... (Лабораторная работа №1)……………………………………………………………
2. Расчет характеристик системы случайных величин………………………………. (Лабораторная работа №2)………………………………………………….................
3. Оценка параметров уравнения с помощью метода наименьших квадратов…….. (Лабораторная работа №3)…………………………………………………………..
4. Проверка гипотез о законах распределения……………………………………….. (Лабораторная работа №4)…………………………………………………………..
5. Математический анализ …………………………………………………….
6. Вычисление площадей фигур с случайных процессов…………………………………… (Лабораторная работа №5)…… помощью метода статистических испытаний…... (Лабораторная №6)……………………………………………………………………

Рабадан Рабаданович Таинов

Людмила Владимировна Красовская

Тамара Николаевна Ломаева

Методические указания к выполнению лабораторных работ по дисциплине «Теория вероятностей, математическая статистика и случайные процессы».

Дата добавления: 2014-12-25