Системы счисления и формы представления чисел

ПРЕДСТАВЛЕНИЕ ИНФОРМАЦИИ В ЭВМ

Информация в ЭВМ кодируется, как правило, в двоичной или в двоично-десятичной системе счисления.

Система счисления – это способ наименования и изображения чисел с помощью символов, имеющих определенные количественные значения.

В зависимости от способа изображения чисел системы счисления делятся на позиционные и непозиционные.

В позиционной системе счисления количественное значение каждой цифры зависит от ее места (позиции) в числе. В непозиционной системе счисления цифры не меняют своего количественного значения при изменении их расположения в числе. Количество (Р) различных цифр, используемых для изображения числа в позиционной системе счисления, называется основанием системы счисления. Значения цифр лежат в пределах от 0 до Р- 1. В общем случае запись любого смешанного числа в системе счисления с основанием Р будет представлять собой ряд вида:

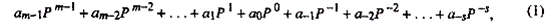
где нижние индексы определяют местоположение цифры в числе (разряд):

§ положительные значения индексов – для целой части числа (т разрядов);

§ отрицательные значения – для дробной (s разрядов),

Пример 4.1. Позиционная система счисления – арабская десятичная система, в которой: основание Р=10, для изображения чисел используются 10 цифр (от 0 до 9). Непозиционная система счисления – римская, в которой для каждого числа используется специфическое сочетание символов (XIV, CXXVII и т.п.).

Максимальное целое число, которое может быть представлено в т разрядах:

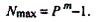
Минимальное значащее (не равное 0) число, которое можно записать в s разрядах дробной части:

Имея в целой части числа т, а в дробной s разрядов, можно записать всего Р ^m+s разных чисел.

Двоичная система счисления имеет основание Р=2 и использует для представления информации всего две цифры: 0 и 1. Существуют правила перевода чисел из одной системы счисления в другую, основанные в том числе и на соотношении (1).

Дата добавления: 2014-12-25