Перемещение формул

В электронной таблице часто перемещают данные из одной ячейки (диапазона ячеек) в другую заданную ячейку (блок ячеек). После перемещения данных исходная ячейка окажется пустой. Это главное отличие перемещения от процесса копирования, в котором копируемая ячейка сохраняет свои данные. Перемещение формул также связано с автоматической подстройкой входящих в нее адресов операндов. При перемещении формул, так же как при их копировании, действует правило относительной ориентации клеток. Поэтому после перемещения относительное расположение клеток, содержащих перемещенную формулу и исходные данные (заданные относительными адресами), сохраняется таким же, как в формуле-оригинале.

Пример 14.13. На рис. 14.3 а мы видим перемещение содержимого отдельной ячейки A3 в ячейку С3. В этом случае содержимое исходной ячейки, не изменяясь, перемещается в ячейку назначения, а исходная ячейка остается пустой. Рис. 14.3 б иллюстрирует случай перемещения содержимого трех ячеек A1, A2 и A3. При этом ячейки взаимосвязаны – содержимое третьей ячейки включает в себя содержимое первых двух. После перемещения мы видим, что в результате автоматической подстройки ссылок содержащаяся в ячейке A3 формула изменилась, чтобы отразить произошедшие в электронной таблице изменения (теперь компоненты содержащейся в ячейке С3 суммы находятся в других ячейках). Так же как и в предыдущем случае диапазон исходных ячеек после выполнения операции перемещения опустел.

На рис. 14.3 в мы видим перемещение содержимого ячейки A3 в ячейку С3, когда адрес переносимой ячейки входит в другую формулу. Это случай перемещения зависимых ячеек. Например, имеется дополнительная ячейка В1, содержимое которой зависит от содержимого перемещаемой ячейки A3. В данном случае содержимое перемещаемой ячейки не изменяется, но изменяется содержимое зависимой ячейки В1 (хотя она не перемещается). Автоматическая подстройка адресов и в данном случае отразит изменения в электронной таблице так, чтобы результат формулы, содержащейся в ячейке В1, не изменился.

Последний случай, не рассмотренный на рис. 14.3, связан с возможностью использования абсолютных адресов. Нетрудно заметить, что использование абсолютных адресов при выполнении команды перемещения не имеет смысла, поскольку над ними также выполняется автоматическая подстройка адресов для отражения изменений, происходимых в таблице.

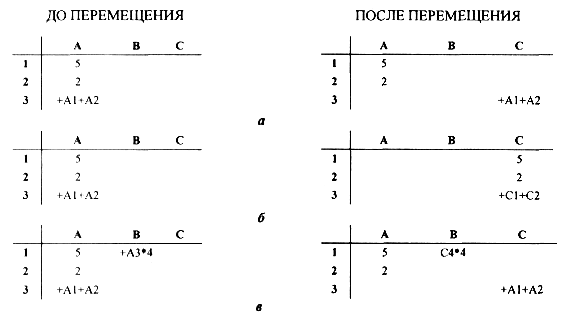
Рис. 14.3. Перемещение содержимого ячеек: а – одной ячейки; б – колонки; в – зависимых ячеек

В целом команда перемещения является непростой командой, и вам следует хорошо подумать, прежде чем перемещать формулы и функции, содержащие ссылки. При перемещении символьных данных никаких трудностей не возникает.

Дата добавления: 2014-12-25