ГОСТ 2.303-68 – Линии

Лист 6

Лист 5

Лист 4

Лист 3

Лист 2

Лист 1

Контрольная работа

Экзамен

На экзамен допускаются студенты, у которых зачтена контрольная работа и выполнены все аудиторные работы. Экзамен проводится по билетной системе. На экзамене студент должен решить задачу и ответить в графической форме на теоретический вопрос экзаменационного билета. Кроме того, экзаменатору предоставляется право задавать дополнительные вопросы.

Формат А3. Выполняется титульный лист контрольной работы в соответствии с рисунками 1-5.

Формат А3. Основная надпись по форме 6а. Выполнить две задачи по теме «Точка, прямая, плоскость в ортогональных проекциях». Пример выполнения листа приведен на рисунке 9. Для левой и правой частей листа координатные оси показывать раздельно. На листе 2 и остальных листах контрольной работы обводку решенных задач можно выполнять цветной пастой шариковой ручкой или тушью. Четко различать видимые и невидимые линии чертежа: видимые - сплошные основные 0,6…0,8 мм; невидимые - штриховые 0.4…мм. Черной пастой обводят исходные данные, красной - полученный результат решения. Все промежуточные построения должны быть показаны на чертеже тонкими линиями 0,1…0,2 мм различными цветами (синим, зеленым, коричневым и т.д.) в зависимости от принадлежности к этапу решения задачи. Все вспомогательные построения не стирать и все точки чертежа обозначить.

Задача 1. Дано: плоскость треугольника a (А, В, С) и точка D. Требуется определить расстояние от точки D до плоскости, заданной, треугольником a (А, В, С). Определить видимость перпендикуляра, проходящего через точку D, и плоскости треугольника a (А, В, С). Данные для выполнения задачи взять из таблицы 1 в соответствии с вариантом.

Указания к задаче 1. Задачу выполняют в такой последовательности:

1) из точки D опустить перпендикуляр b (b₁,b₂), используя горизонталь h и фронталь f плоскости. При этом горизонтальная проекция перпендикуляра b₁ перпендикулярна горизонтальной проекции горизонтали h₁, а фронтальная проекция перпендикуляра b₂ перпендикулярна фронтальной проекции фронтали f₂;

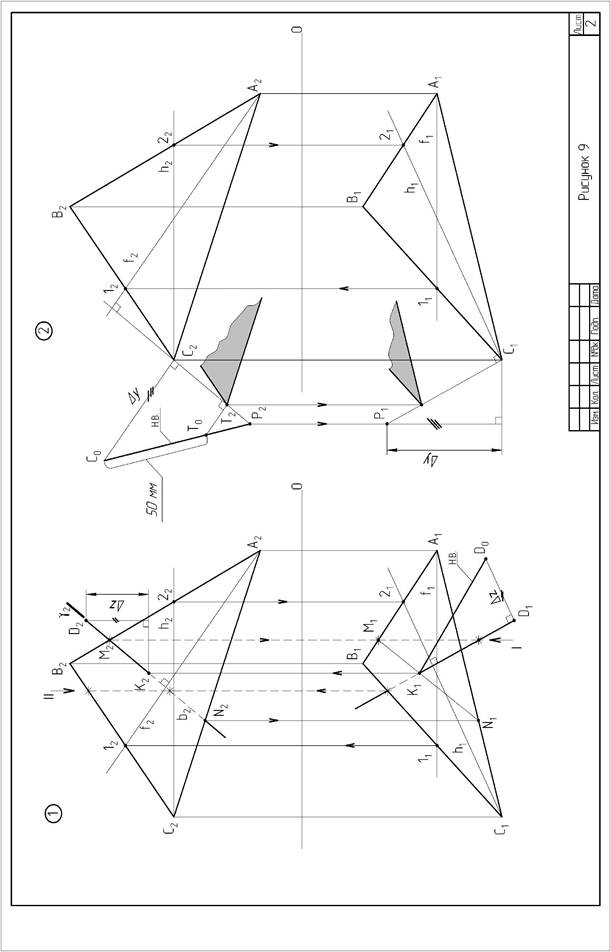
2) определить точку пересечения перпендикуляра с плоскостью a (А, В, С), для чего перпендикуляр (прямую) заключают во вспомогательную, обычно проецирующую, плоскость (Y), находят линию пересечения плоскости a (А, В, С) и вспомогательной плоскости (Y), отмечают точку К (К₁,К₂) в которой эта линия пресекается с перпендикуляром;

3) определяют натуральную величину (Н.В.) расстояния от точки D до плоскости a (А, В, С), применяя способ прямоугольного треугольника;

4) видимость проекции перпендикуляра определяют методом конкурирующих точек.

Таблица 1

Номер варианта

Значения координат, мм

АХ

АY

АZ

ВХ

ВY

ВZ

СХ

СY

СZ

DХ

DY

DZ

Задача 2. Дано: плоскость треугольника a (А,В,С). Требуется: построить плоскость, параллельную заданной и отстоящую от неё на 45…50 мм. Данные для выполнения задачи взять из таблицы 1.

Указания к задаче 2. Задачу выполняют в такой последовательности:

1) в заданной плоскости a (А, В, С) выбирают произвольную точку (в том числе вершину, на рисунке 9 взята точка С) и из неё восстанавливают перпендикуляр к плоскости a (А,В,С) (аналогично действию первому в первой задаче);

2) определяют методом прямоугольного треугольника натуральную величину произвольного отрезка перпендикуляра, который ограничивают произвольной точкой Р;

3) на натуральной величине произвольного отрезка перпендикуляра находят

точку Т, расположенную на заданном расстоянии 45 мм от плоскости, и строят проекции этой точки на проекциях перпендикуляра;

4) через точку Т строят исходную плоскость, соблюдая условие параллельности плоскостей: если плоскости параллельны, то две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости. На эпюре одноименные проекции пересекающихся прямых параллельны.

Задача 1 (формат А3). Основная надпись по форме 6а. Построить линию пересечения треугольников ABC и EDK и показать видимость их в проекциях.

Определить натуральную величину треугольника АВС. Данные взять из таблицы 2. Пример выполнения листа приведен на рисунке 10.

Указания к задаче 1. В левой половине листа намечают оси координат и из таблицы 2 согласно своему варианту берутся координаты точек A, B, C, D, E, K вершин треугольника (рисунок 10). Стороны треугольников и другие вспомогательные прямые проводятся вначале тонкими сплошными линиями. Проекции линии пересечения треугольников строятся по точкам пересечения сторон одного треугольника с другим или по точкам пересечения каждой из сторон одного треугольника с другим порознь. Такую линию можно построить, используя и вспомогательные секущие проецирующие плоскости.

Видимость сторон треугольника определяется способом конкурирующих точек. Видимые отрезки сторон треугольников выделяют сплошными толстыми линиями, невидимые следует показать штриховыми линиями. Определяется натуральная величина треугольника АВС.

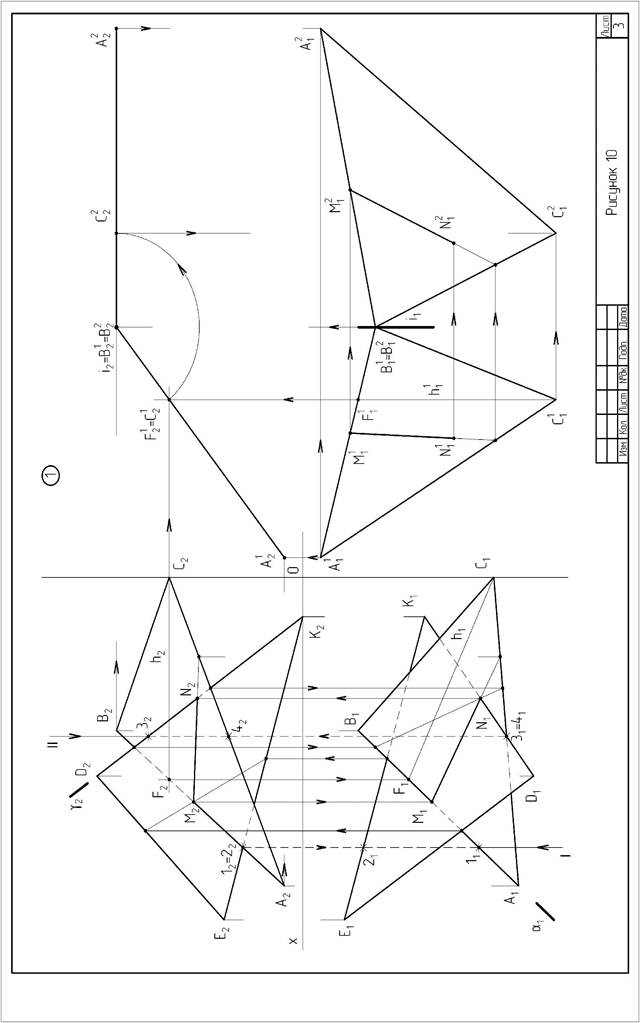
Плоскопараллельным перемещением треугольник АВС переводится в положение проецирующей плоскости и далее вращением вокруг проецирующей прямой в положение, когда он будет параллелен плоскости проекций.

В треугольнике АВС следует показать и линию МN пересечения его с треугольником EDK.

Все вспомогательные построения должны быть показаны на чертеже тонкими линиями, а условие задачи и ее результат – толстыми.

Таблица 2

Номер варианта

Значения координат, мм

АХ

АY

АZ

ВХ

ВY

ВZ

СХ

СY

СZ

DХ

DY

DZ

ЕХ

ЕY

ЕZ

КХ

КY

КZ

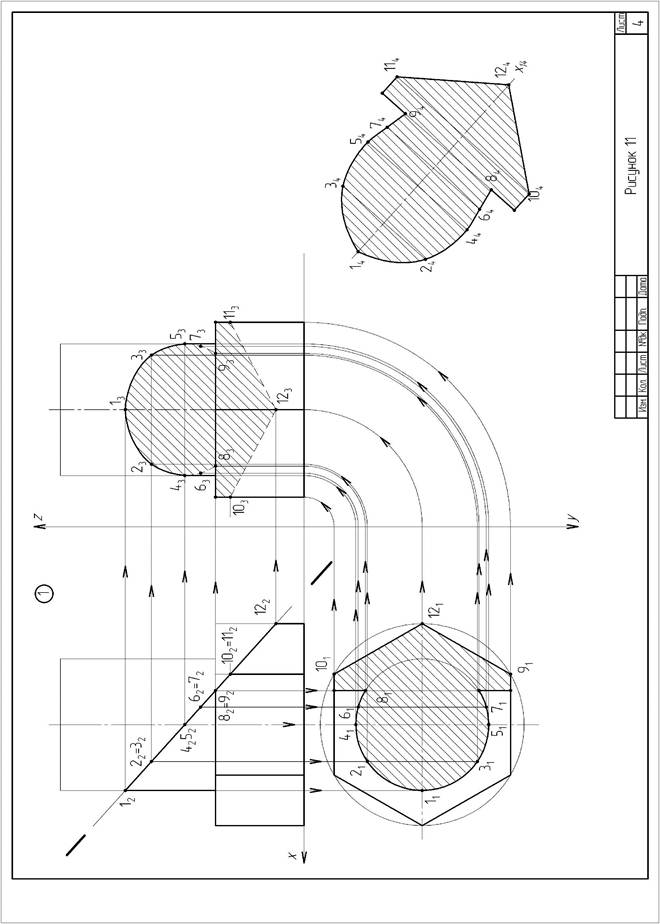
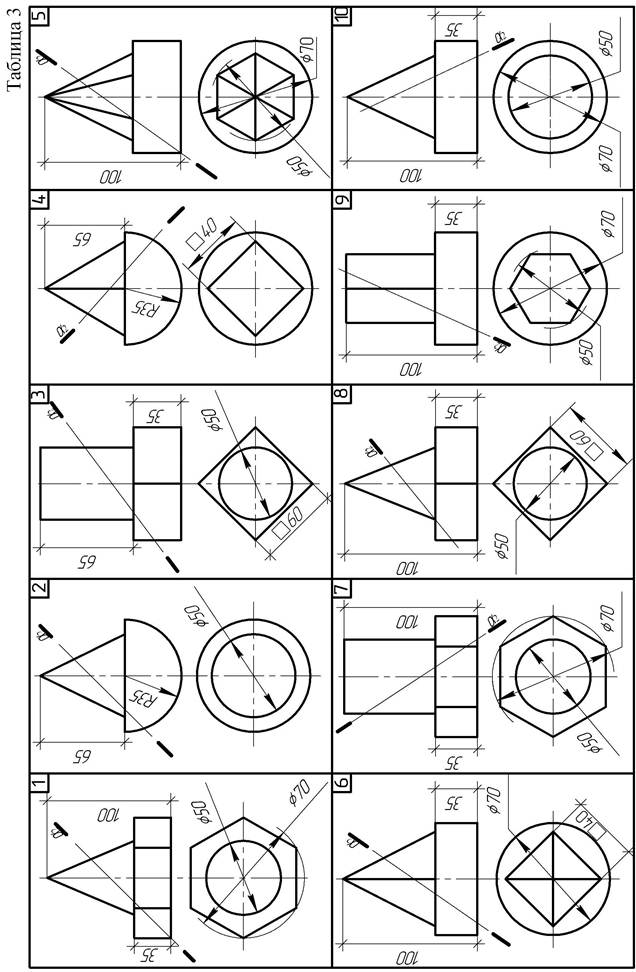
Задача 1. Формат А3. Основная надпись по форме 6а. Построить три проекции линии пересечения сложной поверхности с фронтально-проецирующей плоскостью и способом совмещения (вращения вокруг линии уровня) определить натуральную величину этого сечения. Данные для вычерчивания комбинированной поверхности берут из таблицы 3. Пример выполнения листа приведен на рисунке 11.

Указания к задаче 1. Высота всей комбинированной поверхности равна 100 мм, нижняя ее часть - 35 мм. Размеры диаметров оснований поверхностей и вспомогательных окружностей, а также стороны многоугольников приведены в таблице 3. Положение секущей плоскости для своего варианта студент назначает самостоятельно. Задачу решают в три этапа:

1) строят проекции сечения;

2) определяют натуральную величину сечения указанным способом;

3) выполняют обводку оставшейся части сложной поверхности.

Так как в данном задании для пересечения предложена плоскость частного положения – фронтально-проецирующая, то решение задачи сводится к построению проекций ряда точек фигуры сечения заданной поверхности как точек, расположенных на образующих или направляющих линиях этой поверхности. Первоначально крайние и промежуточные точки сечения назначаются на следе секущей плоскости. Натуральную величину сечения определяют по тем же точкам, которые были установлены на первом этапе.

За ось вращения плоскости сечения выбирают фронталь плоскости сечения, совпадающую с его осью симметрии. Для того чтобы избежать наложения изображений, фронталь следует размещать на свободном поле чертежа параллельно следу секущей плоскости. Каждая точка сечения будет вращаться вокруг оси в плоскости, перпендикулярной ей. Радиус вращения отображен в натуральную величину на горизонтальной плоскости проекций и соответствует расстоянию от точки до продольной оси симметрии (оси вращения).

Формат А3. Основная надпись по форме 6а. Выполнить две задачи по теме «Взаимное пересечение поверхностей». Пример выполнения листа см. на рисунке 12.

Задача 1. Дано: многогранник и кривая поверхность. Требуется: способом вспомогательных секущих плоскостей построить линию пересечения многогранной и кривой поверхностей, выделив ее видимые и невидимые участки. Данные для выполнения задачи взять из таблицы 4.

Указания к задаче 1. Задачу выполняют на левой половине листа в такой последовательности: 1) намечают расположение вспомогательных секущих плоскостей частного положения (уровня) или проецирующих; 2) с их помощью определяют характерные и промежуточные точки линии пересечения поверхностей; 3) полученные точки соединяют плавными кривыми линиями, установив предварительно последовательность расположения точек на линии пересечения поверхностей. Видимую часть линий контура, в том числе и линии пресечения, обводят сплошной основной, а невидимую – штриховой линиями. При решении задач на взаимное пересечение поверхностей следует помнить следующие положения.

1. Чтобы построить точку, принадлежащую линии пересечения поверхностей, нужно обе поверхности рассечь вспомогательной плоскостью и, найдя линии пересечения вспомогательной плоскости с заданными поверхностями, отметить общие для них точки.

2. Плоскость следует выбирать так, чтобы линии ее пересечения с поверхностями проецировались в простейшие фигуры (окружности или прямые). Использование нескольких вспомогательных плоскостей позволяет определить ряд точек линии пересечения. Соединять можно только те точки, которые расположены в одной грани многогранника.

3. Когда боковая поверхность цилиндра или призмы занимает относительно плоскости проекций проецирующие положение (образующие цилиндра или ребра призмы перпендикулярны этой плоскости проекций), то одна проекция линии пересечения поверхностей становится известной без дополнительных построений – она совпадает с проекцией поверхности.

Задача 2. Построить линию пересечения конуса вращения с цилиндром вращения. Оси поверхностей вращения – взаимно перпендикулярные проецирующие скрещивающиеся прямые. Данные для своего варианта взять из таблицы 5.

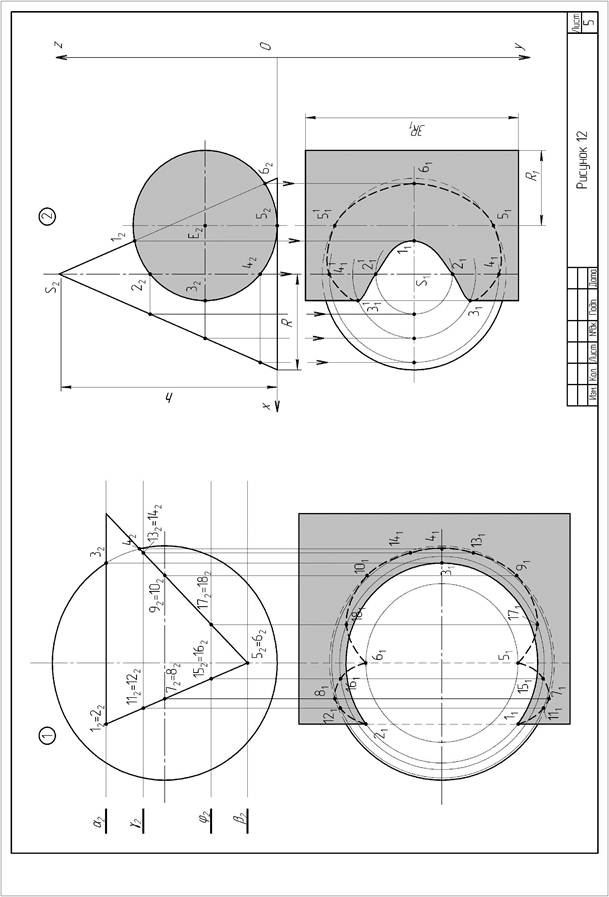
Указания к задаче 2. В правой части листа намечают оси координат и из таблицы 5 берут согласно своему варианту величины, которыми задаются поверхности конуса вращения и цилиндра вращения. Определяют центр (точка К) окружности радиуса R основания конуса вращения в горизонтальной координатной плоскости. На вертикальной оси на расстоянии h от плоскости уровня и выше определяют вершину конуса вращения.

Осью цилиндра вращения является фронтально-проецирующая прямая точки Е; основаниями цилиндра являются окружности радиуса R₁. Образующие цилиндра имеют длину, равную 3R₁, и делятся пополам фронтальной меридиональной плоскостью конуса вращения.

С помощью вспомогательных секущих плоскостей определяют точки пересечения очерковых образующих одной поверхности с другой и промежуточные точки линии пересечения поверхностей. Проводя вспомогательную секущую плоскость фронтальную меридиональную плоскость конуса вращения, определяют точки пересечения главного меридиана (очерковых образующих) конуса вращения с параллелью (окружностью) проецирующего цилиндра. Выбирая горизонтальную секущую плоскость, проходящую через ось цилиндра вращения, определяют две точки пересечения очерковых образующих цилиндра с поверхностью конуса.

Высшую и низшую, а также промежуточные точки линии пересечения поверхности находят с помощью вспомогательных горизонтальных плоскостей – плоскостей уровня. По точкам строят линию пересечения поверхности конуса вращения с цилиндром вращения и устанавливают ее видимость в проекциях.

Таблица 5

Номер варианта	Значения, мм
КХ	КY	КZ	R	h	ЕХ	ЕY	ЕZ	R1

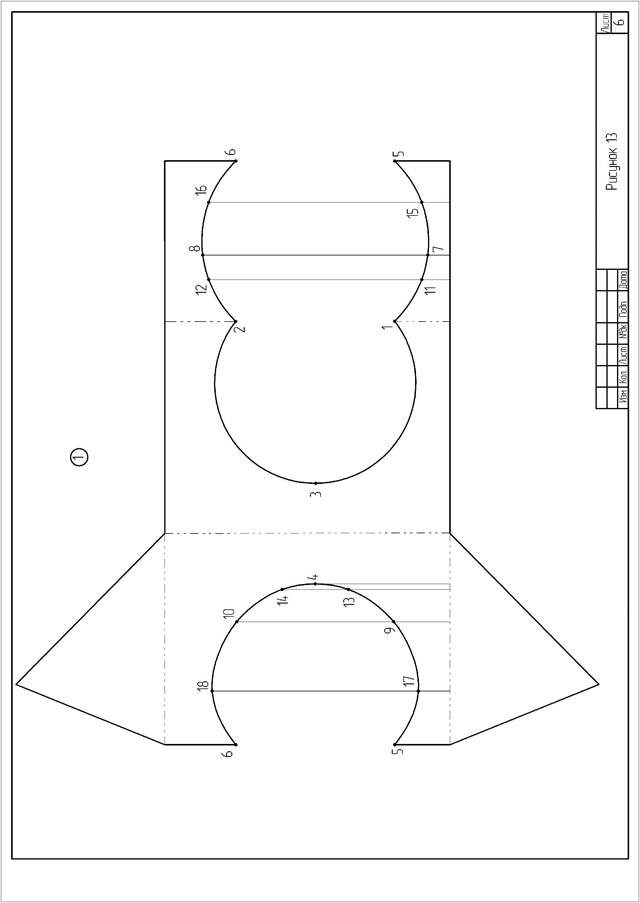
Задача 1. Формат А3. Основная надпись по форме 6а. Выполнить развертку призмы из задачи 1 листа 5. Показать на развертке линию пересечения призмы с поверхность вращения. Пример оформления листа дан на рисунке 13.

Указания к задаче 1. Порядок выполнения развертки призмы приведен в приложении 3. Линии сгиба на развертке показать штрихпунктирной линией с двумя точками.

Приложение 1

Начертание и назначение линий на чертежах

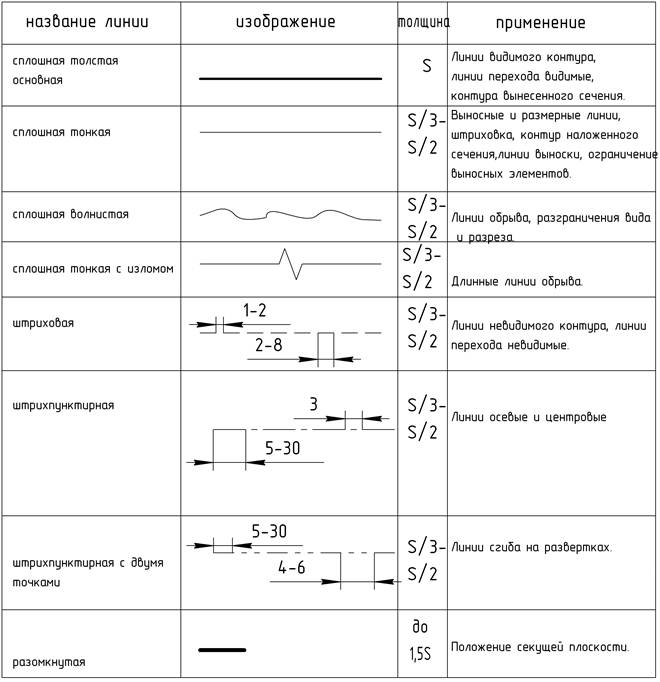
Толщина сплошной основной линии должна быть в пределах от 0,5 до 1,4 мм в зависимости от размеров и сложности изображения, а также от формата чертежа.

Приложение 2

ГОСТ 2.304-81 – Шрифты чертежные

Чертежный шрифт содержит русский, латинский и греческий алфавиты, арабские и римские цифры, а также знаки.

Размер шрифта определяется высотой прописных букв, мм: 2,5; 3,5; 5; 7; 10; 14; 20; 28; 40.

Приложение 3

Рассмотрим построение развертки прямой призмы (рисунок 1), основание которой принадлежит горизонтальной плоскости проекций.

Т.к. нижнее основание призмы находится в плоскости П₁, а верхнее параллельно ей, то в горизонтальной плоскости проекций они изображаются в натуральную величину.

Боковые грани призмы – прямоугольники. Ширина прямоугольника соответствует какой-либо стороне основания призмы, а высота – высоте призмы.

Последовательность построений:

1. На свободном месте чертежа проводим горизонтальную прямую а, выбираем на ней произвольную точку, принадлежащую основанию, например точку А (рисунок 2).

2. Через точку А проводим прямую b, перпендикулярную прямой а, и откладываем на этой прямой высоту призмы или длину ребра [A₂A^|₂].

3. Через точку А^| проведем горизонтальную прямую с.

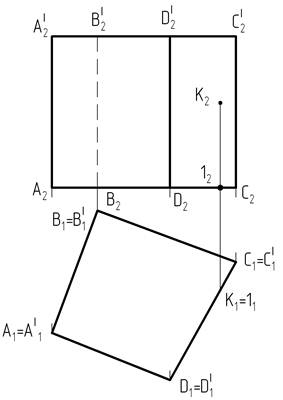
Рисунок 1

Рисунок 2

4. От точек А и А^| на прямых а и с соответственно отложим длину отрезка [A₁B₁], получим точки В и В^| (рисунок 3).

5. От точек В и В^| на прямых а и с соответственно откладываем длину отрезка [B₁C₁], получаем точки С и С₁.

6. На прямых а и с от точек С и С₁ отложим отрезки равные длине отрезка [C₁D₁]. Построили точки D и D^|, от которых отступаем расстояние, равное |D₁A₁|. Нашли положение точек А и А^|.

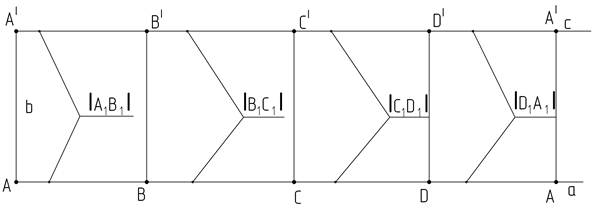
Рисунок 3

7. Соединяем точки, найденные на прямой а с соответствующими точками, лежащими на прямой с. Получаем развертку боковой поверхности призмы.

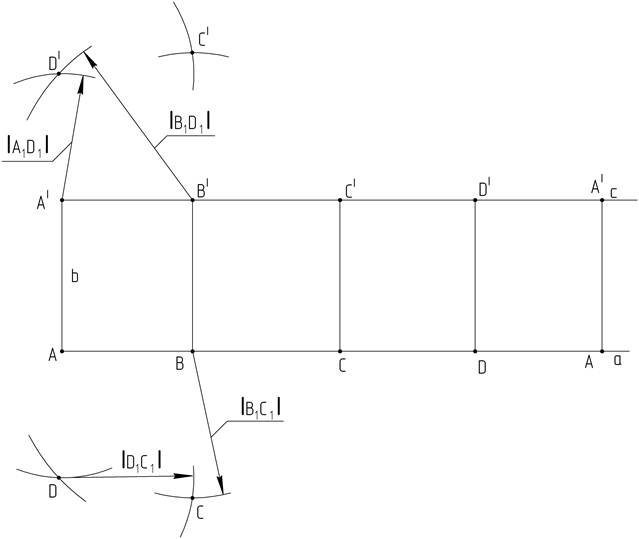
Рисунок 4

8. Построим основания призмы. Через точки А и А^| проведем дуги радиусом, равным длине отрезка [A₁D₁], а через точки В и В^| - |В₁D₁|. На пересечении дуг будут находится точки D и D^|. На рисунке 4 показано построение для точки D^|.

9. Найдем положение точек С и С^|. Через точки В и В^| проведем дуги, радиусом |В₁С₁|, а через точки D и D^| - |D₁C₁|, на пересечении дуг будут находится искомые точки. На рисунке 4 показано построение для точки С.

10. Обводим контур построенной фигуры сплошной толстой линией, а линии сгиба – штрихпунктирной с двумя точками (рисунок 5).

11. Построим точку К (рисунок 1), принадлежащую грани (DD^|C^|C) на развертке. От точки С отложим длину отрезка [C₁1₁], получим т.1 на развертке.

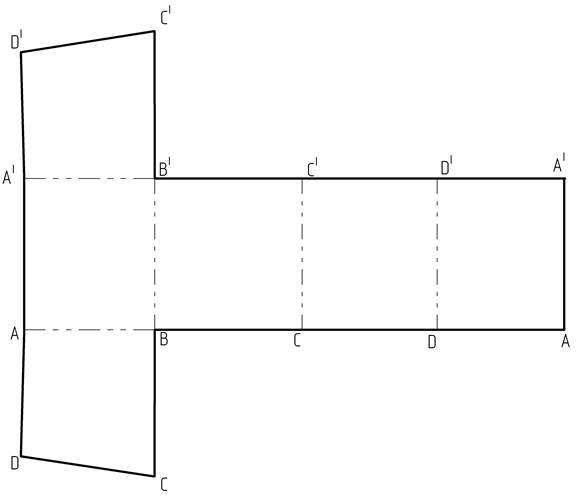
Рисунок 5

12. Через точку 1 проведем вертикальную прямую (прямую параллельную ребру [CC^|] и отложим на ней расстояние |1₂К₂|, тем самым мы найдем искомую точку К (рисунок 6).

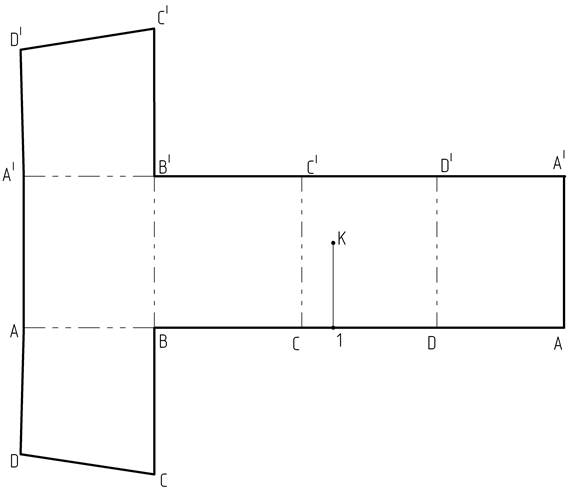
Рисунок 6

Замечание. В данном примере поверхность призмы совмещена с плоскостью своей наружной стороной.

Список рекомендуемой литературы

для выполнения контрольной работы и подготовки к экзамену:

1. Гордон В.О., Семенцов-Огиевский М.А. Курс начертательной геометрии: Учебное пособие для вузов.- Изд.-24-е. – М.: Высш. шк., 1998.-272 с.

2. Гордон В.О., Семенцов-Огиевский М.А. Сборник задач по курсу начертательной геометрии. – М.: Высш. шк., 1998. -112 с.

3. Иванов Г.С. Начертательная геометрия: Учебник. – М.: Машиностроение, 1995. – 224 с.

4. Локтев О.В. Краткий курс начертательной геометрии. Учебное пособие для вузов. – Изд. – 3-е. –М.: Высш. шк., 1999.-136 с.

5. Локтев О.А. Задачник по начертательной геометрии. Учебное пособие для вузов. – М.: Высш. шк., 1999

6. Начертательная геометрия. Учебник для вузов / Н.Н.Крылов, С.Г.Иконникова, В.Л.Николаев, В.Е.Васильев; ред. Н.Н.Крылов. – 7-е изд., перераб. и допол. – М.: Высш. шк., 2001. -223 с.

7. Павлова, А.А. Начертательная геометрия: учебник для педагогических вузов. – М.: Прометей, 1993. -280 с.

8. Тарасов Б.Ф. Начертательная геометрия: Учебник. – 5-е изд., стер., - СПб: Лань, 2005. – 256 с., ил.

Дата добавления: 2014-12-25