Постановка экспериментальной задачи

В данной работе осуществляется экспериментальная проверка основного уравнения динамики вращательного движения (4.8) с помощью маятника Обербека. Маятник представляет собой маховик, которому придана крестообразная форма (рис. 4.1).

По четырем взаимно-перпендикулярным стержням могут перемещаться грузы массой m ₀. На общей оси находится шкив, на который наматывается нить с привязанным к ней грузом массой m. Под действием падающего груза нить разматывается и приводит маховик в равноускоренное вращательное движение. При этом угловое ускорение крестовины определяется соотношением:

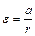, (4.9)

где а – ускорение падающего груза, r = d/ 2 – радиус шкива.

В свою очередь, пользуясь известным выражением для равноускоренного движения груза:

, (4.10)

(h – высота падения груза, t – время падения груза) находим:

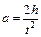, (4.11)

или, используя (4.9):

. (4.12)

Момент силы, приложенной к маятнику, находим по формуле (4.7), где F – сила, действующая на шкив. Но 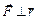, и 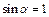. Тогда формула (4.7) имеет вид: .

Силу F можно найти из уравнения движения груза:

, (4.13)

где m – масса падающего груза, а , – сила натяжения нити. Тогда для момента силы получим следующее выражение:

. (4.14)

Используя формулу (4.8) получим:

. (4.15)

Определив экспериментально значения h и t, при заданных параметрах r и m, по формуле (4.15) находим значение момента инерции маятника Обербека. Теоретическое значение момента инерции маятника можно рассчитать следующим образом:

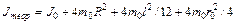, (4.16)

где m ₀ = 0,114 кг – масса подвижного груза крестовины; R – расстояние от центра масс подвижного груза до оси вращения; r ₀= 0,015 м – радиус груза; l = 0,02 м – длина образующей груза. Момент инерции системы без грузов J ₀ можно определить по формуле:

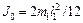, (4.17)

где l ₁ = 0,15 м – длина одного из стержней крестовины; m ₁= 0,023 кг – масса стержня.

Дата добавления: 2014-12-25