Математическое моделирование управления процессами и технологией

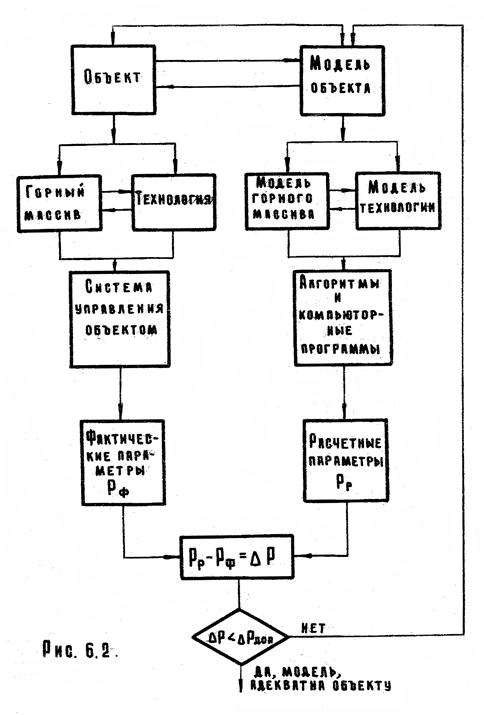
При решении задач управления процессами и технологии во взаимосвязанном комплексе "Технологическая система - Среда." важным является создание адекватной математической модели для прогноза геомеханических параметров среды. Для этого необходимо осуществить настройку (адаптацию) модели с учетом фактических данных о параметрах горного массива и

технологической системы в ходе их взаимодействия. На рис. 6.2. представлена схема взаимодействия объекта (массива горных пород и технологии) и математических моделей их управления. Суть адаптивного моделирования заключается в следующем.

Исследуемый объект состоит из двух блоков: горный массив и технология. Параллельно с объектом действует приобъектная математическая модель, которая включает модель горного массива и модель технологических процессов.

Воздействие в технологической системе в виде реакции оказывает влияние на эффективность работы горной техники, процессы деформирования крепи и др. Человек, принимая управляющее решение, компенсирует негативное воздействие горного массива на технологию путем изменения параметров системы разработки, формы, размеров забоев и крепи горных выработок, режимов выемки и др. Такой процесс непрерывкой корректировки взаимодействия горного массива и технологии осуществляется системой управления, которая включает комплекс технических реакций на процесс функционирования объекта. Их результатом являются фактические параметры.

Ядром приобъектной модели являются алгоритмы и компьютерные программа, которые должны не только адекватно формализовать реальный горный массив и технологию в статике, но и обеспечить описание процессов взаимодействия между ними. Также как и система управления объектом, алгоритмы и программное обеспечение должны быть мобильными и отражать управляющие воздействия на объект. Результатом моделирования являются расчетные параметры.

Критерием адекватности модели и реального объекта может быть принята разность DР между фактическими и расчетными параметрами. Следует отметить, что количество расчетных параметров, как правило, больше, чем фактических. Если разность между фактическими параметрами больше допустимой DР_доп то осуществляется корректировка модели, если меньше - можно приступать к решению задач управления параметрами объекта. Математические модели рассмотренного типа называются адаптивными моделями.

Контрольные вопросы и задачи

1. Что такое математическая модель процесса?

2. Чем отличаются оптимизационные и информационные модели?

3. Дать общую постановку задачи оптимизации.

4. В чем различие методов линейного нелинейного и динамического программирования?

5. Основные методы, используемые при построении информационных моделей.

6. Этапы построения математической модели.

7. Методы упрощения моделей.

8. В чем заключается предварительный контроль математической модели?

9. Идея метода Монте-Карло.

10. Составить обобщенный алгоритм имитационного моделирования случайных процессов.

11. Как формируются случайные числа с заданным законом распределения?

12. Физическая природа критерия адаптации

13. Пример вычисления критерия адаптации технологической системы шахты.

14. Составить и объяснить алгоритм построения адаптивных математических моделей управления технологическими процессами.

15. Критерий адекватности математической модели и реального объекта.

Контрольная работа № 7

Номер по списку

Вопросы, задачи

РАЗДЕЛ ТРЕТИЙ

ФИЗИЧЕСКОЕ МОДЕЛИРОВАНИЕ ГОРНЫХ ПРОЦЕССОВ

Дата добавления: 2014-12-25