
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Методы анализа Марковской модели принятия решений
|
|
|
|
2.1 Применение метода прямого перебора для анализа Марковской модели принятия решений при бесконечном количестве этапов.
При бесконечном количестве этапов мы предполагаем, что с течением времени система переходит в стационарный режим.
Для стационарного режима определены вероятности состояний при реализации U-й стратегии πi(u).
При этом на основе матрицы решений D(Z) вычислены матрицы выигрышей для стационарных стратегий D(U). D(Z) →D(U)
Необходимо выбрать такую стационарную стратегию, которая бы обеспечила максимальный суммарный выигрыш за нахождение системы в каждом i-м состоянии.
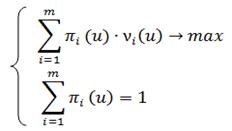
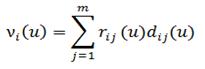
- эта величина выигрыша при нахождении системы в i-том состоянии при реализации некой u-той стационарной стратегии.
В качестве критерия применяется величина выигрыша за один этап, и этот выигрыш определяется как сумма выигрышей по всем состояниям.
Таким образом, алгоритм решения задачи основан на идее полного перебора всех возможных стационарных состояний и вычислении для них значения суммарного критерия эффективности.
В качестве оптимальной выбирается такая стационарная стратегия, для которой значение функционала будет максимальным.
Таким образом для задачи полного перебора в исходные данные включены множеств общих стратегий z={1,2,…z…p} соответственно матрица переходных вероятностей R(z) и матрица стоимостей из состояния i в состояние j D(z).
Далее из общей стратегии справедливым условием, что z є Z.
Первый шаг алгоритма – в соответствии с общим числом стратегий p и общего числа состояний m формируется множество стационарных стратегий.
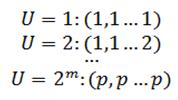
Делаем полный перебор всех ситуаций.
Второй шаг – для каждой из сформированных стационарных стратегий по матрицам конструируются матрицы принятых решений R(Z)→R(U), D(Z)→D(U). Очевидно, что количество переходов R(U) и количество выигрышей D(U)будет равно pm.
Третий шаг – для каждой стационарной стратегии находится вектор стационарного распределения вероятностей 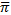 (u)=[π1(u),π2(u)…πi(u)…πm(u)]. Для нахождения вектора
(u)=[π1(u),π2(u)…πi(u)…πm(u)]. Для нахождения вектора  (u) используется система линейных уравнений, представленная в матричной форме
(u) используется система линейных уравнений, представленная в матричной форме
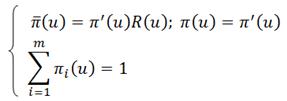
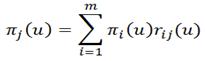
Решение системы линейных уравнений может быть выполнено либо методом подстановки, либо на основе приведения системы уравнений к канонической форме. Ах=В.
Четвертый шаг – для каждой из стационарных стратегий необходимо найти значение выигрышей за один этап функционирования системы.
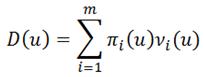
Где опять же νi(u) – выигрыш за пребывание системы в i-м состоянии при реализации u-й стратегии.
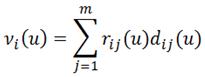
Основной недостаток метода прямого перебора состоит в том, что при увеличении числа состояний m и количества общих стратегий p, число стационарных стратегий существенно возрастает. Поэтому для задач большой размерности применяется метод динамического программирования для анализа Марковской модели.
2.2. Постановка задачи – рассматривается система, которая соответствует следующей базовой концептуальной модели.

Количество этапов N ограничено. Задано множество стратегий Z={1,2…z…p}, задана матрица вероятности переходов R(Z) и матрица выигрышей D(Z). Необходимо для каждого состояния на каждом из этапов найти оптимальные общие стратегии, которые обеспечивают максимальный локальный выигрыш.
Для решения этой задачи введем функцию fn(i), которая означает оптимальный выигрыш для i-того состояния за n-1, n, n+1 этапы функционирования.
Для данной модели уравнение Беллмана представляется следующим образом
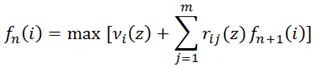
νi(z) - выигрыш от пребывания системы в i-м состоянии при реализации общей стратегии Z.
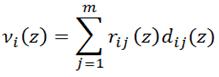
Этот выигрыш при реализации алгоритма обратной прогонки, если известно количество этапов и оно ограничено N, то для решения уравнения Беллмана целесообразно применить алгоритм обратной прогонки.
В этом случае решение производится начиная с последнего этапа принятия решений, то есть n=N и fN(i)=max{νi(z)}
На следующем шаге рассматривается решение принятое на предпоследнем этапе, то есть n=N-1. В этом случае уравнение Беллмана
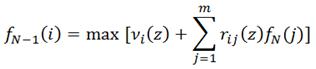
Где νi(z)– выигрыш от пребывания системы в i-м состоянии при реализации общей стратегии Z и в этом решении учитывается значение функции fN(j), найденное в предыдущем решении. Функционал fN-1(i) представляет собой локальный выигрыш, получаемый при функционировании системы за n-1 и n этапы. Аналогичные уравнения составляются для остальных шагов до первого шага включительно. После этого производится просмотр полученных таблиц в прямом порядке для нахождения безусловных оптимальных стратегий.
|
|
|
|
|
Дата добавления: 2014-12-25; Просмотров: 452; Нарушение авторских прав?; Мы поможем в написании вашей работы!