Перетворення стиснення

Строение периферического отдела

Тема. Строение слуховой сенсорной системы

Вопросы:

1. Периферический отдел слуховой системы: строение внешнего, среднего и внутреннего уха.

2. Ход проводящих путей слуховой сенсорной системы.

3. Корковый отдел.

Литература

1. Нейман Л.В., Богомильский М.Р. Анатомия, физиология и патология органов слуха и речи. М., 2003.

2. Слуховая система. Ред. Я.А. Альтман. Л., 1990.

Слуховая сенсорная система состоит из 3 отделов: периферирический, проводниковый, корковый.

Периферический отдел представлен наружным, средним, внутренним ухом (рисунок 1).

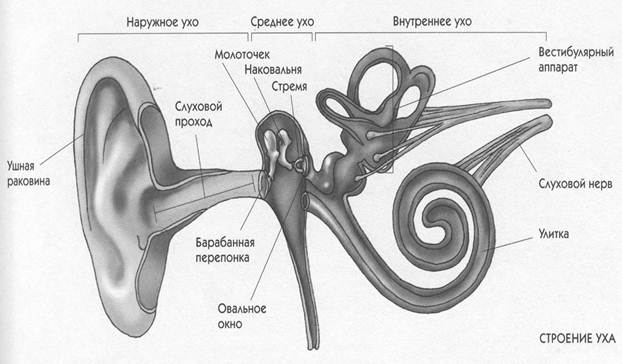
Рисунок 1. Строение уха

Рисунок 2. Строение барабанной перепонки

Рисунок 3. Строение слуховых косточек

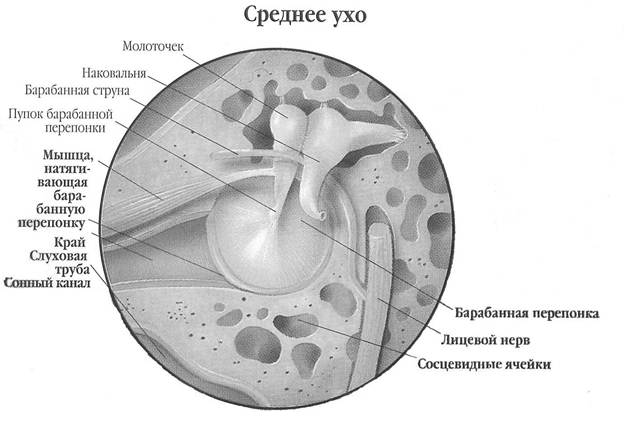
Рисунок 4. Строение среднего уха.

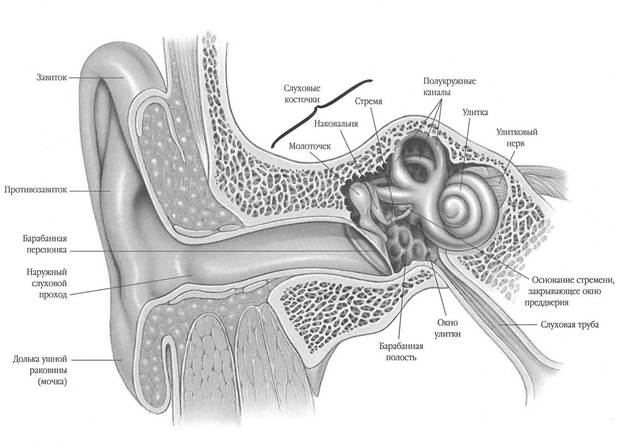
Рисунок 5. Строение уха

Під перетворенням стиснення до координатної площини Oxz будемо розуміти таке перетворення, при якому точка 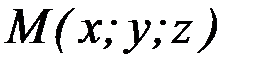переходить в точку 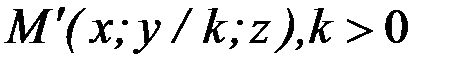. Параметр k називають коефіцієнтом стиснення.

При k > 1 точки простору, розташовані на одній прямій, яка перпендикулярна площині Oxz зближуються, тобто перетворення ― дійсно стиснення.

При 0 < k <1 перетворення фактично є розтягуванням.

Нехай в просторі в прямокутній системі координат Oxyz деяка множина Q задано своїм рівнянням . При перетворенні стиснення до координатної площини Oxz з коефіцієнтом k ця множина перетворюється в нову множину 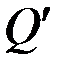з рівнянням .

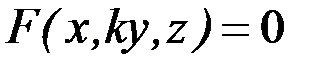16.4. Еліпсоїди

Поверхня, що утворюється при обертанні еліпса навколо однієї з його осей симетрії, називають еліпсоїдом обертання (рис.16.3)

Рівняння еліпсоїда обертання виведемо, розташувавши початок прямокутної системи координат у центрі еліпса і поєднавши вісь аплікат Oz з віссю обертання, а координатну площину Oxz - з площиною еліпса (рис.16.4). Тоді рівняння еліпса буде мати вигляд:

Якщо в цьому рівнянні замінити х на 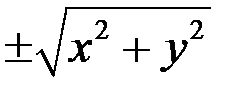, то вийде рівняння

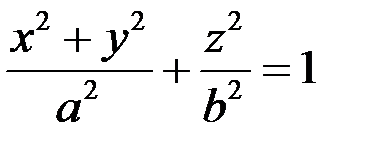
відповідної поверхні обертання. Отже, еліпсоїд обертання з віссю обертання Oz описується рівнянням:

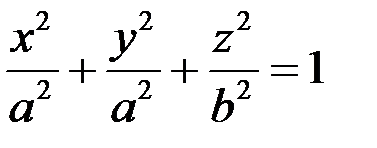. (16.2)

Рис. 16.3. Еліпсоїд обертання Рис. 16.4. Еліпсоїд обертання навколо вісі Oz

Застосуємо до еліпсоїда обертання перетворення стиснення до координатної площини Oxz, отримаємо еліпсоїд загального виду. Якщо k - коефіцієнт стиснення, то рівняння еліпсоїда набуде вигляду:

,

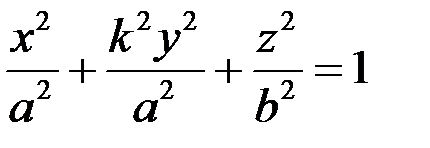або, після заміни :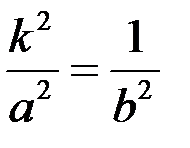

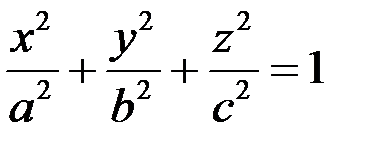. (16.3)

Рівняння (16.3) називають канонічним рівнянням еліпсоїда. Три параметри а, b і c, ― це напівосі еліпсоїда (рис. 16.5). Якщо всі три напівосі еліпсоїда попарно різні, то еліпсоїд називають тривісним.

Рис. 16.5. Тривісний еліпсоїд

Якщо рівні всі три напівосі (а = b = с = r), то еліпсоїд перетворюється в сферу радіуса r, яка описується рівнянням:

.

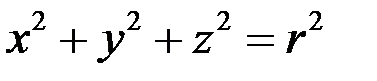16.5. Гіперболоїди

При обертанні гіперболи навколо однієї з її осей симетрії отримаємо поверхню, що називається гіперболоїдом обертання. Вибір осі обертання впливає на тип гіперболоїда. Якщо віссю обертання є дійсна вісь симетрії гіперболи, то поверхня обертання буде складатися з двох частин (порожнин). Це двопорожнинний гіперболоїд обертання (рис. 16.6). При обертанні гіперболи навколо її уявної осі симетрії поверхня буде складатися з однієї порожнини (рис.16.7). Таку поверхню називають однопорожнинним гіперболоїдом обертання.

Для виведення рівнянь гіперболоїдів обертання розташуємо прямокутну систему координат так, щоб вісь обертання, яка є віссю симетрії гіперболи, збігалася з віссю аплікат Оz, а сама гіпербола була розташована в координатній площині Оxz з центром в початку системи координат. Для двопорожнинного гіперболоїда обертання рівняння гіперболи буде мати вигляд:

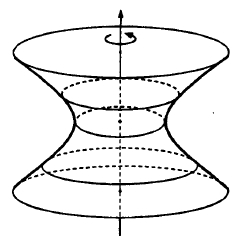
Рис. 16.6. Двопорожнинний гіперболоїд Рис. 16.7. Однопорожнинний гіперболоїд

Замінивши в ньому х на , отримаємо рівняння

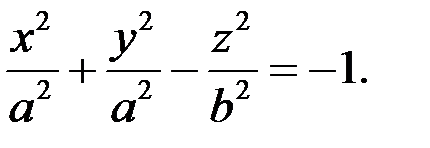(16. 4)

Це рівняння двопорожнинного гіперболоїда обертання.

У випадку однопорожнинного гіперболоїда, гіпербола, що обертається буде мати рівняння:

Знову міняємо х на радикал , отримуємо

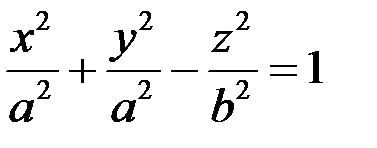. (16.5)

Це рівняння однопорожнинного гіперболоїда обертання.

Гіперболоїди обертання перетворенням стиснення до координатної площини Оxz перетворюються в двопорожнинний і однопорожнинний гіперболоїди загального вигляду. Їх рівняннями будуть відповідно

і

Після заміни 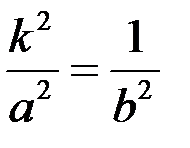отримаємо канонічне рівняння двопорожнинного гіперболоїда (рис. 16.8): , (16.6)

і однопорожнинного (рис. 16.9) гіперболоїда: 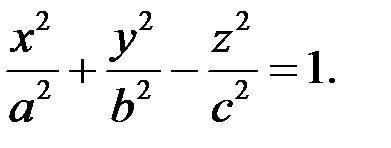(16.7)

З рівнянь (16.6) та (16.7) видно, що обидва гіперболоїди ― поверхні другого порядку.

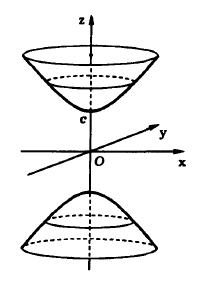
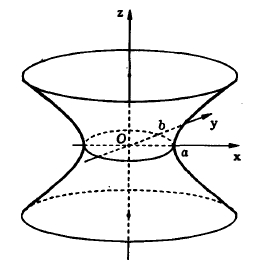
Рис.16.8. Канонічний двопорожнинний Рис. 16.9. Канонічний однопорожнинний

гіперболоїд гіперболоїд

16.6. Еліптичні параболоїди

При обертанні параболи навколо її осі отримуємо параболоїд обертання (рис.16.10). Щоб знайти його рівняння, виберемо прямокутну систему координат, спрямуємо вісь Оz по осі обертання і поєднаємо координатну площину Oxz з площиною параболи. Нехай при цьому парабола описується рівнянням . Тоді для отримання рівняння поверхні обертання потрібно замінити в цьому рівнянні х на :

Перетворення стиснення параболоїда обертання до координатної площини Oxz з коефіцієнтом k дає поверхню більш загального вигляду ― еліптичний параболоїд, рівнянням якого буде

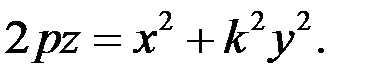
Після заміни 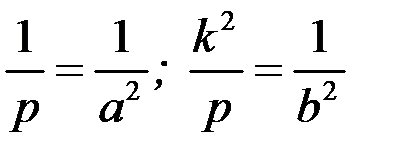параметрів отримаємо канонічне рівняння еліптичного параболоїда:

. (16.8)

Еліптичний параболоїд є поверхнею другого порядку. При a = b він перетворюється в параболоїд обертання.

Рис. 16.10. Параболоїд обертання

Дата добавления: 2014-12-25