Однокритериальные задачи оптимализации

Х Х

Обратные задачи позволяют выбрать такое решение х, при котором критерий оптимизации примет максимальное (минимальное) значение.

Прямые задачи позволяют ответить на вопрос, что произойдет и чему будет равен критерий оптимизации, если принимается решение х Х.

ПРЯМЫЕ И ОБРАТНЫЕ ЗАДАЧИ ОПТИМИЗАЦИИ.

Все задачи в области оптимизации можно разделить на два основных типа: пря­мые и обратные.

Для решения прямых задач необходимо построить математическую модель, которая позволяет рассчитать критерий оптимизации (или несколько параметров) в зависимости от заданных условий.

Из сказанного следует, что решение обратных задач требует, чтобы сначала решена была прямая задача.

Различают одномерные и многомерные задачи оптимизации. В первом случае изменяется лишь один параметр объекта, в то время как другие независимы от него и стабилизированы. Но в практике таких задач сравнительно мало. Более широкую группу составляют задачи многомерной оптимизации, когда одновременно в объекте задействованы несколько параметров.

Рассмотрим постановку задачи оптимизации в общей форме.

Эффективность операции определяется одним или несколькими критериями оптимизации - W.

Если условия операции известны, то все факторы условно можно разделить на две составные группы:

1. Заданные и заранее известные факторы и ограничения - а;

2. Зависящие от нас элементы решения, образующие в своей совокупности решение х (числа, векторы, функции и т. д.).

Тогда можно записать:

W=f(a,x) (1.6)

Если зависимость (1.6) известна, то прямая задача решена. Обратная задача в этом случае записывается в виде:

W* = max(min) [ W(a,x)] (1.7)

где W* - показатель оптимизации, имеющий максимум (минимум).

Решение (1.7) имеет место при х=х*, где. x * - решение, обеспечивающее W*.

Поиск экстремума функции или функционала W- далеко не простая задача.

Если функция W линейно зависит от элементов решения x₁, ,х;, х₃,.. х_n и ограни­чения, налагаемые на них, имеют вид линейных равенств и неравенств, то для этих целей используются методы линейного программирования, которые детально разработаны вплоть до стандартных процедур.

В случае, когда W выпукла (нелинейная), применяются методы выпуклого, чаще всего квадратичного программирования.

Динамическое программирование применяется главным образом для оптимиза­ции управления многоэтапными операциями.

Однако критерий оптимизации зависит также еще от одной группы факторов, гак называемых неизвестных факторов, которую обозначим через "b" и которые формируют условия неопределенности. В этом случае:

W=f(a;x;b)(1.8)

Задача поиска оптимального решения в этих условиях приобретает неопределенность. От исследователя требуется найти такое решение в условиях неопределенности, которое обеспечит оптимальное значение критерия оптимизации.

КРИТЕРИИ ОПТИМИЗАЦИИ

Критерий оптимизации является характеристикой цели и определяет признак, по которому оптимизируется процесс.

Под критерием оптимизации также понимается математический эквивалент цели управления, являющийся функционалом, который зависит от факторов и показателей процесса.

К критерию оптимизации предъявляется ряд требований. Он должен:

• иметь ясный физический смысл;

• однозначно характеризовать объект исследования;

• технологически легко измеряться и выражаться количественно;

• с достаточной полнотой и универсальностью описывать объект.

Если оптимизация осуществляется по одному какому-либо критерию, то такие критерии называются частными, а задачи - однокритериальными.

Значения критерия оптимизации могут быть дискретными и непрерывными.

На критерий оптимизации накладываются различные ограничения (упоры). Ши­роко используются так называемые директивные ограничения. Примером таких ог­раничений могут быть:

■ минимальный выход керна, определяемый из условий достоверности геологического опробования;

■ минимальные скорости и производительность бурения, определяемыми плановыми показателями разведки или добычи;

■максимальная затрачиваемая мощность, ограниченная параметрами привода.

Производительность бурения оценивается скоростями бурения. Механическая скорость бурения :

,

где 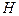- углубление скважины, м; 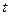- текущее время чистого бурения, с.

В общем виде можно записать

,

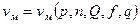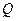где - осевая нагрузки на породоразрушающий инструмент; - частота вращения; - расход очистного агента; 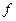- свойства горных пород, влияющие на буримость; 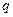- степень износа породоразрушающего инструмента.

Дата добавления: 2014-12-25