Л.С. ВЫГОТСКИЙ 3 страница

Ені a=MN ұзын саңлауда болатын Фраунгофер дифракциясын қарастырайық.. MC және ND шоқтарының арасындағы жүру жолдарының оптикалық айырмашылығы:

∆= NF sin aφ. MN толқындық бетті Френель зоналарына бөлейік. Әр зонаның еніне ∆: λ/2 зона сәйкес келеді. Толқындық фронттың әр нүктесінің фазасы және амплитудасы біркелкі. Сондықтан көршілес Френель зоналарының тербеліс қарқындылығы нольге тең болады. Яғни:1) егер, Френель зоналарының саны тақ болса,онда: 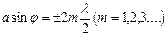дифракциялық минимум шарты

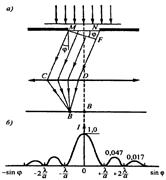2) егер, Френель зоналарының саны жұп болса, онда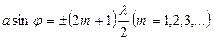

дифракциялық максимум шарты

Дифракциялық тордағы Фраунгофер дифракциясы.

Бір саңылаудан пайда болатын дифракцияны қарастырғанда ақ және қараңғы жолақтар бірінен кейін бірі орналасқанын

3.4-сурет

байқадық. Енді жарық сәулелерін бір саңылаудан ғана өткізбей, осындай бірнеше саңылаудан өткізсек, онда пайда болған ақ және қара жолақтардың ені бір саңылаудан өткен жолақтардың еніне қарағанда енсіздеу (аздау) және жарығырақ болатыны байқалған. Осы жолақтарды дифракциялық бейне деп атайды. Ондай бейнелерді алу үшін дифракциялық тор пайдаланылады. Дифракциялық тор деп параллель орналасқан ені бірдей саңылаулар жиынтығын айтамыз. Дифракциялық тор әдетте шыны пластинканың бетіне сызат жасау арқылы алынады. 1мм шыны пластинкаға 1200-ге дейін сызат салынады. Егер жарық өткізбейтін бөліктің енін b, ал өткізетін бөліктің енін a десек, онда d=a+b – тор периоды деп аталады. Тор периоды мен жарықтың толқын ұзындығының арасында мынадай байланыс бар: 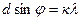, мұндағы к=0, ±1, ±2...- спектр реті.

Дифракциялық тор күрделі жарықты спектрлерге жіктей алады. Сондықтан дифракциялық тор жарық құрамын зерттеу үшін пайдаланылатын құралдардың негізгі бөлігі болып саналады. Ол құралдарды торлы спектрлік құралдар немесе дифракциялық спектроскоп деп атайды.

Бір және көп саңылаулардағы дифракция.
Дифракциялық тор

Саңылаудағы Фраунгофер дифракциясы үшін экранда ин­тен­сивтіліктің таралуы дифракцияланатын шоқтардың ба­ғы­ты­мен анықталады. Саңылауды өзіне параллель ығыстырғанда диф­ракциялақ бейне өзгермейді. Сондықтан екі саңылаудың әр­қайсысы жеке құрған дифракциялық бейне бірдей болады. Қо­рытынды бейне екі (3.16 сурет) саңылаудан келген тол­қын­дар­дың интерференциясымен анықталады.

Ендері а, өзара b (a+b=d) арақашықтықта орналасқан екі са­ңылау мөлдір емес экранда орналасқан. Жазық монохромат жа­рық толқыны экранға қалыпты түседі. Минимумдар бір са­ңы­лаудағы сияқты сол орнында табылады. Яғни бұрынғы бас ми­нимумдар келесі шартпен анықталады.

3.16-cурет

A sinφ=±mλ (m=1,2,3,…). (1)

Екі саңылаудан шықан жарық шоқтарының өзара ин­тер­фе­ренциялану нәтижесінде кейбір бағыттарда олар бірін-бірі өші­реді, яғни қосымша минимумдар пайда болады. Бұл бағыт екі саңылаудың нүктелерінен (М және С нүктелерінен) келген шоқ­тардың λ/2, 3λ/2,... жол айырымына сәйкес келеді. 3.16 –су­ретте көрсетілгендей бұл бағыттар келесі шартпен анық­та­ла­ды:

CF=MC sinφ=(a+b)sinφ=d sinφ=λ/2, 3λ/2,…. (2)

(2) теңдеуді ескере отырып, қосымша минимумдар шар­ты:

d sinφ=±(2m+1)λ/2 (m=0,1,2,…) (3)

келесі бағыттарда: d sinφ=±2mλ/2=±mλ (m=0,1,2,…) (4)

бір саңылаудың әсері екінші саңылаудың әсерін күшейте тү­се­ді, сондықтан осы бағыттар бас максимумдарды береді.

Сонымен екі саңылаудағы дифракциялық бейне келесі шарт­пен анықталады

Бас минимумдар a sinφ= λ, 2λ, 3λ, …

Қо­сымша минимумдар d sinφ= λ/2, 3/2λ, 5/2λ, …

Бас максимумдар d sinφ=0, λ, 2λ, 3λ, …,

Яғни екі бас максимумдар арасында қосымша минимум ор­наласады, ал максимумдар бір саңылау жағдайынан гөрі жіңішкерек болады.

Аналогия бойынша саңылау саны N болғанда, қосымша ми­нимумдар саны (N –1)-ге тең болады. Бір жазықтықта жат­қан және мөлдір емес аралықтармен бөлінген ендері тең па­рал­лель саңылаулар жүйесін бір өлшемді дифракциялық тор деп атайды. Саңылау мен оның мөлдір емес аралықтарының а жә­не b ендерінің қосындысы (d=a+b) дифракциялық тор­дың тұрақтысы деп аталады. Тордағы дифракция бейнесі са­ңы­лаулардан келген толқындардың өзара интерференциясы нә­тижесімен анықталады. Д ифракциялық тордағы жарық диф­ракциясының бас минимумдары келесі шартқа сәйкес ке­ле­ді:

a sinφ =± m λ (m =1,2,3,…), (5)

Басі максимумдары келесі шартқа сәйкес келеді:

d sinφ =± n λ (n =1,2,3,…),(6)

мұндағы n – бас максимумдар реті. Егер φ –дің кейбір мән­дері бірдей мезгілде (5) және (6) шарттарын қа­на­ғат­тан­дыр­са, онда бұл бағыттарда бас максимумдар бақыланбайды.

Мысалы, а=d/3-те әр үшінші бас максимум ба­қы­лан­бай­ды.

Әрбір екі бас максимумдар арасында келесі шартқа сәйкес ке­летін (N –1) қосымша минимумдар орналасады:

d sinφ =± m' λ/N (m'≠0, N, 2N, …), (7)

яғни, m ' – (7) шарттың (6)-ға ауысатындығынан тыс бү­тін сандардың мәндерін алады. Сонымен қатар, (N-2) қо­сым­ша максимумдарды да көруге болады. Олардың ин­тен­сив­ті­лік­те­рі бас максимумдермен салыстырғанда өте аз (<5%) бол­ған­дық­тан оларды аңғару қиынға түседі.

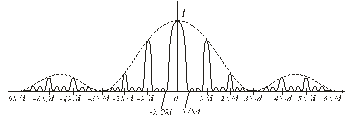
3.17-сурет

Мысал ретінде 3.17 суретте N=4 және d/a= 3 теңге сәйкес диф­ракциялық бейне берілген.

Егер жарықтың параллель сәулелері дифракциялық торға көл­беу түссе (3.18-сурет) шоқтардың жол айырымы:

CB-AD=d sinφ₀ –d sinφ = d(sinφ₀ –sinφ),

мұндағы φ₀ –дифракциялық тор бетіне жарық шоғының тү­су бұрышы. Егер d(sinφ₀ –sinφ) толқын ұзындықтарының бү­тін санына тең болса, онда максимумдар байқалады.

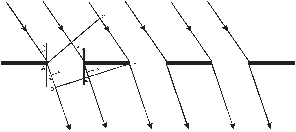
3.18-сурет

3.

1.Спектрлік анализ. Әрбір затты (яғни химиялық элементті) қатты қыздырғанда немесе газға айналдырғанда онан шашырап бөлінетін сәуленің түстері (спектрі) сол заттың ішкі құрылысына байланысты болады. Демек, осыған сүйеніп минералдар түйіршіктерін қыздырып, онан шыққан спектрді зерттеу арқылы оның ішінде қандай элемент бар екенін айыруға болады. Спектрлік анализ деп осыны айтады. Спектрлік сәуленің қанықтығына қарай элементтердің мөлшерін де ажыратады. Сондықтан бұл әдіс — өте қолайлы әдіс. Өйткені минералдың кішкентай белшек ұнтағынан қандай элемент қанша мөлшерде екенін тез және оп-оңай айыруға болады.

Голография – 1948 ж. ағылшын физигі Д. Габор ойлап тапқан әдіс. Әдістің мәнісі толқындарды алдымен арнайы жазықтыққа тіркеп, кейін қалпына келтіру жолымен объектінің көлемдік бейнесін алу. 1963 жылы американдық Э.Лейт пен Ю.Упатниекс алғаш рет лазерлік голограмманы алды

2.Ферми деңгейі — жартылай бүтін спины 6aр бөлшектер (фермиондар) жүйесінің абсолют нөл температурада бос және толтырылған энергетикалық деңгейлерін бөліп тұратын энергияның мәні SF (Ферми энергиясы). Фл түсінігі шалаөткізгіштердің өткізгіштігін түсіндіретін аймақтық теориялар қолданылады.

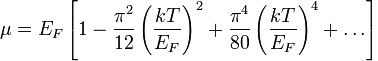
Ферми беті - абсолют нөл кезінде электрондардың температура болмайтын облыстан, металдардың бос емес электрондық күйінің облысын бөлектейтін квазиимпульстар кеңістігіндегі энергияға тең бет.

Жарықтың затта таралуы.Дисперсия.Жарықтың жұтылуы. Зоналық теория тұрғысынан металдар диэлектриктер жартылай өткізгіштер

Жарық – ерекше серпімді ортада таралатын толқындық процесс. (1678ж Гюйгенс тұжырымдаған)Бұл пікір бойынша жарық та дыбысқа ұқсас сфералық беттер және толқындар түрінде таралады.Сонда жарық толқындары эфирде таралатын механикалық серпімді тербелістер б.т.

Дисперсия (лат. dispersion - шашырау).

Ньютон ашқан құбылысы жарықтың жарықтың дисперсиясы деген атқа ие болды. Жарық дисперсиясының екі мағынасы бар:

1)дисперсия – күрделі ақ түсті спектрге ажырату.

2)дисперсия – заттың абс. сыну көрсеткішінің затқа түсетін жарықтың жиілігіне тәуелділігі.

n = f( 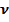) = 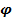( 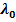) 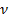– жиілік

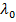– толқын ұзындығы

Дисперсия тек монохромат емес толқындар таралғанда ғана байқалады.

Толқын ұзындығы төмендегенде сыну көрсеткіші артады. Бұл қалыпты дисперсия д.а.(нормаль)

Егер толқын ұзындығы артқанда, сыну көрсеткіші де артатын болса, онда ол қалыпсыз дисперсия д.а.

Жарық зат арқылы өткенде жарық толқының энергиясының жоғалуы жұтылу д.а.

I =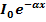

I – заттан шығатын жарықтың интенсивтілігі

жұтылу коэффиценті

Жұтылу коэффиценті жарықтың интенсивтілігіне байл. емес ол тек жарық толқынының ұзындығына байланысты және әр түрлі заттар үшін әр түрлі мән қабылдайды.

Егер Х= болса, онда жарықтың интенсивтілігі (е) есе кемиді. (е = 2.73)

Жұтылудың сызықтық спектрлерін бір атомды газдар және металдар буы береді. ( = )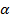

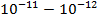Молекулалардың жұтылу спектрлері атомдардың және молекулалардың тербелісімен анықталады. = )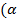

Жұтылудың тұтас спектрлерін диэлектрлерде байқалады. Диэлектриктерде еркін электрондар жоқ. ( =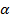

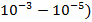
Зоналық теорияда көп электронды есеп бір электронның қозғалысына келтіріледі. Атомдар оңашаланған кезде бір бірінен макроскопиялық қашықтықта болған кездегі олардың энергетикалық деңгейлеріне сәйкес келеді. Ал криссталдық торда атомдар арасындағы қашықтық қатты денедегі атомдар арасында болғанда, атомдардың энергетикалық деңгейлері ығысады. Зоналар ұлғаяды, нәтижесінде зоналық энергетикалық спектр түзіледі. Ішкі қабаттағы электрондар оңашаланған атомдар сияқты болса, сыртқы қабаттағы электрондар бүкіл қатты дене бойында таралады.

Егер валентті электрондар ядромен нашар байланыс түзсе, онда рұқсат етілген зоналар кең болады. Зоналар рұқсат етілген, рұқсат етілмеген болып бөлінеді.

Валенттік зона электрондармен толықтырылған. Атомдардың ішкі энегетикалық деңгейлеріндегі электрондардан түзіледі. Зоналық теория тұрғысынан температураның жоғарылауымен валенттік зонаның жоғарғы деңгейінде орналасқан электрондар өткізгіштік зонаның төменгі деңгейіне өтеді. Бұл жағдай да өткізгіштер электронмен жүргізіледі. Электронның қозғалысымен жасалатын өткізгіштік n-типті д.а. кемтіктер электронның қозғалыс бағытына қарсы қозғалады. Өткізкіштік кемтіктік немесе р-типті д.а. меншікті жартылай өткізгіштің өткізгіштігі жартылай электронмен, жартылай кемтіктермен жасалады.

3.

Денеден шығатын жарық толқындары сол денені құрайтын жекелеген атомдардың шығарып жатқан электромагниттік толқындарының қосындысынан тұрады. Осы электромагниттік толқындардың ішінен біреуін таңдап алып, оны екі перпендикуляр вектордың тербелісі деп қарастыруға болады. Оның біреуі электр өрісі кернеулігінің векторы Е, екіншісі магнит өрісі кернеулігінің векторы Н. Бұл екі вектордың тербеліс жазықтықтары сәуленің таралу бағытына перпендикуляр орналасады. Ал атомдар электромагниттік толқындарды біріне-бірі байланыссыз шығара береді. Сондықтан олардың тербеліс жазықтықтары әр түрлі бағытта болады, басқаша айтқанда жарық векторының тербеліс жазықтығы өз бағытын үнемі өзгертіп отырады. Осы электромагниттік тербелістер жарық көзінен шығып бізге қарай бағытталсын. Сонда әрбір атомнан шыққан электромагниттік толқындар а-суреттегідей бейнеленеді. Жарық векторы кеңістікте осылайша түрлі бағытта орналасса, ондай жарықты табиғи немесе поляризацияланбаған жарық деп атайды. Белгілі бір жағдайда, мысалы, жарық кристалл арқылы өткенде табиғи жарық шоғының ішінен Е векторы тек бір ғана жазықтықта тербелетін сәулені бөліп алуға болады. Оны толық поляризацияланған жарық деп атайды. Бұл б – суретте көрсетілген. Е векторы тербелетін жазықтыққа параллель жазықтықты поляризация жазықтығы деп атайды.

Кемтіктердің концентрациясы электрондардың концентрациясынан артық болатын өткізгіштер кемтіктік немесе р-типті жартылай өткізгіштер деп аталады.

ЖАРТЫЛАЙ ӨТКІЗГІШТЕРДІҢ ТҮРЛЕРІ

Жартылай өткізгіштерде Менделеев кестесінің орта тұсындағы он екі химиялық элементтер жатады. Олар: бор (В), көміртегі (С), кремний (Si), германий (Ge), қалайы (Sn), фосфор (Р), мышьяк (As), сурьма (Sb), күкірт (S), селен (Se), телмур (Те), йод (І). Ғылым мен техникада ең көп қолданылатын жартылай өткізгіштерге германий Ge және кремний Sі жатады.

Жартылай өткізгіштер өзіндік (яғни қоспасыз) және қоспалы болып бөлінеді.

Өзіндік жартылай өткізгіштердің электр өткізгіштігі

Өзіндік жартылай өткізгіштердің электр өткізгіштік механизмін германийдің немесе кремнийдің монокристалының мысалында қарастыру қолайлы.Себебі өте кең қолданылатын жартылай өткізгіштер Ge және Sі сыртқы электрондық қабатта төрт электроны болады, яғни олардың валенттілігі төртке тең. Мұндай элементтердің кристалдық торында (алмаз типті тор деп аталынатын) германийдің Ge немесе кремнийдің Sі әрбір атомы, бірдей қашықтықта орналасқан, көрші төрт атоммен қоршалған.

Атомның ең орнықты күйі, оның сыртқы электрондық қабатында сегіз электрог тұрған кезде екендігі белгілі. Сондықтан Ge және Sі атомдары электрондық қабаттарды сегіз электронға дейін толтырып, көрші атомдармен жалпы электрондық жұп құрайды (коваленттік байланыс).

Әрбір екі көрші атомдар екі ортақ электрондары (электрондық жұп) болады. Сонымен, әрбір атом сыртқы қабатында сегіз электроннан болады, олар бір мезгілде көрші атомдарға да жатады. Алмаз типті торды шартты түрде жазық етіп бейнелеуге болады, өйткені мұнда да әрбір атом көрші төрт атоммен қоршалған. Төменгі температурада жартылай өткізгіштің кристалында барлық электрондар атомдармен байланысқан және еркін электрондары жоқ, яғни кристалл диэлектрик болып саналады. Жартылай өткізгіштің температурасын көтерген кезде кейбір электрондар атомнан бөлініп, жылжымалы күйге түсіп, оған кернеу түсіргенде, кристалда ток жасайды.

Атомнан электронды бөліп шығарған кезде атомның қабатшасында бос орын пайда болады, ол орынды «кемтік» деп атайды. Ортақ электрондары бар көрші атомдар, электрондармен үнемі алмасып тұратындықтан, бұл кемтік басқа электронмен толтырылуы мүмкін және бұл кезде енді басқа атомда бір электрон жетпей тұрады. Электрон үзіліп шыққанға дейін атом электрлік нейтраль болғандықтан, онда электронның жетіспеуі атомға оң заряд береді. Сондықтан, электронның бос орны – кемтіктің зарядын оң деп санайды. Бұл бос орын – кемтік – кристалл көлемінде үнемі және тынымсыз орын ауыстыруда болады, бұл заряды сандық жағынан электрон зарядына тең оң зарядтық осылай ауысып отырумен бірдей болады.

Сонымен, бос электрондар және кемтіктер кристалл бойынша, қандай да бір еркін электрон атом қабатшасындағы кемтікпен кездескенше, ретсіз орын ауысып отырады (бос орынға тап болғанша). Бұл кезде қозғалыстағы екі зарядты тасымалдаушылар жоқ болады: бос электрон және кемтік, яғни рекомбинация жүреді.

Әрбір белгілі-бір температурада жұптың пайда болуының «электрон-кемтік» (генерация) және олардың жойылуының (рекомбинация) аралығында динамикалық тепе-теңдік орнайды. Неғұрлым температура жоғары болған сайын, солғұрлым «электрон – кемтік» жұптары пайда болып, жартылай өткізгіш кристалында олардың бір мезгілде болуының саны артады.

Қоспалы жартылай өткізгіштердің өткізгіштігі

Егер балқытылған таза германийге немесе кремнийге Менделеев кестесіндегі үшінші топтың элементтерінің атомдарының (Іn, Al, Ga, B және басқалар) аздаған мөлшерде қосса, мысалы Іn, онда қатайғаннан кейін Іn атомдары кристалдық тордың кейбір түйіндерінен орын алып, кристалдық құрамына енеді. In атомдары кристалда төрт көрші Ge атомдарымен ортақ электрондық жұп құрайды. Алайда индий Іn атомында сыртқы электрондық қабатта үш қана электрон болғандықтан, сегіз электроннан тұратын орнықты қабат құру үшін, оған бір ортақ электрон жетіспейді. Іn атомы жетіспейтін электронды көрші германийдің Ge атомынан қамтып алуы мүмкін. Сонда ол теріс зарядталады да, ал қандай да бір орында жылжымалы кемтік пайда болады.

Кристалл электронейтраль болып қала береді, бірақ ондағы теріс зарядталған In атомдары тормен байланысқан (локалданылған), ал оң зарядталған кемтіктер электр тогына қатысуы мүмкін. Мұндай

кристалдың өткізгіштігі негізінен кемтік болады, өйткені кристалда пайда болған кемтіктердің саны, аздаған қоспаны ендіргеннің өзінде (10^-4 – 10^-6 %), қоспасыз жартылай өткізгіштегі «электрон-кемтік» жұбының санынан едәуір көп болады.

Егер жартылай өткізгіште атомдары электрондарды қамтып алатын, Менделеев кестесіндегі ІІ топтағы элементтердің қоспасы болса, онда мұндай қоспаны р-типті қоспа деп атайды («позитив» - оң деген сөз) немесе акцепторлық (аламан) қоспа, ал кристалл р-типті жартылай өткізгіш деп аталынады.

р- типті жартылай өткізгіштерде негізгі электр өткізгіштіктің рөлін – жылжымалы зарядтардың негізгі тасымалдаушылары – кемтіктер атқарады.

Германий торына Менделеев кестесінің V тобының атомдарын ендірсе (As, Sв, Р және басқалар), мысалы мышьякты Аs, сыртқы қабатшадағы төрт электрон (қоспа атомының сыртқы қабатшасындағы бес электрондардың төртеуі) көрші төрт германий Ge атомдарымен ортақ электрондық жұптар құрады, және де әрбір атомда, соның ішінде мышьяк As атомында да, ортақ электрондардың арқасында сыртқы электрондық қабат орнықты болатын санға жетеді (сегіз электрон). Мышьяк As атомының бесінші сыртқы электроны «артық» болып қалады. Ол, басқа электрондарға қарағанда ядромен нашарырақ байланысқан, және де оны аздаған энергия шығындап, атомнан бөліп бос электронға айналдыруға болады. Бұл кезде мышьяк As атомы оң зарядталады (иондалады).

Сонымен, германий кристалының торына V топтың атомдарын ендірген кезде тордың түйіндерінде оң зарядталған «қозғалмайтын» қоспаның иондары және еркін электрондар пайда болады. Мұндай жартылай өткізгіштердің өткізгіштігі негізінен электрондық болады. Бұл жағдайда

кристалды n-типті жартылай өткізгіш деп атайды («негатив» - теріс деген сөз), ал қоспаны n-типті қоспа немесе донорлық (беремен) деп атайды.

3.

1. Абсолют қара дененің сәулеленуі. Планктың кванттық гипотезасы және формуласы.

Өзіне түскен сәулелерді толқын ұзындығына байланыссыз толығымен жұтатын денені абсолют қара дене деп атайды. Абсолют қара дененің жұту коэффициенті бірге тең: .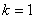

Жұту коэффициенті бірден кіші дене абсолют қара емес дене немесе қоңыр дене деп аталады: .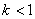

Абсолют қара дененің спектрлік сәуле шығарғыштық қабілеті 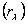толқын ұзындығы мен температураға тәуелді болады:

.

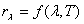Неміс ғалымы Кирхгоф дененің сәуле шығарғыштық қабілетінің 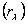сәуле жұтқыштық қабілетіне 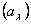қатынасы дененің табиғатына тәуелсіз, барлық денелер үшін бірдей, сәуленің толқын ұзындығы мен температураға тәуелді универсал функция болады деген қорытынды жасады, яғни:

,

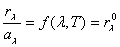мұндағы: - температурасы дене температурасымен бірдей абсолют қара дененің сәуле шығарғыштық қабілеті.

Дата добавления: 2014-12-25