Приклад 1.3. В якості прикладу визначимо запас міцності консольної конструкції з прямолінійних стержнів прямокутного профілю

В якості прикладу визначимо запас міцності консольної конструкції з прямолінійних стержнів прямокутного профілю, які жорстко з’єднані у вузлах (рис. 1.22). Навантаження мають значення 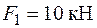, , 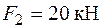, 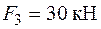а довжини ділянок 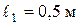, , 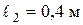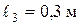. Розміри прямокутного профілю у кореневому перерізі О-О дорівнюють 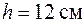, 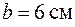. Причому сторони позначають, щоб виконувалась нерівність 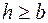. Припустимо, що матеріал конструкції має межу текучості .

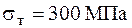При побудові епюр внутрішніх силових факторів для нашої конструкції (рис. 1.22) у даному прикладі використаємо принцип суперпозиції. Сили 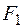, , , 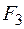будемо прикладати послідовно, відстежуючи дію кожної сили окремо на всіх ділянках просторового бруса. Загальний результат отримаємо, якщо просумуємо відповідні епюри на усіх ділянках конструкції.

Спочатку будемо вважати, що діє лише сила 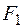. Схема ї приведення до різних вузлів конструкції наведена на рис. 1.24.

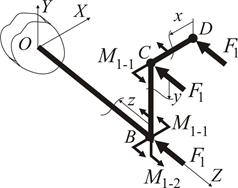
Рисунок 1.24

Паралельний перенос 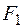з D до С породжує момент у площині .

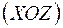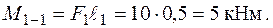
Рух сили з С до В утворює додатковий момент у площині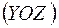

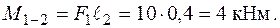
Таким чином (рис. 1.24), перша ділянка DС знаходиться в умовах поперечного згинання в площині .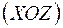

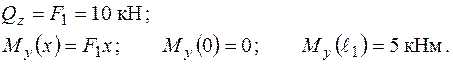
При погляді з додатного напрямку осі „ у ”, стислими на цій ділянці є волокна стержня, що зліва (які мають від’ємну координату „ z ”).

На другій ділянці СВ маємо сумісну дію поперечного згинання в площині 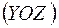та кручення

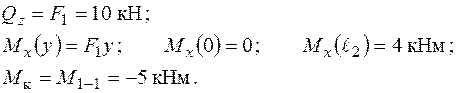
Епюра моменту 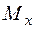повинна бути розташована на правих, стислих волокнах ділянки, при погляді з додатного напрямку осі „ х ”.

Третя ділянка ОВ стискається поздовжньою силою

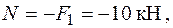
а також згинається постійними сконцентрованими моментами у двох головних площинах перерізу

Момент 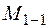, площина дії якого 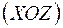стискає праві волокна стержня ОВ (з додатною координатою „ х ”). Момент 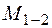діє у площині 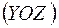, стискаючи верхні волокна ділянки (волокна, що мають додатну координату „ у ”).

Розподіл вказаних силових факторів зображений на рис. 1.25.

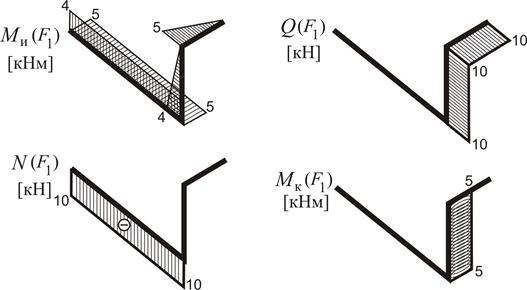
Рисунок 1.25

Слід зауважити, що всі вузли конструкції „ n ” повинні відповідати умовам рівноваги під дією внутрішніх моментів в однієї площині, тобто виконується рівняння:

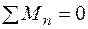
На рис. 1.26 показані внутрішні моменти, що діють при наближенні до вузла С з боку першої та другої ділянки

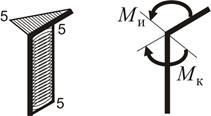
Рисунок 1.26

Такий спосіб контролю при побудові епюр слід застосовувати до кожного вузла конструкції.

Розглянемо опір конструкції під дією сили (рис. 1.27).

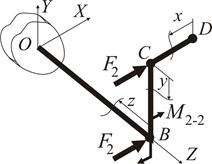
Рисунок 1.27

Дія сили розповсюджується на другу та третю ділянки конструкції. Згідно з прийнятим порядком розгляду інтервалів (рис. 1.23), до першої ділянки вона не потрапляє.

Тож зусилля дає поперечне згинання другої ділянки

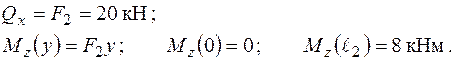
Площина дії моменту – , стислі волокна стержня у цій площині – праві, з додатною координатою „ х ”. У точці В момент 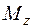набуває значення

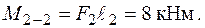
Такий момент є крутним по відношенню до ділянки ВО, вісь якої ортогональна до площини його дії. Зусилля у точці В стає поперечним до останньої ділянки (рис. 1.27), тому воно згинає стержень ОВ у площині 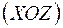. Стислі волокна у цій площині мають додатну координату „ х ”.

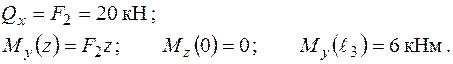
Епюри силових факторів від дії навантаження зображені на рис. 1.28.

Рисунок 1.28

Зона дії зусилля 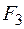обмежується лише третьою ділянкою ОВ (рис. 1.29).

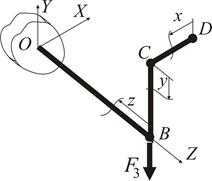
Рисунок 1.29

Сила 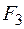вже приведена до початкової точки останнього інтервалу та є поперечною до нього, тому

Площина дії моменту 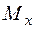– 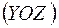, стислі волокна розташовані знизу і мають від’ємну координату „ у ”. Епюри внутрішніх силових факторів від дії зусилля 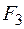наведені на рис. 1.30.

Рисунок 1.30

Якщо просумувати відповідні епюри з рис. 1.25, 1.28, 1.30, отримаємо загальний розподіл внутрішніх сил та моментів по елементах конструкції (рис. 1.31). Сумування проводиться по кожній ділянці з дотриманням знаків та площин розташування часткових епюр.

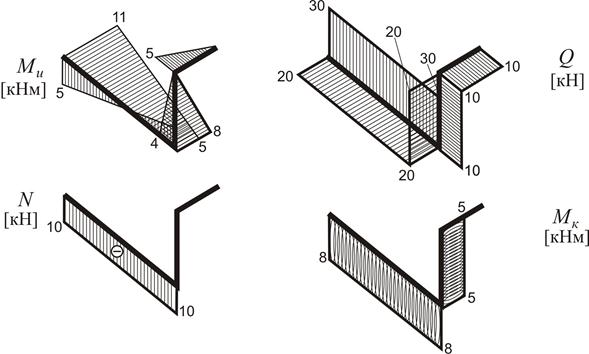
Рисунок 1.31

Значення внутрішніх сил та моментів на сумарних епюрах (рис. 1.31) в перерізі О відповідає реактивним зусиллям 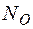, , 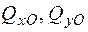, 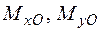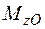у затисненні.

Для того, щоб зробити оцінку щодо несучої спроможності конструкції, треба визначити запас її міцності 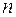по найбільш напруженій точці небезпечного перерізу

,

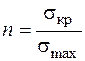де 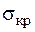– критичне напруження, по відношенню до якого встановлюється запас міцності (це може бути або границя текучості − 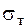, або границя міцності − 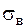), 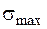– максимальне еквівалентне напруження в небезпечній точці перерізу.

Розглянемо методику визначення коефіцієнту запасу 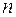. У якості прикладу зупинимося на перерізі О (рис. 1.29), в якому діють усі без виключення внутрішні зусилля (рис.1.31). На рис. 1.32 зображено цей переріз з усіма внутрішніми силовими факторами, дивлячись у бік затиснення.

Напрямок дії внутрішніх зусиль та моментів в перерізі О відповідає напрямкам відповідних реактивних зусиль.

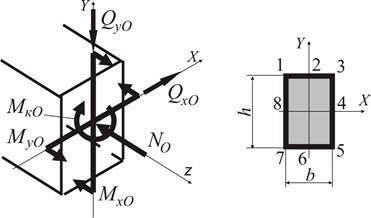
Рисунок 1.32

Підрахуємо напруження від кожного з компонентів внутрішніх зусиль. Для цього знадобляться такі геометричні характеристики перерізу:

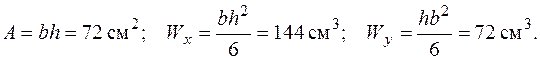
При крученні стержня прямокутного перерізу коефіцієнти 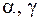визначимо по таблиці [4]. При відношенні сторін прямокутника 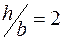, добираємо: .

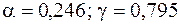Тоді момент опору кручення .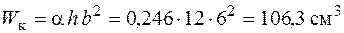

Нормальні напруження від поздовжньої сили 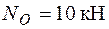рівномірно розподіляються по точках перерізу:

.

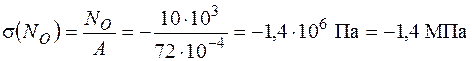Від дії згинальних моментів 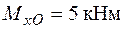, 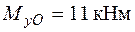нормальні напруження розподіляються за лінійним законом, збільшуючись від нейтральної лінії в обидва боки зі зростанням відповідної координати, так що

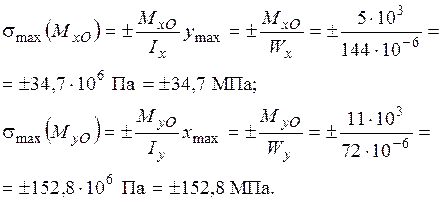
Згідно з напрямком дії, згинальний момент 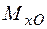(рис. 1.32) розтягує точки І-го та ІІ-го квадрантів і стискає нижню половину перерізу (ІІІ та ІV квадранти). Момент 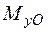(рис. 1.32) діє таким чином, що ліва частина перерізу (ІІ та ІІІ квадранти), опиняється у зоні розтягання, а права частина (І та ІV квадрант) – у зоні стискання.

Дотичні напруження від крутного моменту 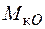набувають максимальних значень у точках, що лежать на серединах сторін прямокутника. Найбільші з них 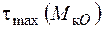з’являються посередині більших сторін. У серединах коротших сторін прямокутника мають місце локальні максимуми напружень :

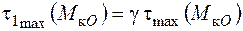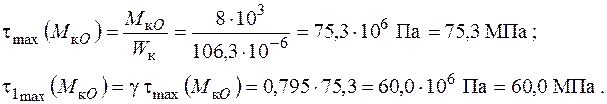
Напруження від дії поперечних зусиль 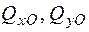теж є дотичними. Вони обчислюються згідно з формулою Журавського і набувають максимальних значень на осях симетрії прямокутного перерізу

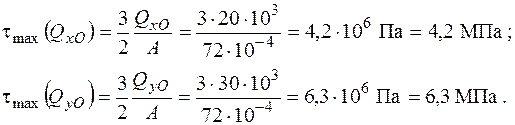
Розподілення компонент напружень в [МПа] в перерізі О–О представлене на рис. 1.33.

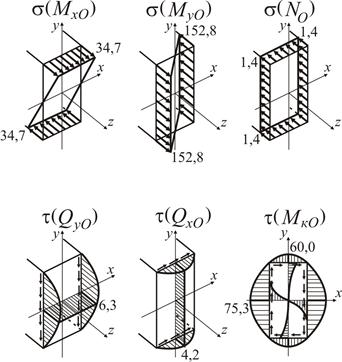
Рисунок 1.33

Дотичні напруження, за напрямком дії, завжди співпадають з відповідним внутрішнім зусиллям. Так, напруження 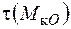у площині перерізу утворюють потік, направлений за годинниковою стрілкою, за напрямком дії 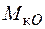. Вектор дії дотичних напружень від дії поперечних зусиль співпадає з вектором самих зусиль.

Аналізуючи напружений стан перерізу можна зробити наступні висновки:

- у кутових точках прямокутника відсутні дотичні напруження, тому ці точки мають лінійний (одновісний) напружений стан;

- найбільш небезпечною точкою перерізу може бути або кутова точка, або точка, що належить до середини сторони прямокутника. Остання має плоский (двовісний) напружений стан, завдяки наявності напружень двох різних типів.

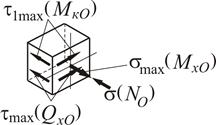
За цими ознаками для аналізу міцності конструкції в небезпечному перерізі оберемо найбільш напружену кутову точку 5, середини більшої (т.4 та т.8) та меншої (т.2 та т.6) сторін прямокутника (рис. 1.32).

В точці 5 діють однакові за знаком нормальні напруження (рис. 1.33, 1.34)

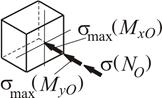
Рисунок 1.34

Напружений стан в точці 5 – лінійний (одновісний), тому сумарне напруження визначається як алгебраїчна сума компонент напружень:

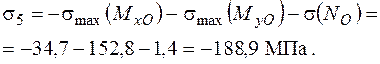
Однозначно визначити найбільш небезпечну точку з номерами 2, 4, 6, 8, неможливо, тому що в точці 4 нормальні і дотичні напруження одного знаку. В точці 8 навпаки, нормальні і дотичні напруження різного знаку. Розглянемо обидві точки. Для точки 4 маємо

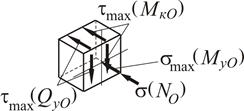
Напружений стан в точці 4 – двовісний (плоский).

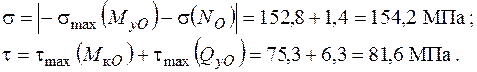
Використовуючи ІV гіпотезу міцності, отримаємо

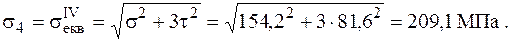
Для точки 8 маємо

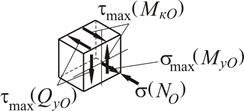
Напружений стан в точці 8 – двовісний (плоский).

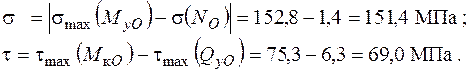
Використовуючи ІV гіпотезу міцності, отримаємо

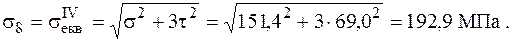
Порівняння напружень у середніх точках коротких сторін прямокутника (рис. 1.33) не дає перевагу жодній точці. Тому розглянемо обидві.

Для точки 6 маємо

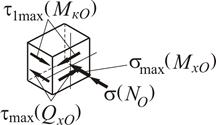
Напружений стан в точці 6 – двовісний (плоский).

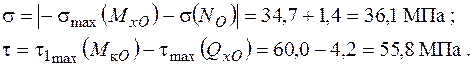
Використовуючи ІV гіпотезу міцності, отримаємо

Для точки 2 маємо

Напружений стан в точці 2 – двовісний (плоский).

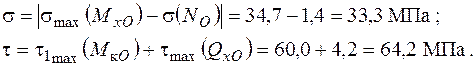
Використовуючи ІV гіпотезу міцності, отримаємо

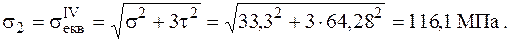
Таким чином, максимальне еквівалентне напруження діє у точці 4, тому коефіцієнт запасу просторового стержня дорівнює:

.

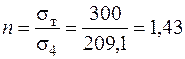Коефіцієнт запасу n > 1. Таким чином можна стверджувати, що умова міцності виконується, а просторовий брус є міцним.

Дата добавления: 2014-12-26