Единиц измерения

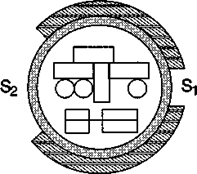
Постановка задачи. Теплоизолированный космический аппарат, находящийся на орбите Земли, имеет на борту приборы с электрической мощностью, которая может изменяться в ходе работы от N₁ = 75 Вт (дежурный режим) до N₂ = 200 Вт (сеанс связи). С целью обеспечения предсказуемого теплового режима в теплоизоляции сделано отверстие площадью S₁, на которое попадает поток солнечной энергии W = 1400 Вт/м². Полученная энергия излучается аппаратом через это и дополнительное отверстие в теплоизоляции с площадью S₂ в режиме «черного тела». Каковы должны быть площади отверстий, если допустимый диапазон температур для оборудования, расположенного в аппарате, составляет 20-30°С?

Анализ задачи. Минимальная температура аппаратуры соответствует режиму минимального тепловыделения. В этом случае поступающая мощность Q_l = WS₁ + N₁. Излучаемая мощность Q₂ = sT⁴₁ (S₁ + S₂), где Т₁ — минимальная допустимая температура в градусах Кельвина. В условиях теплового баланса эти мощности должны быть равны.

Режим максимального тепловыделения соответствует максимальной температуре аппаратуры. В этом случае WS₁ + N₂ = sT⁴₂ (S₁ + S₂),.

Используя два полученных уравнения, получаем:

1. Запустите программу MathCad.

2. Введите значения известных величин, присвоив их переменным с соответствующими именами. Вместо нижних индексов используйте просто дополнительную цифру в названии переменной.

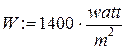
N1:= 75×watt N2:= 200×watt,

T1:= (20 + 273)×K T2:= (30 + 273)×K.

3. Обозначения физических единиц присоединяйте к соответствующим значениям через знак умножения. Если нужное обозначение неизвестно, используйте команду Insert > Unit (Вставка > Единица измерения). Измеряемая величина выбирается в списке Dimension (Размерность), а нужная единица измерения — в списке Unit (Единица измерения).

4. Присвойте переменной s значение постоянной Стефана-Больцмана

.

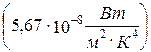Чтобы ввести греческую букву, используйте панель инструментов Greek (греческий алфавит) или введите соответствующую латинскую букву (в данном случае «s») и сразу же нажмите комбинацию клавиш CTRL+G. Так как специальной единицы для размерности этой константы не существует, ее следует составить из стандартных единиц методом умножения и деления.

5. Введите полученные в ходе анализа формулы для вычисления площадей отверстий, присвоив полученные значения переменным S₁и S₂.

6. Чтобы увидеть результаты вычислений, введите имя первой из рассчитанных переменных и нажмите клавишу [=]. Затем проделайте то же самое со второй переменной.

S1 = 0.5679 m² S2 = 1.514 m²

7. Изменение значений параметров, заданных в условии задачи, приводит к автоматическому перерасчету формул. В частности, исследуйте, изменяя значение переменной W, как изменяются требования к такому методу терморегуляции при удалении аппарата от Солнца и приближении к нему (на орбите Венеры 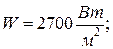на орбите Марса ).

8. Обратите внимание, что результат содержит единицы измерения в соответствии с системой единиц СИ. Используемая система единиц отображается в диалоговом окне Insert Unit (Вставка единиц измерения).

9. Чтобы изменить используемую систему единиц, дайте команду Math > Options (Математика > Параметры) и в открывшемся диалоговом окне Math Options (Параметры расчета) выберите вкладку Unit System (Система единиц). Выберите систему CGS и посмотрите, как изменились результаты (они теперь выражаются в квадратных сантиметрах). Если выбрать американскую систему единиц (U.S.), то результат будет выражен в квадратных футах.

Мы научились производить вычисления с использованием реальных размерных физических величин, а также производить преобразование данных из одной системы единиц в другую. Это позволяет немедленно получать результат в наиболее удобной форме.

Упражнение 18.3. Векторы и матрицы

Задача. Разложить вектор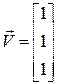

по нормированным собственным векторам матрицы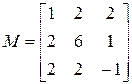

Анализ. Первый этап решения задачи состоит в нахождении собственных значений и собственных векторов данной матрицы. Затем необходимо найти вектор Т, такой что S×T = V, где S — матрица, столбцы которой представляют собой собственные вектора матрицы М.

1. Запустите программу MathCad.

2. Создайте матрицу М. Начните запись оператора присваивания, а для ввода правой части нажмите комбинацию клавиш CTRL+M, воспользуйтесь командой Insert > Matrix (Вставка > Матрица) или щелкните на кнопке Matrix or Vector (Матрица или вектор) на панели инструментов Matrix (Матрица).

3. В открывшемся диалоговом окне Insert Matrix (Вставка матрицы) укажите число строк и столбцов (по три) и щелкните на кнопке ОК.

4. Введите значения элементов матрицы в отведенные места.

5. Аналогичным образом сформируйте вектор V. Он будет представлять собой матрицу, имеющую только один столбец.

6. Собственные значения квадратной матрицы можно получить при помощи функции eigenvals. Результатом ее работы является вектор собственных значений, присвойте его переменной L.

7. Функция eigenvec позволяет получить собственный вектор, соответствующий данному собственному значению. Ей нужны два параметра: матрица, для которой ищется собственный вектор, и собственное значение, которому он соответствует. Чтобы записать собственные вектора в качестве столбцов матрицы S, надо при воить вычисленное значение столбцу матрицы. Столбцы матрицы в программе MathCad выбираются специальным верхним индексом, заключенным в угловые скобки. Чтобы ввести номер столбца, нажмите комбинацию клавиш CTRL+6 или щелкните на кнопке Matrix Column (Столбец) на панели инструментов Matrix (Матрица), после чего введите номер нужного столбца матрицы. Будьте внимательны — столбцы и строки матрицы нумеруются начиная с нуля.

S^<0>

8. В правой части оператора присваивания надо указать собственное значение матрицы. Собственные значения являются элементами вектора L. Номер элемента указывается как нижний индекс. Для ввода нижнего индекса нажмите клавишу [ или воспользуйтесь кнопкой Subscript (Индекс) на панели инструмен тов Matrix. Итоговый оператор для первого собственного вектора будет выглядеть следующим образом:

^S<0>:= eigenvec(M,L₀).

Аналогично задайте операторы для второго и третьего собственных значений.

9. Для нахождения коэффициентов при собственных векторах в разложении необходимо решить систему линейных уравнений. Ее удобно записать в матричной форме. Создайте вектор Тс тремя элементами. Величины этих элементов значения не имеют.

10.Запишите ключевое слово given.

11.Ниже запишите матричное уравнение S- Т= V. Знак логического равенства введите с помощью комбинации клавиш CTRL+=.

12.Найдите коэффициенты в разложении при помощи функции find.

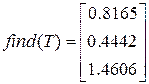
Мы научились производить операции с векторами и матрицами, использовать соответствующие функции, выделять столбцы матриц и отдельные элементы. Матричная запись часто позволяет представить задачу в более удобной форме.

Упражнение 18.4. Аналитические вычисления

Задача 1. На приведенной схеме сопротивление RR является переменным. Определить, как меняется ток между точками Л и В в зависимости от величины этого сопротивления.

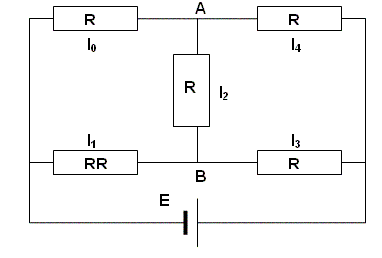
Анализ. Перенумеровав сопротивления в указанном порядке и воспользовавшись законами Кирхгофа, получим систему уравнений, позволяющую найти величины токов.

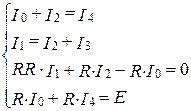
Эту систему надо решить, не подставляя конкретных значений вместо параметров R, RR и Е.

1. Запустите программу MathCad.

2. Введите ключевое слово given.

3. Введите уравнения системы, полученной в ходе анализа. Обозначьте неизвестные
токи переменными I0, I1, I2, I3, I4. Фиксированное сопротивление R обозначьте
переменной R0. Обратите внимание, что присваивать начальные значения токов
или задавать значения переменных R0, RR и E не требуется.

4. Введите функцию find, перечислив в качестве параметров неизвестные I0, I1, 12, I3, I4. Затем введите оператор аналитического вычисления, который выглядит как стрелка, направленная вправо, и вводится комбинацией клавиш CTRL+. Или кнопкой Evaluate Symbolically (Вычислить аналитически) на панели инструментов Evaluation (Вычисление).

5. Щелкните за пределами данного блока, и программа MathCad произведет аналитическое решение системы уравнений.

Полученный результат позволяет провести полный анализ схемы.

Задача 2. Найти все корни уравнения:

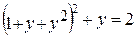
Анализ. Это уравнение четвертого порядка. Легко подобрать один корень (у = 1). Остающееся уравнение третьего порядка не имеет рациональных корней, так что поиск других корней этого уравнения — дело непростое. Неясно даже, сколько еще действительных корней имеет данное уравнение. Результаты численного решения зависят от подбора начального приближения и поэтому не гарантируют отыскания всех корней уравнения. Мы же решим это уравнение аналитически.

6. Введите заданное уравнение. Чтобы раскрыть скобки, дайте команду Symbolics > Simplify (Аналитические вычисления > Упростить).

7. Выделите в полученном уравнении независимую переменную (в данном случае у) и дайте команду Symbolics > Variable > Solve (Аналитические вычисления > Переменная > Решить).

Программа MathCad выдаст вектор, элементами которого являются корни данного уравнения.

8. Полученный результат содержит сложные комплексные радикалы, и его невозможно применить с пользой (нельзя даже точно сказать, являются ли корни действительными или комплексными). Чтобы разделить действительную и мнимую части, выделите результат вычисления целиком и дайте команду
Symbolics > Evaluate > Complex (Аналитические вычисления > Вычислить > В комплексном виде). В результате запись станет более простой, но результат все-таки останется трудным для восприятия.

9. Следующий шаг — раскрытие скобок, в данном случае упрощение аргументов тригонометрических функций. Для этого примените команду Symbolics > Expand (Аналитические вычисления >Раскрыть). Только теперь станет ясно, что все корни уравнения действительные (все мнимые компоненты сократятся). Это наилучшая точная запись решения, которую можно получить с помощью программы MathCad.

10.Чтобы получить результат в числовом виде, достаточно ввести в конце выражения (итогового или на любой из предыдущих стадий) команду вычисления (=).

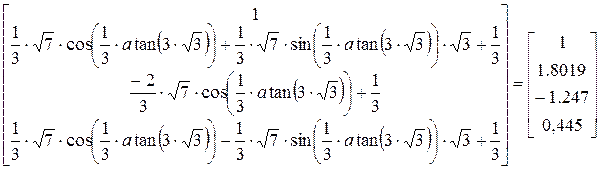
Мы научились использовать программу MathCad для выполнения аналитических вычислений. Это позволяет получать точные решения задач, содержащих переменные параметры, анализировать полученные результаты, а также получать полный набор решений для некоторых типов уравнений.

Упражнение 18.5. Анализ результатов испытаний

Задача. К пружине последовательно подвешивали грузы массой 1, 2, 3,..., 20 кг. В результате был получен список величин удлинения пружины (в миллиметрах). Определить основные статистические параметры полученного набора измерений. Рассчитать жесткость пружины и массу узла, использованного для крепления грузов к пружине, воспользовавшись методом наименьших квадратов.

Таблица измерений:

Вес, кг
Растяжение, мм	3,4	6,8	9,1	12,2	13,4	17,2	22,1	24,2	27,8	29,5	31,7	37,6	39,5	42,8	45,5	46,5	52,1	52,4	56,6	62,4

Анализ. Для решения этой задачи достаточно использовать стандартные средства статистических вычислений, имеющиеся в программе MathCad. Теоретически, растяжение пружины определяется формулой k×x = (m + m₀)×g. Если определить статистическими методами коэффициенты a и b вуравнении

х = a×m + b, то получим:

1. Запустите программу MathCad.

2. Введите таблицу данных, предназначенных для статистического анализа, как матрицу с двумя столбцами, первый из которых содержит веса грузов, а второй — значения растяжения пружины.

3. Определите число точек в наборах данных с помощью функции rows.

п:= rows(data) n = 20.

4. Вычислите среднее растяжение пружины в ходе эксперимента с помощью функции mean.

Y:=data^<1>mean(Y) = 31.645.

5. Вычислите медиану значений растяжения пружины при помощи функции median.

median(Y) = 30.6.

6. Вычислите среднеквадратичное отклонение и дисперсию величины растяжения пружины при помощи функции stdev.

stdev(Y) = 17.4041, stdev(Y)² = 302.9025.

7. Определите коэффициенты линейного уравнения являющегося наилучшим приближением для данных наборов данных. Функция slope позволяет вычислить коэффициент наклона прямой, а функция intercept — свободный член.

X:=data^<0>

b₀:= intercept(X,Y) b ₀ = 0.0132

V=slope(X,Y) b₁ = 3.0126

8. Определите жесткость пружины:

k = 7.448-10⁵(Н/м).

9. Определите массу узла крепления:

т = 4.3677 (г). 10.

10.Сохраните созданный документ для использования в следующем упражнении.

Мы научились применять функции, используемые для статистического анализа данных. Программа MathCad содержит и другие функции аналогичного назначения, которые можно использовать для интерполяции и экстраполяции данных, а также их сглаживания.

Упражнение 18.6. Построение графиков

Задача. Используя результаты, полученные в предыдущем упражнении, построить график, отображающий экспериментальные данные и аппроксимирующую зависимость. Построить другой график, отображающий величину отклонения экспериментальных значений от аппроксимирующей прямой.

Анализ. Для построения графика можно использовать функцию, заданную набором данных или формулой. Формулы для функций, полученных в результате проделанных расчетов, необходимо определить, прежде чем их можно будет использовать при построении графика.

1. Запустите программу MathCad.

2. Загрузите документ, созданный в предыдущем упражнении.

3. Переместите точку ввода в нижнюю часть документа.

4. Запишите формулу функции r (х) для определения координат точек, лежащих на аппроксимирующей прямой. Коэффициенты соответствующего уравнения были получены в предыдущем упражнении.

r(х):= b₀ + b₁×x.

5. Нажмите клавишу [@], щелкните на кнопке X-Y Plot (Декартовы координаты) на панели инструментов Graph (График) или дайте команду Insert >Graph > X-Y Plot (Вставка > График > Декартовы координаты). В документе появится область для создания графика.

6. Вместо заполнителя в нижней части графика укажите в качестве независимой переменной первый столбец матрицы data (data^<0> или X).

7. Вместо заполнителя слева от графика укажите, что по вертикальной оси должны откладываться значения из второго столбца матрицы data и определенная выше линейная функция г(х). В качестве разделителя используется запятая. Диапазон значений для осей координат выбирается программой MathCad автоматически.

8. Чтобы изменить вид автоматически построенного графика, дважды щелкните внутри него. Откроется диалоговое окно Formatting Currently Selected X-Y Plot (Форматирование графика в декартовых координатах). Первая запись в списке на вкладке Traces (Кривые) соответствует первой отображенной кривой. Для изменения записи используются поля под списком.

Рис. 18.4. Задание способа отображения линий графика

9. Под столбцом Legend Label (Подпись) введите название графика.

10.В раскрывающемся списке под столбцом Symbol (Маркер) выберите способ обозначения для отдельных точек.

11.Под столбцом Туре (Вид линии) укажите, что необходимо пометить отдельные точки (points), а не провести непрерывную линию.

12.Выберите в списке вторую кривую и настройте ее отображение по своему вкусу.

13.Установите флажок Hide Arguments (Скрыть параметры), чтобы не отображать названия осей.

14.Сбросьте флажок Hide Legend (Скрыть подписи), чтобы включить отображение под графиком заданных подписей кривых.

15.В поле Title (Заголовок) на вкладке Labels (Надписи) задайте название графика и включите режим его отображения: флажок Show Title (Показать заголовок).

Рис. 18.5. График экспериментальных точек и аппроксимирующей

прямой

16. Постройте график, на котором отображалась бы величина отклонения точек от линии приближения (b₀ + b₁×X – Y)._× Отформатируйте его, используя те же средства, что и в предыдущем случае.

Заголовок и подписи, использующие русские буквы, могут отображаться неправильно. Коррекцию обеспечивает выбор шрифта, правильно воспроизводящего кириллицу. Дайте команду Format > Equation (Формат > Выражение), в раскрывающемся списке Style Name (Имя стиля) выберите пункт Variables (Переменные) и щелкните на кнопке Modify (Изменить). Для задания шрифта используйте поле со списком Шрифт.

Упражнение 18.7. Построение трехмерных графиков

Задача. Изобразить на графике приблизительную форму электронных облаков в атомах.

Анализ. По современным представлениям электронные уровни в атоме определяются четырьмя квантовыми числами. Форма электронного облака определяется двумя из этих чисел:

• число l определяет тип орбитали (значения 0-3 соответствуют s-, p-, d- и f - орбиталям);

• число т определяет магнитный момент электрона и может изменяться в диапазоне от - l до l.

При т= 0 форма электронного облака определяется на основе многочленов Лежандра первого рода: 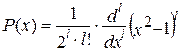, где l -степень многочлена.

В этом случае

Параметрическое задание соответствующей поверхности имеет следующий вид:

Углы q, f изменяются в диапазоне от 0 до 2p.

1.Запустите программу MathCad.

2.Определите переменную /, которая укажет тип орбитали.

l:=3

3. Построение поверхности будем производить по точкам. Задайте два диапазона, которые будут определять изменение параметров q, f, задающих поверхность. Удобно определить границы диапазона в целых числах (через точку с запятой, на экране изображаются две точки), а затем произвести перемасштабирование на отрезок [0; 2p].

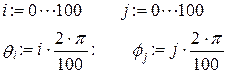
4. Определите двумерные матрицы, определяющие значения координат х, у и z в зависимости от значения параметров. Используйте названия переменных

X0, Y0, Z0.

5. Дайте команду Insert > Graph > Surface Plot (Вставка > График > Поверхность) или воспользуйтесь кнопкой Surface Plot (Поверхность) на панели инструментов Graph (График).

Рис. 18.6. Трехмерное изображение электронной f-орбитали

6. В появившейся области графика вместо заполнителя укажите имена отображаемых матриц через запятую, заключив все их в скобки: (XO,YO,ZO).

7. Чтобы изменить формат построенного графика, дважды щелкните на его области. Откроется диалоговое окно 3-D Plot Format (Формат трехмерного графика).

8. На вкладке General (Общие) установите флажок Equal Scales (Равный масштаб), чтобы обеспечить одинаковый масштаб по осям координат.

9. На вкладке Appearance (Оформление) установите переключатель Fill Surface (Заливка поверхности), чтобы обеспечить заливку построенной поверхности.

10.На вкладке Lighting (Подсветка) включите режим освещения поверхности. Установите флажок Enable Lighting (Включить подсветку), отключите все источники света, кроме первого.

11.На панели Light Location (Размещение источника) задайте координаты источника света. Используйте кнопку Применить, чтобы сразу видеть последствия сделанных настроек. По окончании настройки закройте диалоговое окно щелчком на кнопке ОК.

12.Путем протягивания мыши в области графика измените направление осей координат, чтобы изображение было видно наиболее отчетливо.

13.Изменяя значение l, можно увидеть форму электронных облаков для разных орбиталей, в том числе и не встречающихся в природе.

Мы научились строить трехмерные графики с изображением объемных поверхностей, заданных параметрически. Это фактически означает умение изображать любые фигуры, которые могут потребоваться в ходе практической работы.

Упражнение 18.8. Решение дифференциальных уравнений

Задача. Найти функцию у(х), удовлетворяющую дифференциальному уравнению

и имеющую значение 0 при х = 0.

Анализ. Это простое дифференциальное уравнение допускает точное аналитическое решение, однако в данном упражнении предполагается использование стандартной функции программы MathCad, осуществляющей численное решение данного уравнения. Результат вычислений можно после этого сравнить с точным решением.

1. Запустите программу MathCad.

2. Задайте начальное значение функции как элемент вектора у, размерность которого соответствует числу решаемых уравнений (в данном случае единице): у₀:= 0.

3. Создайте функцию Т(х, у}, которая вычисляет значение производной при заданных значениях независимой переменной и неизвестной функции:

Т(х,у):= - y₀ + x×cos(x).

4. Определите начальное (точка 0) и конечное значение отрезка интегрирования.

а:= 0, b := 12 ×p.

5. Укажите число шагов интегрирования.

К:= 20.

6. Вычислите численное решение уравнения при помощи функции rkfixed.

Z:= rkfixed (y,a,b,K,T).

Рис. 18.7. Графики численного и точного решения дифференциального уравнения

Результат вычислений — матрица Z с двумя столбцами, первый из которых содержит значения независимой переменной, а второй — соответствующие значения функции.

7.Постройте график полученного решения.

8.Определите аналитическое решение данного уравнения при тех же начальных условиях.

9.Нанесите аналитическую кривую на тот же график и сравните поведение численного и точного решения.

10. Измените число шагов, на которые делится отрезок интегрирования, и исследуйте, как изменяется результат расчета при уменьшении и увеличении этого параметра.

Мы научились численно решать дифференциальные уравнения первого порядка с помощью программы MathCad. Использованный метод без изменений переносится на системы, содержащие два или большее число дифференциальных уравнений. Увеличение величины шага интегрирования ускоряет получение результата, но снижает его точность. При слишком большой величине шага результат расчетов может вообще не соответствовать реальному решению.

Глава 19 Публикация WEB-документов

Размещение собственных материалов в Интернете включает два этапа: подготовку материалов и их публикацию. Подготовка материалов состоит в создании документов, имеющих формат, принятый в Интернете, то есть, Web-страниц, написанных на языке HTML Публикация материалов, то есть открытие к ним доступа, осуществляется после решения организационных вопросов, связанных с получением дискового пространства на Web-сервере для их размещения.

Дата добавления: 2014-12-26