На использовании интеграла Дюамеля

Расчет переходного процесса методом, основанным

Отклик цепи на произвольное воздействие , являющееся непрерывной функцией времени, можно определить с помощью интеграла Дюамеля:

(5.43)

где – начальное значение воздействия;

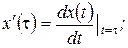
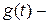переходная функция; 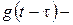переходная функция, в которой t заменено на .

Переходной функцией 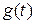является реакция цепи при подключении ее в момент времени 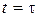к источнику единичного напряжения или тока, называемого единичной функцией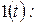

Таким образом, зная отклик цепи 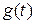на единичную функцию с помощью интеграла Дюамеля (5.43), можно найти отклик цепи на произвольное воздействие .

Если воздействующая функция имеет различные выражения на разных интервалах времени и имеет или нет скачки, то интервал интегрирования разбивается на отдельные участки, а реакция цепи записывается для отдельных интервалов времени [4]. Например, для функции, изображенной на рисунке 5.16, интервал интегрирования разбивается на три участка.

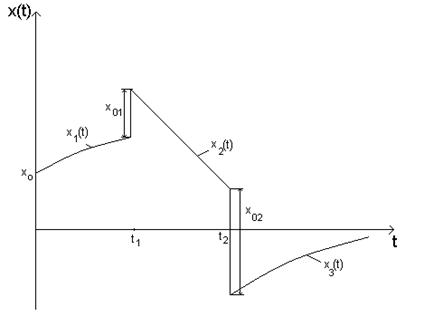
Рис. 5.16. Входное воздействие сложной формы

На первом участке от 0 до (не включая скачок ) получим:

На участке от до (не включая скачок ) реакция цепи будет иметь вид:

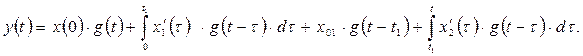Слагаемое 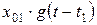обусловлено положительным скачком входного воздействия в момент времени .

На третьем участке от до реакция цепи определяется следующим образом:

Слагаемое 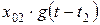обусловлено отрицательным скачком воздействия в момент времени .

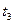Метод интеграла Дюамеля можно использовать для определения отклика цепи на произвольное воздействие и в случае, когда известна реакция этой цепи на действие единичного импульса тока или напряжения, называемого дельта-функцией. Дельта-функция характеризует собой единичный импульс и определяется следующими равенствами:

Реакция цепи на действие дельта-функции называется импульсной характеристикой 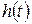. Импульсная характеристика связана с переходной функцией 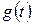следующим соотношением:

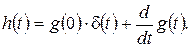
Реакция цепи на произвольное воздействие по известной импульсной характеристике 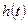определяется по формуле:

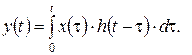(5.44)

При расчетах необходимо учитывать основные свойства дельта-функции:

5.3.1 Пример расчёта переходного процесса в цепи методом,

Дата добавления: 2014-12-26