Проведение испытаний и подсчет результатов

При проведении лабораторной работы записывается машинная диаграмма растяжения в координатах F-∆L. На рис. 2.2 показаны характерные диаграммы растяжения малоуглеродистых сталей. По диаграмме можно определить следующие механические характеристики материалов:

А. Характеристики прочности: 1. Предел пропорциональности σ_пц – наибольшее нормальное напряжение, до которого материал следует закону Гука

, (2.1)

где F_пц – нагрузка, соответствующая пределу пропорциональности, Н;

б

а

в

Рис. 2.2. Диаграммы растяжения:

а – имеющая «зуб» текучести; б – имеющая резкий переход из упругой области

деформирования в пластическую; в – имеющая плавный переход из упругой области

деформирования в пластическую

А ₀ – начальная площадь поперечного сечения образца диаметром d ₀, мм².

Значение F_пц определяется по диаграмме растяжения как ордината точки П, расположенной на верхнем конце наклонной прямой участка диаграммы. Приближенно положение этой точки на диаграмме находится с помощью линейки, прикладываемой к начальному участку диаграммы растяжения. Более точный метод определения F_пц требует применения специальных приборов для измерения деформаций (тензометров) и приводится в ГОСТ 1497-84;

2. Предел текучести σ_Т – напряжение, соответствующее текучести

, (2.2)

где F_Т – нагрузка, соответствующая площадке текучести (ордината точки В, рис. 2.2, б).

Условный предел текучести σ _0,2 (см. рис. 2.2, в)

, (2.3)

где F _0,2 – нагрузка, при которой относительная остаточная деформация

% = 0,2 %,

где L ₀ – первоначальная длина расчетной части образца.

Для определения нагрузки F _0,2 на диаграмме растяжения по оси ∆L (см. рис. 2.2, в) откладывают в масштабе величину ∆L_0,2 = 0,2 % и через эту точку проводят прямую, параллельную начальному участку диаграммы, до пересечения ее с кривой деформации в точке В.

Если диаграмма имеет «зуб» текучести, то определяются верхний и нижний пределы текучести

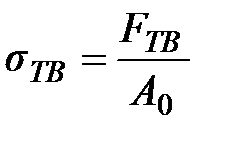и , (2.4)

где F_тви F_тн – верхняя величина пика нагрузки и наименьшая величина нагрузки при течении материала без учета переходного эффекта;

3. Предел прочности материала (временное сопротивление) σ_В

, (2.5)

где F_max – максимальная нагрузка (ордината точки С, см. рис. 2.2).

Напряжение σ_В считается условным, поскольку оно вычисляется по отношению к начальной площади поперечного сечения образца А ₀, которая в действительности при деформировании уменьшается. Для σ_пц и σ_т это уменьшение незначительно, поэтому условность характеристик обычно не оговаривается.

4. Напряжение S_к, соответствующее разрыву образца (истинное сопротивление разрыву)

, (2.6)

где F_к – нагрузка при разрыве образца (ордината точки Д, см. рис. 2),

А_к – площадь поперечного сечения разрушенного образца в месте разрыва (на рис. 1, б диаметр шейки обозначен d_к).

У пластичных материалов всегда S_к > σ_В.

Все вычисленные механические характеристики прочности округляются до 0,5 Н/мм².

Б. Характеристики пластичности: 1. Относительное остаточное удлинение d (строчная греческая «дельта»)

%, (2.7)

где L_к – конечная длина расчетной части разрушенного образца;

2. Относительное остаточное сужение y (строчная греческая «пси»)

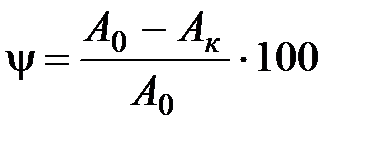%. (2.8)

Величины δ и ψ характеризуют пластичность материала при растяжении, т.е. его способность получать остаточные деформации до разрушения. Вычисленные значения округляются до 0,5 %.

Рассмотрим поведение материала при разгрузке и последующем вторичном нагружении. Если нагрузить образец до некоторого значения F_м > F_Т (см. рис. 2, а) и затем его разгрузить, то на диаграмме растяжения получим прямую М-1, параллельную начальному (упругому) участку О-П. При разгрузке материал ведет себя как упругий (закон разгрузки). При новом нагружении график деформирования повторяет линию нагрузки 1-М (закон вторичного нагружения), а затем описывает оставшийся участок МСД диаграммы растяжения. Повышение предела пропорциональности в результате предварительной остаточной деформации называется наклепом.

Дата добавления: 2014-12-26