
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод сильной связи
|
|
|
|
Зонная структура углеродных нанотрубок
Исследования дисперсионных свойств углеродных наноматериалов достаточно удобно проводить в рамках метода сильной связи, который хорошо зарекомендовал себя в расчетах систем из легких атомов.
Вследствие трансляционной симметрии кристалла в направлении векторов решетки 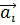 любая волновая функция в кристалле должна удовлетворять теореме Блоха
любая волновая функция в кристалле должна удовлетворять теореме Блоха
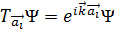 , (i = 1, 2, 3) (1)
, (i = 1, 2, 3) (1)
где 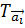 – трансляционная операция вдоль вектора решетки, а
– трансляционная операция вдоль вектора решетки, а 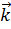 - волновой вектор. Волновая функция Ψ может быть разложена различными способами. Этот метод имеет определенные преимущества (они просто интегрируемы (иногда и аналитически), точность зависит только от числа использованных плоских волн), но и не лишен недостатков: 1) большой масштаб вычислений, 2) достаточно сложно соотнести плоскую волну и атомную орбиталь в кристалле. Другая форма Ψ, которая удовлетворяет теореме Блоха (1) — линейная комбинация атомных орбиталей (ЛКАО) (в элементарной ячейке или в атоме). Т.е., базисные функции представляются в виде:
- волновой вектор. Волновая функция Ψ может быть разложена различными способами. Этот метод имеет определенные преимущества (они просто интегрируемы (иногда и аналитически), точность зависит только от числа использованных плоских волн), но и не лишен недостатков: 1) большой масштаб вычислений, 2) достаточно сложно соотнести плоскую волну и атомную орбиталь в кристалле. Другая форма Ψ, которая удовлетворяет теореме Блоха (1) — линейная комбинация атомных орбиталей (ЛКАО) (в элементарной ячейке или в атоме). Т.е., базисные функции представляются в виде: 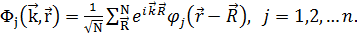
Здесь j – индекс атомной орбитали, 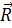 – позиция элементарной ячейки, количество волновых функций в элементарной ячейке обозначается как n, что приводит к наличию n волновых функций в кристалле для заданного
– позиция элементарной ячейки, количество волновых функций в элементарной ячейке обозначается как n, что приводит к наличию n волновых функций в кристалле для заданного 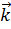 . N – число элементарных ячеек. Элементарные ячейки взвешиваются фазовым коэффициентом
. N – число элементарных ячеек. Элементарные ячейки взвешиваются фазовым коэффициентом 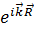 . Преимущества данного метода для углеродных структур заключаются в том, что он позволяет: 1) вывести формулы физических свойств, 2) хорошо подходит для легких атомов, 3) число базисных функций n может быть небольшим.
. Преимущества данного метода для углеродных структур заключаются в том, что он позволяет: 1) вывести формулы физических свойств, 2) хорошо подходит для легких атомов, 3) число базисных функций n может быть небольшим.
Можно получить квантование вектора 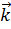 в зоне Бриллюэна
в зоне Бриллюэна 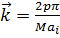 , p = 0, 1, … M–1. M =
, p = 0, 1, … M–1. M = 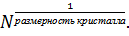
Собственные функции твердого тела описываются линейной комбинацией (ЛК) базисных функций 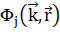 :
: 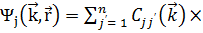
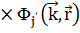 .
.
Поскольку 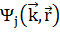 должны удовлетворять блоховской теореме (1) суммирование проводится только для одних и тех же
должны удовлетворять блоховской теореме (1) суммирование проводится только для одних и тех же 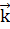 . Собственные значения для состояний j даются формулой:
. Собственные значения для состояний j даются формулой:
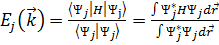 , (2)
, (2)
где H – гамильтониан в твердом теле. Подставляя (1) в (2) получим: 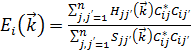 , где
, где 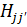 и
и 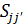 называются матрицами переноса и перекрытия соответственно. Минимизацией энергии можно вывести т. н. секулярное уравнение: det[H – ES] = 0, решение которого и дает дисперсионное соотношение.
называются матрицами переноса и перекрытия соответственно. Минимизацией энергии можно вывести т. н. секулярное уравнение: det[H – ES] = 0, решение которого и дает дисперсионное соотношение.
Таким образом, алгоритм метода сильной связи выглядит следующим образом.
1. Выбрать элементарную ячейку и трансляционные вектора 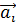 . Определить координаты атомов. Выбрать n орбиталей, которые учитываются в расчете.
. Определить координаты атомов. Выбрать n орбиталей, которые учитываются в расчете.
2. Определить зону Бриллюэна для данной элементарной ячейки и вектора обратной решетки 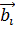 . Выбрать характерные точки и направления зоны Бриллюэна.
. Выбрать характерные точки и направления зоны Бриллюэна.
3. Для каждого k посчитать матрицы 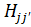 и
и 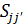 .
.
4. Решить секулярное уравнение и найти дисперсионное отношение E(k).
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 543; Нарушение авторских прав?; Мы поможем в написании вашей работы!