
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 4. Симплекс-метод с искусственным базисом
|
|
|
|
Для задачи, записанной в канонической форме задачи линейного программирования, можно непосредственно указать ее опорный план, если среди векторов Aj, компонентами которых служат коэффициенты при неизвестных в системе уравнений данной задачи, имеется m единичных. Однако для многих задач линейного программирования, записанных в канонической форме задачи линейного программирования и имеющих опорные планы, среди векторов Aj не всегда есть т единичных.
Метод искусственного базиса применяется в тех случаях, когда затруднительно найти первоначальный опорный план исходной задачи ЛП, записанной в канонической форме.
Метод искусственного базиса заключается в применении правил симплекс-метода к так называемой М-задаче. Она получается из исходной добавлением к левой части системы уравнений в канонической форме исходной ЗЛП таких искусственных единичных векторов Pi, 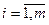 с соответствующими неотрицательными искусственными переменными si, чтобы вновь полученная матрица содержала систему единичных линейно-независимых векторов.
с соответствующими неотрицательными искусственными переменными si, чтобы вновь полученная матрица содержала систему единичных линейно-независимых векторов.
В линейную форму исходной задачи добавляется в случае ее максимизации слагаемое, представляющее собой произведение числа (-М) на сумму искусственных переменных, где М — достаточно большое положительное число. Для сравнения оценок нужно помнить, что М — достаточно большое положительное число, поэтому из базиса будут выводиться в первую очередь искусственные переменные.
В процессе решения М-задачи следует вычеркивать в симплекс-таблице искусственные векторы по мере их выхода из базиса. Если все искусственные векторы вышли из базиса, то получаем исходную задачу. Если оптимальное решение М-задачи содержит искусственные векторы или М-задача неразрешима, то исходная задача также неразрешима.
|
|
|
Пример 8. Рассмотрим ЗЛП вида:
Целевая функция
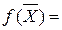

при ограничениях

Решить симплекс-методом.
Решение: Задача была решена графическим методом в примере 4. Решим и сравним результаты.
Приведем ЗЛП к канонической форме:
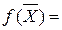

при ограничениях

Среди векторов A1, A2, A3, A4, A5, A6 нет четырех единичных вектора, необходимых для перехода к решению задачи симплекс-методом.

Поэтому в левые части 1-го и 2-го уравнений добавляем неотрицательные искусственные переменные s1 и s2, чтобы вновь полученная матрица A содержала систему единичных линейно-независимых векторов.
Получаем следующую М-задачу:

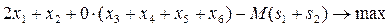
при ограничениях

Первоначальный опорный планХ=(0; 0; 0; 0; 6; 7; 4; 3), определяемый системой четырех единичных векторов P1, P2, A5 и A6. Искусственной переменной s1 соответствует единичный вектор P1, а переменной s1 вектор P2. Составляем симплексную таблицу:
 Таблица 3.9
Таблица 3.9
| I | i | Базис | Сб | B | 2 | 1 | 0 | 0 | 0 | 0 | -M | -M | Qmin |
| A1 | A2 | A3 | A4 | A5 | A6 | P1 | P2 | ||||||
| 1 | P1 | -M | -1 | -1 | 2 | ||||||||
 2 2
| P2 | -M | -1 | 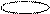 1 1
| |||||||||
| 3 | A5 | 0 | -1 | 2 | |||||||||
| 4 | A6 | 0 | 1 | ||||||||||

|  -7M -7M
| -5M-2 | -M-1 | M | M |
Как видно из табл. 3.9, план не оптимален, так как есть отрицательные оценки  , самая наименьшая из которых 5M-2, так как под М понимается достаточно большое положительное число. Вектор P2 исключаем из базиса. Этот вектор не имеет смысла вводить ни в один из последующих базисов, поэтому в дальнейшем столбец данного вектора не заполняется. Рассчитываем оценки Qmin, и переходим к новому опорному плану и строим новую симплексную таблицу:
, самая наименьшая из которых 5M-2, так как под М понимается достаточно большое положительное число. Вектор P2 исключаем из базиса. Этот вектор не имеет смысла вводить ни в один из последующих базисов, поэтому в дальнейшем столбец данного вектора не заполняется. Рассчитываем оценки Qmin, и переходим к новому опорному плану и строим новую симплексную таблицу:
 Таблица 3.10
Таблица 3.10
| II | i | Базис | Сб | B | 2 | 1 | 0 | 0 | 0 | 0 | -M | Qmin | |
| A1 | A2 | A3 | A4 | A5 | A6 | P1 | |||||||
| 1 | P1 | -M | 
| -1 | 
| 
| |||||||
| 2 | A1 | 2 | 
| 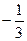
| - | ||||||||
| 3 | A5 | 0 | -3 | 3 | |||||||||
 4
4
| A6 | 0 | 
| 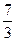
|  0
0
| ||||||||

| 2-2M | 0 | 
|  M
M
| 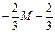
|
Из табл. 3.10 видно, что план не оптимален, одна отрицательная оценка 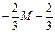 и не искусственные векторы выведены из базиса. Рассчитываем оценки Qmin и переходим к новому опорному плану и строим новую симплексную таблицу:
и не искусственные векторы выведены из базиса. Рассчитываем оценки Qmin и переходим к новому опорному плану и строим новую симплексную таблицу:
|
|
|
Таблица 3.11
| III | i | Базис | Сб | B | 2 | 1 | 0 | 0 | 0 | 0 | -M | Qmin | |
| A1 | A2 | A3 | A4 | A5 | A6 | P1 | |||||||
| 1 | P1 | -M | 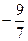
| -1 | 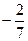
| ||||||||
| 2 | A1 | 2 | 
| 
| |||||||||
| 3 | A5 | 0 | 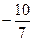
| 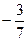
| |||||||||
| 4 | A4 | 0 | 
| 
| |||||||||

| 2-2M | 0 | 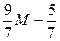
| M | 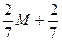
|
Так как все оценки  неотрицательны, но искусственный вектор P1 не выведен из базиса, следовательно М-задача неразрешима, что означает, что исходная задача также неразрешима, что и было также получено при ее решении графическим методом в примере 4.
неотрицательны, но искусственный вектор P1 не выведен из базиса, следовательно М-задача неразрешима, что означает, что исходная задача также неразрешима, что и было также получено при ее решении графическим методом в примере 4.
Пример 9. Рассмотрим ЗЛП вида:
Целевая функция
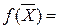

при ограничениях

Решить симплекс-методом.
Решение: В канонической форме записи целевая функция стремится к максимуму. Переход от минимуму к максимуму осуществляется по правилу:
f1(  ) = - f(
) = - f(  ).
).
А затем полученный максимум взять с противоположным знаком.
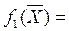

при ограничениях

Первоначальный опорный планХ=(0; 0; 2; -4; 2), определяемый системой трех единичных векторов A3, A4 и A5 не являетсядопустимым решением, так как координата x4 =-4, что является недопустимым по условию неотрицательности переменных xj 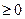 . Для того, чтобы первоначальный опорный план был допустимым решением, исистема ограничений содержала систему единичных векторов, сделаем следующие преобразования 2-го ограничения и целевой функции:
. Для того, чтобы первоначальный опорный план был допустимым решением, исистема ограничений содержала систему единичных векторов, сделаем следующие преобразования 2-го ограничения и целевой функции:



Первоначальный опорный планХ=(0; 0; 2; 0; 2; 4), определяемый системой трех единичных векторов A3, P1 и A5. Составляем симплексную таблицу:
 Таблица 3.12
Таблица 3.12
| i | Базис | Сб | B | -1 | -5 | 0 | 0 | 0 | -M | Qmin | |
| A1 | A2 | A3 | A4 | A5 | P1 | ||||||
| I | 1 | A3 | -0 | -2 |  - -
| ||||||
 2 2
| P1 | -M | -1 | 
| |||||||
| 3 | A5 | 0 | -2 | 2 | |||||||

| -4M | 1-2M | 5-3M | 0 | M |  0 0
| |||||
| II |  1
1
| A3 | 0 | 
| 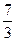
| 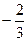
| 2 | ||||
| 2 | A2 | -5 | 
| 
| 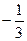
| 2 | |||||
| 3 | A5 | 0 | 
| 
| 
| - | |||||

| 
|  
| 
| ||||||||
| III | 1 | A1 | -1 | 
| 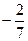
| ||||||
| 2 | A2 | -5 | 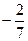
| 
| |||||||
| 3 | A5 | 0 | 
| 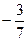
| |||||||

| -2 |
|
|
|
Значение f1(  )=F0= -1·2+0·0=-2, полученный результат возьмем с противоволожным знаком f1(
)=F0= -1·2+0·0=-2, полученный результат возьмем с противоволожным знаком f1(  ) = - f(
) = - f(  )=2- минимум функции иоптимальный план Х=(2; 0; 0; 0; 6).
)=2- минимум функции иоптимальный план Х=(2; 0; 0; 0; 6).
Пример 10. Рассмотрим ЗЛП вида:
Целевая функция

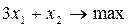
при ограничениях

Решить симплекс-методом.
Решение: Приведем ЗЛП к канонической форме записи:
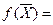

при ограничениях

Составляем симплексные таблицы итераций:
Таблица 3.13
| i | Базис | Сб | B | 3 | 1 | 0 | 0 | 0 | -M | Qmin | |
| A1 | A2 | A3 | A4 | A5 | P1 | ||||||
| I |  1 1
| P1 | -M | -1 | -1 |  1 1
| |||||
| 2 | A4 | 0 | 5 | ||||||||
| 3 | A5 | 0 | -2 | 4 | |||||||

| -M | M-3 | -1-M | M | 0 |  0 0
| |||||
| II | 1 | A2 | 1 | -1 | -1 | - | |||||
 2 2
| A4 | 0 | 3 | ||||||||
| 3 | A5 | 0 | -1 | - | |||||||

|  -4 -4
| -1 | |||||||||
| III | 1 | A2 | 1 | 
| 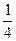
| ||||||
| 2 | A1 | 3 | 
| 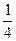
| |||||||
| 3 | A5 | 0 | 
| 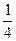
| |||||||

| 13 |
Значение F0= 3·3+1·4=13, максимум функции иоптимальный план Х= (3; 4; 0; 0; 6).
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 1198; Нарушение авторских прав?; Мы поможем в написании вашей работы!