Введение. Варианты индивидуальных заданий 18

Варианты индивидуальных заданий 18

Библиографический список 24

Целью настоящих методических указаний является помощь студентам – заочникам в выполнении контрольной работы №1.

Перед выполнением контрольной работы студент должен изучить соответствующие разделы рекомендуемой литературы [1] – [3] и воспользоваться решениями типовых примеров, содержащихся в настоящих методических указаниях. Большое количество образцов решенных задач дано в руководстве к решению задач [5]. Задачи для самостоятельного решения имеются как в представленных методических указаниях, так и в сборниках задач [4], [6].

Номер варианта по каждому заданию студент выбирает по формуле ,

где - номер варианта,

-номер задания,

-предпоследняя цифра шифра студента,

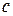-последняя цифра шифра.

Пример.

Пусть шифр студента 1235, тогда:

номер варианта первого задания: = ;

номер варианта второго задания: ;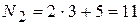

номер варианта третьего задания: ;

номер варианта четвертого задания: .

Таким образом, студент, имеющий шифр 1235 должен решать задачу №8 в первом задании, №11 – во втором, №14 – в третьем, №17 – в четвертом.

Если итоговая цифра по формуле получится число больше 20, то для определения варианта от полученной цифры отнимают 20.

Пример.

Пусть шифр студента 1298.

Номер варианта второго задания: . Промежуток 26-20=6. Таким образом, во втором задании студент решает задачу вариант №6.
1 Решение систем линейных уравнений методами Крамера и Гаусса

Пусть дана система n уравнений с n неизвестными:

Основная матрица А такой системы квадратная. Определитель этой матрицы

называется определителем системы.

Если определитель системы отличен от нуля, то система называется невырожденной и имеет единственное решение.

В дальнейшем мы будем иметь дело только с такими системами.

Наиболее простым методом для решения таких систем линейных уравнений является метод Крамера.

Формулы Крамера имеют вид:

(1.1.1)

Более универсальным и эффективным является метод Гаусса, состоящий в последовательном исключении неизвестных.

Решение осуществляется в два этапа: 1) система приводится к треугольному виду, 2) последовательно определяют неизвестные .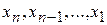

Пример 1.

Решить систему уравнений методами Крамера и Гаусса:

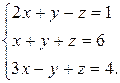
Решение:

а) Метод Крамера.

Найдем определитель системы 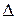, 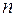. Предварительно сложив второй столбец с третьим и разложив определитель по элементам последнего столбца.

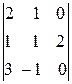= =2(-1) 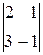=-2(-2-3)=10 .

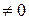Так как 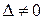, то система имеет единственное решение.

Найдем определител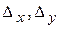и и 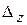, заменив в матрице коэффициентов соответственно первый, второй, третий столбцы столбцом свободных членов (при вычислении определителя 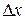преобразования аналогичные предыдущему.)

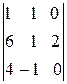= =2(-1) -2(-1-4)=10.

При вычислении определителя 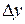последнюю строку складываем с первой и вычитаем из второй строки. Разлагаем по элементам последнего столбца.

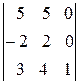= =1(-1)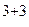 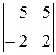=10+10=20.

При вычислении определителя 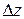последнюю строку складываем с первой и со второй строки и разлагаем получившийся определитель по элементам второго столбца.

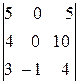= =-1(-1)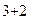 =50-20=30.

Подставляя найденные значения в формулы (1.1.1), получим:

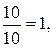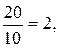х= у= z=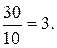

б) Метод Гаусса.

Составим расширенную матрицу системы:

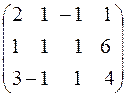
Разрешающим элементом удобно иметь единицу, поэтому переставим второе уравнение на место первого.

Получим нули в первом столбце, умножив первое уравнение последовательно на (-2) и (-3) и складывая со вторым и третьим.

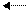
(-2) (-3)

С помощью второго элемента второй строки сделаем нуль во втором столбце третьей строки, для чего умножим вторую строку на (-2) и сложим с третьей.

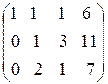(-2) .

Таким образом, свели матрицу к треугольному виду. Запишем полученную систему уравнений:

Из последнего уравнения сразу находим значение z=3, подставляя которое во второе уравнение находим у=11-3z=11-9=2. Затем из первого уравнения найдем

х=1, у=2, z=3.

Дата добавления: 2014-12-26