Векторная диаграмма трансформатора

Приведение параметров вторичной обмотки и схема замещения приведенного трансформатора

В общем случае параметры первичной обмотки трансформатора отличаются от параметров вторичной обмотки. Эта разница наиболее ощутима при больших коэффициентах трансформации, что затрудняет расчеты и построение векторных диаграмм, так как в этом случае векторы электрических величин первичной обмотки значительно отличаются по своей длине от одноименных векторов вторичной обмотки. Указанные затруднения устраняются приведением всех параметров трансформатора к одинаковому числу витков, обычно к числу витков первичной обмотки w₁. С этой целью все величины, характеризующие вторичную цепь трансформатора, — ЭДС, напряжение, ток и сопротивления — пересчитывают на число витков w₁ первичной обмотки.

Таким образом, вместо реального трансформатора с коэффициентом трансформации k = w₁/w₂ получают эквивалентный трансформатор с k=w ₁/ w’ ₂ = 1, где w’ ₂ =w ₁. Такой трансформатор называют приведенным. Однако приведение вторичных параметров трансформатора не должно отразиться на его энергетических показателях: все мощности и фазовые сдвиги во вторичной обмотке приведенного трансформатора должны остаться такими, как и в реальном трансформаторе.

Так, электромагнитная мощность вторичной обмотки реального трансформатора Е₂I₂ должна быть равна электромагнитной мощности вторичной обмотки приведенного трансформатора:

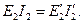(1.27)

Подставив значение приведенного тока вторичной обмотки I ₂= I ₂(w ₂/ w ₁,) в (1.27), получим формулу приведенной вторичной ЭДС:

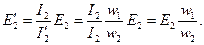(1.28)

Так как U ₂ I ₂ ≈ U’ ₂ I’ ₂, то приведенное напряжение вторичной обмотки

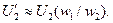(1.29)

Из условия равенства потерь в активном сопротивлении вторичной обмотки имеем . Определим приведенное активное сопротивление:

(1.30)

Приведенное индуктивное сопротивление рассеяния вторичной обмотки определяют из условия равенства реактивных мощностей ,откуда

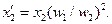(1.31)

Приведенное полное сопротивление вторичной обмотки трансформатора

(1.32)

Приведенное полное сопротивление нагрузки, подключенной на выводы вторичной обмотки, определим по аналогии с (1.32):

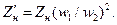(1.33)

Уравнения напряжений и токов для приведенного трансформатора имеют вид

(1.34)

Эти уравнения устанавливают аналитическую связь между параметрами трансформатора во всем диапазоне нагрузок от режима х.х. до номинальной.

Еще одним средством, облегчающим исследование электромагнитных процессов и расчет трансформаторов, является применение электрической схемы замещения приведенного трансформатора. На рис. 1.18, а представлена эквивалентная схема приведенного трансформатора, на которой сопротивления r и х условно вынесены из соответствующих обмоток и включены последовательно им. Как было установлено ранее, в приведенном трансформаторе k = 1, а поэтому . В результате точки А и а, атакже точки X и х на схеме имеют одинаковые потенциалы, что позволяет электрически соединить указанные точки, получив Т–образную схему замещения приведенного трансформатора (рис. 1.18, б). В электрической схеме замещения трансформатора магнитная связь между цепями заменена электрической.

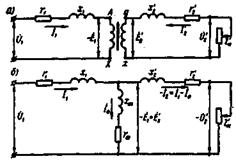
Рис. 1.18. Эквивалентная схема (в) и схема замещения (б) приведенного

Схема замещения приведенного трансформатора удовлетворяет всем уравнениям ЭДС и токов приведенного трансформатора (1.34) и представляет собой совокупность трех ветвей: первичной — сопротивлением Z ₁ = r ₁ + jx₁ и током ; намагничивающей — сопротивлением Z_m=r_m+jx_m и током ; вторичной — с двумя сопротивлениями: сопротивлением собственно вторичной ветви Z'₂ = r’₂ + jx'₂ и сопротивлением нагрузки Z'_H = r _н' ± jx'_H и током . Изменением сопротивления нагрузки Z'_H на схеме замещения могут быть воспроизведены все режимы работы трансформатора.

Параметры ветви намагничивания Z_m = r_m + jx_m определяются током х.х. Наличие в этой ветви активной составляющей r_m обусловлено магнитными потерями в трансформаторе (см. § 1.14).

Все параметры схемы замещения, за исключением Z'_H, являются постоянными для данного трансформатора и могут быть определены из опыта х.х. и опыта к.з. (см. §1.11).

Воспользовавшись схемой замещения приведенного трансформатора и основными уравнениями напряжений и токов (1.34), построим векторную диаграмму трансформатора, наглядно показывающую соотношения и фазовые сдвиги между токами, ЭДС и напряжениями трансформатора. Векторная диаграмма — графическое выражение основных уравнений приведенного трансформатора (1.34).

Построение диаграммы (рис. 1.19, а) следует начинать с вектора максимального значения основного магнитного потока .

Вектор тока опережает по фазе вектор потока на угол δ, а векторы ЭДС 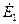, и отстают от этого вектора на угол 90° [см. (1.6) и (1.7)]. Далее строим вектор 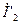. Для определения угла сдвига фаз между и 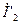следует знать характер нагрузки. Предположим, что нагрузка трансформатора активно-индуктивная. Тогда вектор 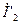. отстает по фазе от на угол

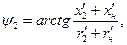(1.35)

определяемый как характером внешней нагрузки, так и собственными сопротивлениями вторичной обмотки.

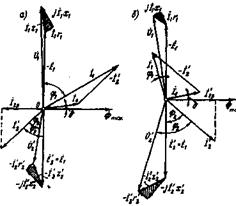
Рис. 1.19. Векторные диаграммы трансформатора при активно-индуктивной (а) и активно-емкостной (б) нагрузках

Для построения вектора вторичного напряжения 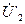необходимо из вектора ЭДС вычесть векторы падений напряжения и 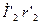. С этой целью из конца вектора опускаем перпендикуляр на направление вектора тока 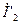и откладываем на нем вектор 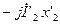. Затем проводим прямую, параллельную 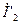, и на ней откладываем вектор 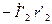. Построив вектор 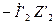, получим треугольник внутренних падений напряжения во вторичной цепи. Затем из точки О проводим вектор 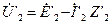, который опережает по фазе ток 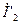на угол φ₂=arctg(х’_н/r_н').

Вектор первичного тока строим как векторную сумму: 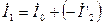. Вектор проводим из конца вектора противоположно вектору 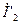. Построим вектор 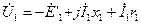, для чего к вектору 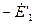, опережающему по фазе вектор потока 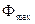на 90°, прибавляем векторы внутренних падений напряжения первичной обмотки: вектор 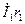, параллельный току , и вектор 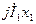, опережающий вектор тока на угол 90°. Соединив точку О с концом вектора 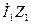, получим вектор , который опережает по фазе вектор тока , на угол φ₁.

Иногда векторную диаграмму трансформатора строят с целью определения ЭДС обмоток. В этом случае заданными являются параметры вторичной обмотки: U₂, I₂ и соsφ₂. Зная w₁/w₂, определяют 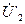и 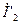а затем строят векторы этих величин под фазовым углом φ₂ друг к другу. Вектор ЭДС 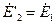получают геометрическим сложением вектора напряжения 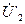с падениями напряжения во вторичной обмотке:

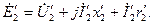
В случае активно-емкостной нагрузки векторная диа­грамма трансформатора имеет вид, показанный на рис. 1.19, б. Порядок построения диаграммы остается прежним, но вид ее несколько изменяется. Ток 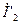в этом случае опережает по фазе ЭДС на угол

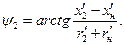(1.36)

При значительной емкостной составляющей нагрузки падение напряжения в емкостной составляющей сопротивления нагрузки и индуктивное падение напряжения рассеяния во вторичной обмотке частично компенсируют друг друга. В результате напряжение 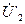может оказаться больше, чем ЭДС . Кроме того, реактивная (опережающая) составляющая вторичного тока 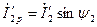совпадает по фазе с реактивной составляющей тока х.х. 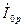, т. е. оказывает на магнитопровод трансформатора подмагничшающее действие.

Это ведет к уменьшению первичного тока , по сравнению с его значением при активно-индуктивной нагрузке, когда составляющая 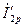оказывает размагничивающее влияние (рис. 1.19, а).

Дата добавления: 2014-12-27