Группы соединения обмоток

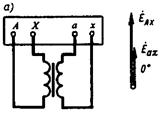
Рис. 2.1. Группы соединения обмоток однофазных трансформаторов:

а — группа I/I — 0; б — группа I/I — 6

До сих пор при построении векторных диаграмм трансформатора считалось, что ЭДС фазы обмотки ВН 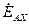и обмотки НН 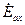совпадают по фазе. Но это справедливо лишь при условии намотки первичной и вторичной обмоток трансформатора в одном направлении и одноименной маркировке выводов этих обмоток, как показано на рис.2.1, а. Если же в трансформаторе изменить направление обмотки НН или же переставить обозначения ее выводов, то ЭДС 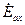окажется сдвинутой по фазе относительно ЭДС 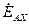на 180° (рис. 2.1, б). Сдвиг фаз между ЭДС 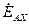и 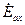принято выражать группой соединения. Так как этот сдвиг фаз может изменяться от 0 до 360°, а кратность сдвига составляет 30°, то для обозначения группы соединения принят ряд чисел: 1, 2, 3, 4, 5, 6, 7,8,9, 10, 11 и 0.

Угол смещения вектора линейной ЭДС обмотки НН по отношению к вектору линейной ЭДС обмотки ВН определяют умножением числа, обозначающего группу соединения, на 30°. Угол смещения отсчитывают от вектора ЭДС обмотки ВН по часовой стрелке до вектора ЭДС обмотки НН. Например, группа соединения 5 указывает, что вектор ЭДС НН отстает по фазе от вектора ЭДС ВН на угол 5·30° = 150°.

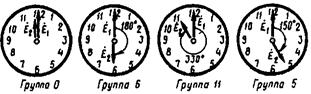
Рис. 2.2. Сравнение положения стрелок часов с обозначением групп соединения

Для лучшего понимания принятого обозначения групп соединения пользуются сравнением с часами. При этом вектор ЭДС обмотки ВН соответствует минутной стрелке, установленной на цифре 12, а вектор ЭДС обмотки НН — часовой стрелке (рис.2.2). Так же необходимо иметь в виду, что совпадение по фазе векторов ЭДС 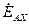и 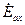, эквивалентное совпадению стрелок часов на циферблате, обозначается группой 0 (а не 12). Кроме того, следует помнить, что за положительное направление вращения векторов ЭДС принято их вращение против часовой стрелки.

Таким образом, в однофазном трансформаторе возможны лишь две группы соединения: группа 0, соответствующая совпадению по фазе 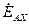и 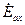, и группа 6, соответствующая сдвигу фаз между 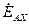и 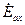на 180°. Из этих групп ГОСТ предусматривает лишь группу 0, она обозначается I/I—0.

Применением разных способов соединения обмоток в трехфазных трансформаторах можно создать 12 различных групп соединения. Рассмотрим в качестве примера схему соединений «звезда—звезда» (рис. 2.3, а). Векторные диаграммы ЭДС показывают, что сдвиг между линейными ЭДС и в данном случае равен нулю. В этом можно убедиться, совместив точки А и а при наложении векторных диаграмм ЭДС обмоток ВН и НН. Сле­довательно, при указанных схемах соединения обмоток имеет место группа 0; обозначается Y/Y—0. Если же на стороне НН в нулевую точку соединить зажимы а, b и с, а снимать ЭДС с зажимов х, у и z, то ЭДС изменит фазу на 180°и трансформатор будет принадлежать группе 6 (Y/Y—6) (рис.2.3, б).

При соединении обмоток «звезда—треугольник», показанном на рис. 2.4, а, имеет место группа 11 (Y/∆—11). Если же поменять местами начала и концы фазных обмоток НН, то вектор повернется на 180° и трансформатор будет относиться к группе 5 (Y/∆—5) (рис. 2.4, б).

При одинаковых схемах соединения обмоток ВН и НН, например Y/Y и ∆/∆, получают четные группы соединения, а при 62 неодинаковых схемах, например Y/∆ или ∆/Y, — нечетные.

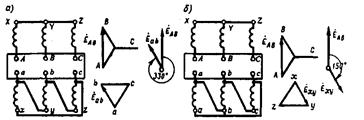
Рис. 2.4. Схемы соединения обмоток и векторные диаграммы: а — для группы Y/Д—11; б — для группы Y/Д—5

Рассмотренные четыре группы соединения (0, 6, 11 и 5) называют основными. Из каждой основной группы соединения методом круговой перемаркировки выводов на одной стороне трансформатора, например на стороне НН (без изменения схемы соединения), можно получить по две производные группы. Например, если в трансформаторе с группой соединения Y/Y—0 (рис. 2.3, а) выводы обмотки НН перемаркировать и вместо последовательности аbс принять последовательность саb, то вектор ЭДС повернется на 120°, при этом получим группу соединения Y/Y—4. Если же выводы обмоток НН перемаркировать в последовательность bса, то вектор Е_аЬ повернется еще на 120°, а всего на 240°; получим группу Y/Y—8.

Аналогично от основной группы 6 путем круговой перемаркировки получают производные группы 10 и 2, от основной группы I/I — производные группы 3 и 7, от основной группы 5 — производные группы 9 и 1.

Основные группы соединения имеют некоторое преимущество перед производными, так как предусматривают одноименную маркировку выводов обмоток, расположенных на одном стержне. Это уменьшает вероятность ошибочных присоединений. Однако не все группы соединения имеют практическое применение в трехфазных трансформаторах. ГОСТ определяет схемы и группы соединения, применяемые для силовых двухобмоточных трансформаторов общепромышленного назначения (рис. 2.5).

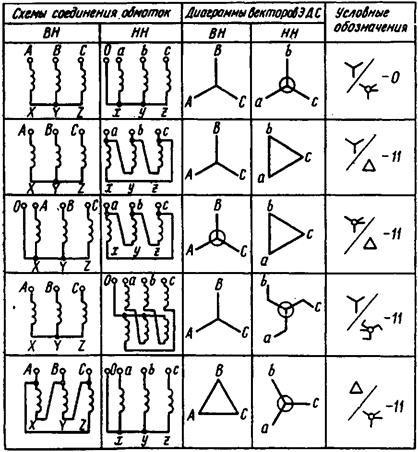
Рис. 2.5. Схемы и группы соединения обмоток трехфазных двухобмоточных

трансформаторов

Соединяя обмотки НН в зигзаг в сочетании с соединением обмотки ВН в звезду или треугольник, можно получить практически любой угол сдвига фаз между ЭДС обмоток ВН и НН. Этого достигают разделением обмотки НН на две части (см. § 1.11) с различным соотношением витков в этих частях, а следовательно, и с различным значением угла β (см. рис. 1.22, б).

При изготовлении или в процессе эксплуатации трансформаторов иногда возникает необходимость в опытной проверке группы соединения. Существует несколько методов такой проверки, но наиболее распространены методы фазометра и вольтметра.

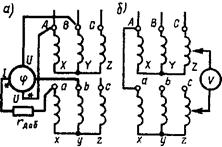
Рис. 2.6. Проверка группы соединения Y/Y—0 методами фазометра (а) и вольтметра (б)

Метод фазометра. Основан на непосредственном измерении угла фазового сдвига между соответствующими линейными напряжениями (ЭДС) обмоток ВН и НН с помощью фазометра φ, включенного по схеме, показанной на рис. 2.6, а. Параллельную обмотку фазометра U—U подключают к стороне ВН, а последовательную обмотку 1—1 — к стороне НН. Для ограничения тока в последовательной обмотке ее подключают через добавочное сопротивление г_доб.. Затем трансформатор включают в сеть с симметричным трехфазным напряжением. Для удобства измерений желательно, чтобы фазометр имел полную (360°) шкалу.

Метод вольтметра. Непосредственного измерения угла фазового сдвига между линейными напряжениями (ЭДС) этот метод не дает. Это косвенный метод и основан на измерении вольтметром напряжений (ЭДС) между одноименными выводами обмоток ВН и НН. Если проверяют группу соединения Y /Y— О (рис. 2.6, б), то, соединив проводом выводы А и а, измеряют напряжение Uь-в (между выводами bи В) и U_c-С (между выводами с и С). Если предполагаемая группа соединения Y/Y—0 соответствует фактической, то напряжение (В)

где k_л =U_АВ/U_ab — отношение линейных напряжений (ЭДС) ВН и НН, т, е. коэффициент трансформации линейных напряжений (ЭДС),

Если проверяют группы соединения 6, 11 или 5, то для проверки измеренных значений напряжений пользуются формулами:

группа Y/Y—6

(2-2)

группа Y/D — 11

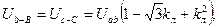(2.3)

группа Y/D —5

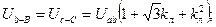(2.4)

Здесь U_аЬ и U_xy— линейные напряжения на выводах обмоток НН, В.

Если условия равенства напряжений по приводимым формулам не соблюдаются, то это свидетельствует о нарушениях в маркировке выводов трансформатора.

Дата добавления: 2014-12-27