Рекомендации по организации практической работы

Главная задача для учащихся на минимальном уровне изучения данной темы: научиться основным методам организации расчетов с помощью электронных таблиц. Для этого они должны освоить следующие практические приемы работы в среде электронной таблицы:

• осуществлять перемещение табличного курсора; устанавливать курсор в нужную ячейку;

• вводить данные: числа, тексты, формулы;

• редактировать данные в ячейках;

• копировать информацию в ячейках;

• вставлять и удалять строки и столбцы.

Теоретические вопросы, которые на первом этапе вызывают наибольшие затруднения — это правила записи формул и понимание принципа относительной адресации. Их отработку следует проводить на задачах и упражнениях. Основные правила записи формул сводятся к следующему:

• все символы в формуле записываются в одну строчку;

• проставляются все знаки операций (в отличие от алгебры, где знак умножения часто пропускается);

• используются круглые скобки для влияния на последовательность выполнения операций;

• учитываются приоритеты операций, расположенные в таком порядке: ^Л — возведение в степень; *, / — умножение и деление; +, — — сложение и вычитание;

• приоритет стандартных функций выше арифметических операций; аргумент записывается в круглых скобках после имени функции;

• последовательно записанные операции одинакового старшинства выполняются в порядке записи, т. е. слева направо (возведение в степень — справа налево).

Все эти правила совпадают с правилами записи выражений в языках программирования. Поэтому при более позднем изучении программирования этот вопрос ученикам будет уже знаком.

Для упражнений на данную тему следует давать задачи как прямые (дано математическое выражение, записать формулу для электронной таблицы), так и обратные (дана формула, записать математическое выражение).

Например, дано математическое выражение:

Нужно записать формулу для электронной таблицы. Во-первых, переменным величинам в этой формуле нужно поставить в соответствие адреса ячеек. Например так: х — А1, у — В1. Теперь записать формулу:

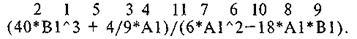
Для обоснования правильности формулы следует пронумеровать операции в порядке их выполнения так, как это сделано в примере.

Пример обратной задачи. Дана формула для электронной таблицы:

Нужно записать соответствующее математическое выражение. От адресов ячеек перейдем к математическим переменным: С5 — х, В5 — у, А5 — z, B2 — k. Следующим шагом нужно, как это делали раньше, указать последовательность вычислений:

Теперь становится ясно, что эта формула соответствует следующему математическому выражению:

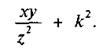
Теперь о принципе относительной адресации. Как уже отмечалось, это один из базовых принципов функционирования электронной таблицы. Адреса ячеек, используемых в формулах, определяются относительно места расположения формулы. Смысл этого принципа следует пояснить на примерах. В данной ниже таблице формулу в ячейке С1 табличный процессор воспринимает так: сложить значение из ячейки, расположенной на две клетки левее, со значением из ячейки, расположенной на одну клетку левее данной формулы.

	А	В	С
			А1 + В1

При переносе этой формулы в любую другую ячейку любым способом (копированием, вследствие вставки или удаления фрагментов) сохранится сформулированный выше смысл формулы. Вследствие этого изменятся ссылки на ячейки. Например, при копировании формулы из ячейки С1 в ячейку С2 формула примет вид: А2 + В2. При копировании в ячейку F6 примет вид: F4 + F5.

Для закрепления понимания принципа относительной адресации следует выполнить несколько заданий. Условия предлагаемых

задач должны быть следующего типа: дан фрагмент электронной таблицы (например такой, как приведен выше). Какие формулы занесутся в ячейки блока D1:F1, если в них скопировать формулу из ячейки С2? Результат выполнения этого задания в режиме отображения формул и в режиме отображения значений будет следующим (табл. 12.5):

Таблица 12.5

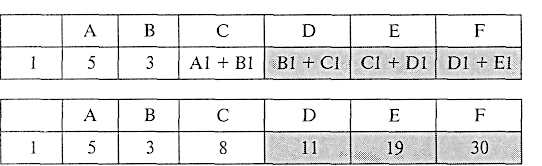
Здесь заливкой отмечены ячейки, в которые произведено копирование.

Наиболее эффективной будет такая постановка задания: сначала решить задачу теоретически, а затем проверить полученное решение на компьютере. В этом случае происходит как закрепление понимания теоретического вопроса, так и отработка навыков копирования данных в электронной таблице.

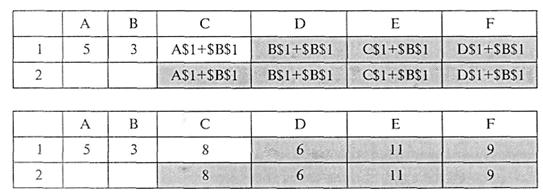
При знакомстве с приемом «замораживания» адресов ячеек в формулах полезно выполнить аналогичные упражнения. Например, в той же таблице в ячейке С1 записана формула: А$1+$В$1. Какой вид примет формула, если ее скопировать в блок Dl:F1 и в блок С2: F2? Результаты решения этой задачи будут следующими (табл. 12.6):

Таблица 12.6

Основные типы расчетных задач, которые учащиеся должны научиться решать на электронных таблицах:

1) получение несложных расчетных ведомостей;

2) статистическая обработка числовых таблиц;

3) построение диаграмм по табличным данным;

4) сортировка таблицы по значениям параметра (столбца);

5) табулирование функций.

Рассмотрим основные методические проблемы, возникающие при решении задач первого типа на примере следующего задания: построить таблицу расчета ежемесячной оплаты за расход электроэнергии по данным показаниям счетчика и стоимости 1 кВт-ч.

Начать решение задачи следует с проектирования таблицы. Это наиболее сложный этап для учеников. Во-первых, необходимо пояснить алгоритм подсчета оплаты за электричество (не всем ученикам это очевидно). Показания счетчика снимаются в конце каждого месяца. Расход электроэнергии за месяц определяется как разность между показаниями счетчика в данном месяце и в предыдущем. Затем оплата подсчитывается как произведение расхода на цену 1 кВт-ч. Для расчета платы за январь необходимо знать показания счетчика в декабре прошлого года. Из всего сказанного нужно сделать вывод: какие величины являются исходными данными, какие — вычисляемыми по формулам. Исходные данные — показания счетчика каждый месяц и стоимость 1 кВт-ч, а вычисляемые — ежемесячный расход электроэнергии и сумма оплаты.

Теперь можно переходить к построению таблицы. Следует сразу же сформулировать ученикам некоторые правила оформления таблицы. Во-первых, у таблицы обязательно должен быть заголовок. Строки и столбцы таблицы должны быть поименованы. Постепенно учитель должен познакомить учеников с основными средствами форматирования таблицы для получения оформленного документа. Начальная часть таблицы будет выглядеть так (предполагается, что цена 1кВт-ч равна 20 коп., а плата подсчитывается в руб., табл. 12.7):

Таблица 12.7

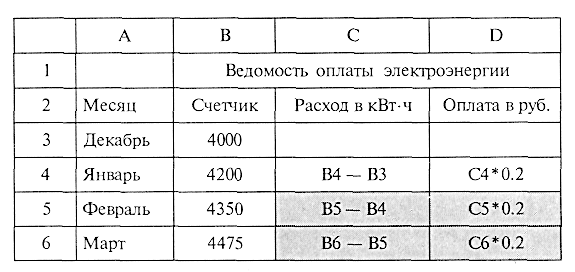
Во время работы с табличным процессором обязательно нужно использовать прием копирования формул. Формулы в ячейках С4, D4 являются исходными. Все формулы, расположенные ниже, получены путем копирования. Из этого примера ученикам станет ясен практический смысл принципа относительной адресации: он позволяет быстро создавать большие таблицы без переписывания формул.

Разбор этой задачи приводит к идее использования абсолютного (замороженного) адреса. Удобно цену 1 кВт-ч хранить в отдельной ячейке (например, в В16), а в ячейке D4 записать формулу С4*$В$16. При копировании формулы абсолютный адрес меняться не будет. Теперь, если произойдет изменение цены 1 кВт-ч, то будет достаточно внести изменения лишь в одну ячейку В16.

Очень часто в числовых таблицах подсчитываются различные итоговые данные: суммы, средние значения, наибольшие и наименьшие значения. Получение таких данных называется статистической обработкой таблицы. Во всех табличных процессорах имеются для этого соответствующие функции. В задачах того же типа, что рассмотрена выше, следует добавить задание на подобную статистическую обработку данных. Например, к таблице оплаты электроэнергии добавить вычисление общей суммы денег, выплаченных за год, среднемесячного расхода электроэнергии, наибольшей и наименьшей месячной платы.

Представление табличных данных в графической форме часто используется на практике. Графическая обработка придает наглядность, обозримость результатам расчетов. Табличные процессоры предоставляют пользователю на выбор множество типов диаграмм (гистограмм, графиков). Такие графические средства принято называть деловой графикой.

Для построения диаграммы пользователь должен указать ее тип и сообщить табличному процессору, из каких блоков таблицы нужно выбирать всю необходимую информацию. Достаточно подробно основные типы диаграмм описаны в [3], даны рекомендации по их применению.

Большие возможности придает использование в электронной таблице условной и логических функций. Таблица без использования условной функции реализует в себе линейный вычислительный алгоритм. Использование условной функции вносит в таблицу структуру ветвления. Потребность в ветвлении появляется при усложнении условия задачи. Например, если бы правило оплаты за электроэнергию звучало так: за первые 100 кВт-ч нужно платить по 20 коп.; за каждый 1 кВт-ч, израсходованный выше этого, нужно платить по 30 коп. Тогда расчетная формула в ячейке D4 выглядела бы так:

IF(C4<=100, С4*0.2, 20+(С4 - 100)*0.3)

Возможность сортировки данных в таблице существует у табличных процессоров благодаря наличию режима базы данных. Обычно сортировка организуется в выделенном блоке таблицы. Как и в базах данных, указывается столбец, по которому производится сортировка и порядок сортировки: по возрастанию или по убыванию значений в столбце. Например, в рассмотренной таблице можно отсортировать строки, начиная с четвертой, по убыванию размера оплаты. Тогда вначале расположится самый «дорогой» месяц, далее — по убыванию.

Табулирование функции — одна из часто решаемых прикладных задач математики. Табулирование означает построение таблицы значений функции для значений аргумента, изменяющихся в определенном интервале с данным шагом. Табулирование позволяет исследовать функцию: проследить характер изменения, выделить области корней, определить экстремальные значения. Применяя прием копирования, в электронной таблице можно быстро построить таблицу значений функции большого размера. Для этого достаточно ввести две начальные строки таблицы и затем скопировать их вниз на нужное число строк. Например, таблица функции

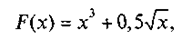
вычисленной с шагом 0,2 начиная от значения х = 0, строится следующим образом (табл. 12.8):

Таблица 12.8

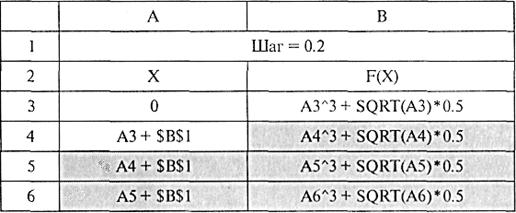
Если нужно изменить начальное значение X в таблице, то достаточно исправить ячейку A3, а для изменения шага нужно изменить содержимое ячейки В1. Формулы записываются по правилам, принятым в используемом табличном процессоре.

Применение электронных таблиц для решения задач математического моделирования описывается в подразделе 1.0.4.

Дата добавления: 2014-12-27