Drawbacks of Bisection Method

Advantages of Bisection Method

a) The bisection method is always convergent. Since the method brackets the root, the method is guaranteed to converge.

b) As iterations are conducted, the interval gets halved. So one can guarantee the error in the solution of the equation.

a) The convergence of bisection method is slow as it is simply based on halving the interval.

b) If one of the initial guesses is closer to the root, it will take larger number of iterations to reach the root.

c) If a function 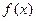is such that it just touches the x -axis (Figure 6) such as

it will be unable to find the lower guess, 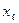, and upper guess, 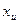, such that

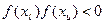
d) For functions 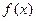where there is a singularity[1] and it reverses sign at the singularity, bisection method may converge on the singularity (Figure 7).

An example include

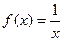
and 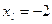, 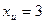are valid initial guesses which satisfy

.

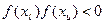However, the function is not continuous and the theorem that a root exists is also not applicable.

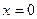Figure 6: Function has a single root at that cannot be bracketed.

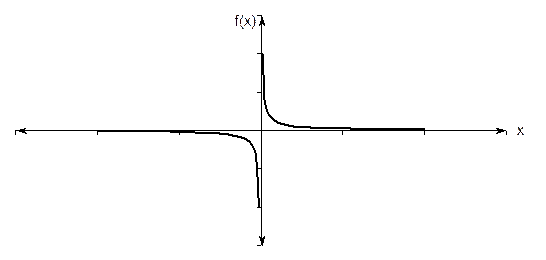
Figure 7: Function 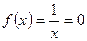has no root but changes sign.

NONLINEAR EQUATIONS
Topic	Bisection Method of Solving Nonlinear Equations
Summary	These are textbook notes of bisection method of finding roots of nonlinear equation, including convergence and pitfalls.
Major	General Engineering
Authors	Autar Kaw
Date	December 26, 2014
Web Site	http://numericalmethods.eng.usf.edu

[1] A singularity in a function is defined as a point where the function becomes infinite. For example, for a function such as 1/x, the point of singularity is x=0 as it becomes infinite.

Дата добавления: 2014-12-27