Динамика материальной точки. Инерциальные системы отсчета и первый закон Ньютона

Связь между линейными и угловыми величинами, характеризующими движение

Отдельные точки вращающегося тела имеют различные линейные скорости v, которые непрерывно изменяют свое направление и зависят от угловой скорости ω и расстояния r соответствующей точки до оси вращения. Точка, находящаяся на расстоянии r от оси вращения проходит путь ΔS = rΔφ. Поделим обе части равенства на

Переходя к пределам при 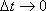, получим 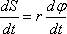или .

Таким образом, чем дальше отстоит точка от оси вращения, тем больше ее линейная скорость. По определению ускорения, или

что значения линейной скорости, тангенциального и нормального ускорений растут по мере удаления от оси вращения. Формула устанавливает связь между модулями векторов v, r, ω, которые перпендикулярны друг к другу.

Динамика изучает движение тела в связи с теми причинами (взаимодействиями между телами), которые обуславливают тот или иной характер движения.

В основе классической (ньютоновской) механики лежат три закона динамики, сформулированные Ньютоном в 1687 г. Эти законы возникли как результат обобщения большого количества опытных фактов.

Инерциальные системы отсчета и первый закон Ньютона:

Формулировка первого закона Ньютона такова: всякое тело находится в состоянии покоя или равномерного и прямо­линейного движения, пока воздействие со стороны других тел не заставит его изменить это состояние. Оба названных состояния отличаются тем, что ускорение тела равно нулю. Поэтому формулировке первого закона можно придать следующий вид: скорость любого тела остается постоянной, пока воздействие на это тело других тел не вызовет ее изменения.

Первый закон Ньютона выполняется не во всякой системе отсчета. Рассмотрим две системы отсчета, движущиеся друг относительно друга с некоторым ускорением. Если относительно одной из них тело покоится, то относительно другой оно, очевидно, будет двигаться с ускорением. Следовательно, первый закон Ньютона не может выполняться одновременно в обеих системах.

Система отсчета, в которой выполняется первый закон Ньютона, называется инерциальной, поэтому первый закон называют иногда законом инерции. Система отсчета, в которой первый закон Ньютона не выполняется, называется неинерциальной системой отсчета. Инерциальных систем существует бесконечное множество. Любая система отсчета, движущаяся относительно некоторой инерциальной системы прямолинейно и равномерно, будет также инерциальной.

Опытным путем установлено, что система отсчета, центр которой совмещен с Солнцем, а оси направлены на соответствующим образом выбранные звезды, является инерциальной. Эта система называется гелиоцентрической (гелиос - по-гречески солнце). Любая система отсчета, движущаяся равномерно и прямолинейно относительно гелиоцентрической системы, будет инерциальной.

Земля движется относительно Солнца и звезд по криволинейной траектории, имеющей форму эллипса. Криволинейное движение всегда происходит с некоторым ускорением. Кроме того, Земля совершает вращение вокруг своей оси. По этим причинам система отсчета, связанная с земной поверхностью, движется с ускорением относительно гелиоцентрической системы отсчета и не является инерциальной. Однако ускорение такой системы настолько мало, что в большом числе случаев ее можно считать практически инерциальной. Но иногда неинерциальность системы отсчета, связанной с Землей, оказывает существенное влияние на характер рассматриваемых относительно нее механических явлений.

Дата добавления: 2015-04-24