Векторные диаграммы для представления гармонических колебаний

Векторные диаграммы для представления гармонических колебаний. Дифференциальное уравнение гармонических колебаний. Энергия колебательного движения.

Скорость и ускорение при гармонических колебаниях.

Колебания, при которых изменения физических величин происходят по закону косинуса или синуса (гармоническому закону), наз. гармоническими колебаниями.

Согласно определению скорости, скорость – это производная от координаты по времени.

Согласно определению ускорения, ускорение – это производная от скорости по времени:

Колебаниями называются движения или процессы, которые характеризуются определенной повторяемостью во времени.

Гармонические колебания - колебания, при которых колеблющаяся величина изменятся со временем по закону синуса (косинуса).

Гармонические колебания описываются уравнением типа:

x = A cos (₀ t +),

где

x – смещение колеблющейся точки от положения равновесия.

А - максимальное значение колеблющейся величины, называемое амплитудой колебания,

0 - круговая (циклическая) частота,

 - начальная фаза колебания в момент времени t=0,

(₀ t +) - фаза колебания в момент времени t.

Гармонические колебания изображаются графически методом вращающегося вектора амплитуды, или методом векторных диаграмм.

Для этого из произвольной точки О, выбранной на оси x под углом ,равнымначальной фазе колебания, откладывается вектор А, модуль которого равен амплитуде А рассматриваемого колебания.

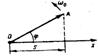
Если этот вектор привести во вращение с угловой скоростью ₀, равной циклической частоте колебаний, то проекция конца вектора будет перемещаться по оси x и принимать значения от - А до + А, а колеблющаяся величина будет изменяться со временем по закону s = A cos (₀ t +). Таким образом, гармоническое колебание можно представить проекцией на некоторую произвольно выбранную ось вектора амплитуды А, отложенного из произвольной точки оси под углом , равным начальной фазе, и вращающегося с угловой скоростью ₀ вокруг этой точки.

Дата добавления: 2015-04-24