Теорема Гаусса. Независимость потока от поверхности. Доказательство теоремы

Независимость потока от поверхности. Покажем, что и для поверхности любой другой формы, если она замкнута и заключает внутри себя точечный заряд q, поток вектора Е также будет равен . Для поверхности, не имеющей «морщин» (рис. 10,а), это утверждение очевидно. Действительно, такая поверхность, как и поверхность сферы, пересекается каждой

Рис. 10.

линией Е только один раз. Поэтому число пересечений равно количеству линий, выходящих из заряда, т. е. . При вычислении потока через поверхность с «морщинами» (на рис. 10,6 показана только одна из линий Е) нужно учесть, что число пересечений данной линии с поверхностью может быть в рассматриваемом случае только нечетным, причем эти пересечения будут вносить в общий поток попеременно то положительный, то отрицательный вклад. То есть, сколько бы раз данная линия не пересекала поверхность, результирующий вклад в поток будет равен либо плюс единице (для линии, выходящей в конечном счете наружу), либо минус единице (для линии, входящей внутрь). Таким образом, какова бы ни была форма замкнутой поверхности, охватывающей точечный заряд q, поток вектора Е сквозь эту поверхность оказывается равным .

Пусть внутри некоторой замкнутой поверхности заключено несколько точечных зарядов произвольных знаков: q ₁, q ₂ и т. д. Поток вектора Е по определению равен

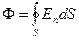(16)

(кружок у знака интеграла указывает на то, что интегрирование производится по замкнутой поверхности). В силу принципа суперпозиции полей

(17)

Подставив (17) в выражение для потока, получим

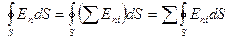
где 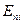– нормальная составляющая напряженности поля, создаваемого i-м зарядом в отдельности. Последняя перестановка операции суммирования и интегрирования возможна, так как i относится к нумерации зарядов, интегрирование ведется по произвольной поверхности.

Выше было показано:

Следовательно,

(18)

Это утверждение носит название теоремы Гаусса. Теорема может быть сформулирована следующим образом: поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на e ₀.

Рис. 11.

В частности, если внутри поверхности заряды отсутствуют, поток равен нулю. В этом случае каждая линия напряженности поля (создаваемого зарядами, расположенными вне поверхности) пересекает поверхность четное число раз, выходя наружу столько же раз, сколько и входя внутрь (рис. 11). В итоге вклад, вносимый в поток каждой из линий, будет равен нулю. Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью r, теорема Гаусса должна быть записана следующим образом:

(19)

где интеграл справа берется по объему V, охватываемому поверхностью S.

Дата добавления: 2015-04-24